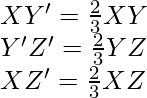Soluciones NCERT Clase 10 – Capítulo 11 Construcciones – Ejercicio 11.1

Posted on by Rudeus Greyrat

En cada uno de los siguientes, proporcione también la justificación de la construcción:

Pregunta 1. Dibuja un segmento de recta de 7,6 cm de longitud y divídelo en la proporción 5:8. Mide las dos partes .

Solución:

Pasos de construcción:

Para dividir el segmento de línea de 7,6 cm en la proporción de 5: 8.

Paso 1. Dibuja un segmento de recta AB de 7,6 cm de longitud.

Paso 2. Dibuja un rayo AC que forme un ángulo agudo con el segmento de línea AB.

Paso 3. Marque los puntos = 13 como (5+8=13) puntos, como A 1 , A 2 , A 3 , A 4 …….. A 13 , en el rayo AC tal que se convierte en AA 1 = A 1 A 2 = A 2 A 3 y cosas así.

Paso 4. Ahora une el segmento de línea y el rayo, BA 13 .

Paso 5. Por lo tanto, el punto A 5 , construye una línea paralela a BA 13 que forma un ángulo igual a ∠AA 13 B.

Paso 6. El punto A 5 se cruza con la línea AB en el punto X.

Paso 7 X es el punto que divide al segmento AB en la razón de 5:8.

Paso 8. Así, mida las longitudes de la línea AX y XB. Por lo tanto, mide 2,9 cm y 4,7 cm respectivamente.

Class 10 NCERT Chapter 11 Exercise 11.1 Solution

Justificación:

La construcción puede justificarse demostrando que

\frac{AX}{XB} = \frac{5}{ 8}

De la construcción, tenemos A 5 X || A 13 B. Por el teorema básico de proporcionalidad para el triángulo AA 13 B, obtendremos

\frac{AX}{XB} =\frac{AA_5}{A_5A_{13}} ….. (1)

Por la figura que hemos construido, se puede ver que AA 5 y A 5 A 13 contienen 5 y 8 divisiones iguales de segmentos de línea respectivamente.

De este modo,

\frac{AA_5}{A_5A_{13}}=\frac{5}{8} … (2)

Comparando las ecuaciones (1) y (2), obtenemos

\frac{AX}{XB} = \frac{5}{ 8}

Por lo tanto, Justificado.

Pregunta 2. Construye un triángulo de lados 4 cm, 5 cm y 6 cm y luego un triángulo semejante cuyos lados sean 2/3 de los lados correspondientes del primer triángulo.

Solución:

Pasos de construcción:

Paso 1. Dibuja un segmento de recta XY que mida 4 cm, entonces XY = 4 cm.

Paso 2. Tomando el punto X como centro, y construya un arco de 5 cm de radio.

Paso 3. Del mismo modo, partiendo del punto Y como centro, traza un arco de 6 cm de radio.

Paso 4. Así, los siguientes arcos dibujados se intersecarán en el punto Z.

Paso 5. Ahora, tenemos XZ = 5 cm e YZ = 6 cm y, por lo tanto, ΔXYZ es el triángulo requerido.

Paso 6. Dibuja un rayo XA que forme un ángulo agudo a lo largo del segmento de línea XY en el lado opuesto del vértice Z.

Paso 7. Marque los 3 puntos como X 1 , X 2 , X 3 (ya que 3 es mayor entre 2 y 3) en la línea XA de modo que se convierta en XX 1 = X 1 X 2 = X 2 X 3 .

Paso 8. Une el punto YX 3 y construye una línea a través de X 2 que sea paralela a la línea YX 3 que interseca a XY en el punto Y’.

Paso 9. Desde el punto Y’, construya una línea paralela a la línea YZ que corte a la línea XZ en Z’.

Paso 10. Por lo tanto, ΔXY’Z’ es el triángulo requerido.

Class 10 NCERT Chapter 11 Exercise 11.1 Solution

Justificación:

La construcción puede justificarse demostrando que

XY' = \frac{2}{3}XY\\ Y'Z' = \frac{2}{3}YZ\\ XZ'= \frac{2}{3}XZ

De la construcción, obtenemos Y’Z’ || YZ

∴ ∠XY’Z’ = ∠XYZ (Ángulos correspondientes)

En ΔXY’Z’ y ΔXYZ,

∠XYZ = ∠XY’Z (Probado arriba)

∠YXZ = ∠Y’XZ’ (Común)

∴ ΔXY’Z’ ∼ ΔXYZ (Del criterio de similitud AA)

Por lo tanto, 

\frac{XY'}{XY} = \frac{Y'Z'}{YZ}= \frac{XZ'}{XZ}  …. (1)

En ΔXXY’ y ΔXXY,

∠X 2 XY’ =∠X 3 XY (Común)

De los ángulos correspondientes, obtenemos,

∠AA 2 B’ =∠AA 3 B

Por lo tanto, por el criterio de similitud AA, obtenemos

ΔXX 2 Y’ y XX 3 Y

Asi que, \frac{XY'}{XY} = \frac{XX_2}{XX_3}

Por lo tanto, \frac{XY'}{XY} = \frac{2}{3}  ……. (2)

De las ecuaciones (1) y (2), obtenemos

\frac{XY'}{XY}=\frac{Y'Z'}{YZ} = \frac{XZ'}{ XZ} = \frac{2}{3}

esta escrito como

XY’ = \frac{2}{3}XY

Y’Z’ = \frac{2}{3}YZ

XZ’=  \frac{2}{3}XZ

Por lo tanto, justificado.

Pregunta 3. Construye un triángulo con lados de 5 cm, 6 cm y 7 cm y luego otro triángulo cuyos lados sean 7/5 de los lados correspondientes del primer triángulo

Solución:

Pasos de construcción:

Paso 1. Construye un segmento de recta XY =5 cm.

Paso 2. Tomando X e Y como centro, y construya los arcos de radio 6 cm y 5 cm respectivamente.

Paso 3. Estos dos arcos se intersecarán en el punto Z y, por lo tanto, ΔXYZ es el triángulo requerido con una longitud de lados de 5 cm, 6 cm y 7 cm, respectivamente.

Paso 4. Construya un rayo XA que forme un ángulo agudo con el segmento de línea XY en el lado opuesto del vértice Z.

Paso 5. Señale los 7 puntos como X 1 , X 2 , X 3 , X 4 , X 5 , X 6 , X 7 (ya que 7 es mayor entre 5 y 7), en la línea XA tal que se convierte en XX 1 = X 1 X 2 = X 2 X 3 = X 3 X 4 = X 4 X 5 = X 5 X 6 = X 6 X 7

Paso 6. Una los puntos YX 5 y construya una línea de X 7 a YX 5 que sea paralela a la línea YX 5 donde se cruza con el segmento de línea extendido XY en el punto Y’.

Paso 7. Ahora, construya una línea desde Y’ el segmento de línea extendido XZ en Z’ que sea paralelo a la línea YZ, y se interseca para formar un triángulo.

Paso 8. Por lo tanto, ΔXY’Z’ es el triángulo necesario.

Class 10 NCERT Chapter 11 Exercise 11.1 Solution

Justificación:

La construcción puede justificarse demostrando que

XY’ = \frac{7}{5}XY

Y’Z’ = \frac{7}{5}YZ

XZ’= \frac{7}{5}XZ

Por la construcción, tenemos Y’Z’ || YZ

Por lo tanto,

∠XY’Z’ = ∠XYZ {Ángulos correspondientes}

En ΔXY’Z’ y ΔXYZ,

∠XYZ = ∠XY’Z {Como se muestra arriba}

∠YXZ = ∠Y’XZ’ {Común}

Por lo tanto,

ΔXY’Z’ ∼ ΔXYZ { Por criterio de similitud AA}

Por lo tanto, 

\frac{XY'}{XY} = \frac{Y'Z'}{YZ}= \frac{XZ'}{XZ}  …. (1)

En ΔXX 7 Y’ y ΔXX 5 Y,

∠X 7 XY’=∠X 5 XY (Común)

De los ángulos correspondientes, obtendremos,

∠XX 7 Y’=∠XX 5 Y

Por lo tanto, por el criterio de similitud AA, obtendremos

ΔXX 2 Y’ y XX 3 Y

De este modo, \frac{XY'}{XY} = \frac{XX_5}{XX_7}

Por lo tanto,  \frac{XY }{XY'} = \frac{5}{7}  ……. (2)

De las ecuaciones (1) y (2), obtenemos

\frac{XY'}{XY} = \frac{Y'Z'}{YZ} = \frac{XZ'}{ XZ} = \frac{7}{5}

También se puede mostrar como

XY’ = \frac{7}{5}XY

Y’Z’ =  \frac{7}{5}YZ

XZ’= \frac{7}{5}XZ

Por lo tanto, justificado.

Pregunta 4. Construye un triángulo isósceles cuya base sea 8 cm y una altura de 4 cm y luego otro triángulo cuyos lados sean 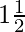 1\frac{1}{2} multiplicados por los lados correspondientes del triángulo isósceles

Solución:

Pasos de construcción:

Paso 1. Construye un segmento de línea YZ de 8 cm.

Paso 2. Ahora construya la bisectriz perpendicular del segmento de línea YZ e interseque en el punto A.

Paso 3. Tomando el punto A como centro y dibuja un arco con un radio de 4 cm que corte la mediatriz en el punto X.

Paso 4. Une las líneas XY y XZ y el triángulo es el triángulo requerido.

Paso 5. Construya un rayo YB que forme un ángulo agudo con la línea YZ en el lado opuesto al vértice X.

Paso 6. Marcar los 3 puntos Y 1 , Y 2 e Y 3 sobre la semirrecta YB tales que YY 1 = Y 1 Y 2 = Y 2 Y 3

Paso 7. Una los puntos Y 2 Z y construya una línea desde Y 3 que sea paralela a la línea Y 2 Z donde se cruza con el segmento de línea extendido YZ en el punto Z’.

Paso 8. Ahora, dibuja una línea desde Z’ el segmento de línea extendido XZ en X’, que es paralelo a la línea XZ, y se cruza para formar un triángulo.

Paso 9. Por lo tanto, ΔX’YZ’ es el triángulo requerido. 

Class 10 NCERT Chapter 11 Exercise 11.1 Solution

Justificación:

La construcción puede justificarse demostrando que

X´Y = \frac{3}{2}XY

YZ’ = \frac{3}{2}YZ

X’Z’= \frac{3}{2}XZ

Por la construcción, obtendremos X’Z’ || XZ

Por lo tanto, 

∠ X’Z’Y = ∠XZY {Ángulos correspondientes}

En ΔX’YZ’ y ΔXYZ,

∠Y = ∠Y (común)

∠X’YZ’ = ∠XZY

Por lo tanto,

ΔX’YZ’ ∼ ΔXYZ {Por criterio de similitud AA}

Por eso, 

\frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z}{XZ}

Por lo tanto, los lados correspondientes del triángulo similar están en la misma proporción, obtenemos

\frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z'}{XZ} = \frac{3}{2}

Por lo tanto, justificado.

Pregunta 5. Dibuja un triángulo ABC con lado BC = 6 cm, AB = 5 cm y ∠ABC = 60°. Luego construye un triángulo cuyos lados sean 3/4 de los lados correspondientes del triángulo ABC.

Solución:

Pasos de construcción:

Paso 1. Construya un ΔXYZ con lado base YZ = 6 cm, XY = 5 cm y ∠XYZ = 60°.

Paso 2. Construye un rayo YA que forme un ángulo agudo con YZ en el lado opuesto del vértice X.

Paso 3. Marca 4 puntos (ya que 4 es mayor en 3 y 4), como Y 1 , Y 2 , Y 3 , Y 4 , en el segmento de línea YA.

Paso 4. Una los puntos Y 4 Z y construya una línea a través de Y 3 , paralela a Y 4 Z que interseque el segmento de línea YZ en Z’.

Paso 5. Construya una línea a través de Z’ paralela a la línea XZ que interseca a la línea XY en X’.

Paso 6. Por lo tanto, ΔX’YZ’ es el triángulo requerido.

Class 10 NCERT Chapter 11 Exercise 11.1 Solution

Justificación:

La construcción puede justificarse demostrando que

Como aquí el factor de escala es  \frac{3}{4}  , 

tenemos que probar

X´Y = \frac{3}{4}XY

YZ’ = \frac{3}{4}YZ

X’Z’= \frac{3}{4}XZ

De la construcción obtendremos X’Z’ || XZ

En ΔX’YZ’ y ΔXYZ,

Por lo tanto,

∠X’Z’Y = ∠XZY {Ángulos correspondientes}

∠Y = ∠Y {común}

Por lo tanto,

ΔX’YZ’ ∼ ΔXYZ {Por criterio de similitud AA}

Por lo tanto, los lados correspondientes del triángulo similar están en la misma proporción, obtenemos

Por lo tanto,

\frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z'}{XZ}

Así, se convierte 

\frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z'}{XZ} = \frac{3}{4}

Por lo tanto, justificado.

Pregunta 6. Dibuja un triángulo ABC con lado BC = 7 cm, ∠ B = 45°, ∠ A = 105°. Luego, construye un triángulo cuyos lados sean 4/3 veces los lados correspondientes de ∆ ABC.

Solución:

Para encontrar ∠Z:

Dado:

∠Y = 45°, ∠X = 105°

∠X+∠Y +∠Z = 180° {La suma de todos los ángulos interiores de un triángulo es 180°}

105°+45°+∠Z = 180°

∠Z = 180° − 150°

∠Z = 30°

Entonces, de la propiedad del triángulo, obtenemos ∠Z = 30°

Pasos de construcción:

Paso 1. Construya un ΔXYZ con medidas laterales de base YZ = 7 cm, ∠Y = 45° y ∠Z = 30°.

Paso 2. Construya un rayo YA que forme un ángulo agudo con YZ en el lado opuesto del vértice X.

Paso 3. Marca 4 puntos (ya que 4 es mayor en 4 y 3), como Y 1 , Y 2 , Y 3 , Y 4 , en la semirrecta YA.

Paso 4. Une los puntos Y 3 Z.

Paso 5. Construya una línea a través de Y 4 paralela a Y 3 Z que interseque la línea extendida YZ en Z’.

Paso 6. A través de Z’, construya una línea paralela a la línea YZ que interseque el segmento de línea extendido en Z’.

Paso 7. Por lo tanto, ΔX’YZ’ es el triángulo requerido.

Class 10 NCERT Chapter 11 Exercise 11.1 Solution

Justificación:

La construcción puede justificarse demostrando que

Aquí el factor de escala es  \frac{4}{3}, tenemos que probar

X´Y = \frac{4}{3}XY

YZ’ = \frac{4}{3}YZ

X’Z’= \frac{4}{3}XZ

De la construcción, obtenemos X’Z’ || XZ

En ΔX’YZ’ y ΔXYZ,

Por lo tanto. 

∠X’Z’Y = ∠XZY {Ángulos correspondientes}

∠Y = ∠Y {común}

Por lo tanto, 

ΔX’YZ’ ∼ ΔXYZ {Por criterio de similitud AA}

Dado que los lados correspondientes del triángulo similar están en la misma proporción, se convierte en

Por lo tanto, 

\frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z'}{XZ}

Obtenemos,

\frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z'}{XZ} = \frac{4}{3}  

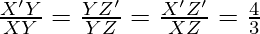
Por lo tanto, justificado.

Pregunta 7. Dibuja un triángulo rectángulo en el que los lados (aparte de la hipotenusa) miden 4 cm y 3 cm. Luego construye otro triángulo cuyos lados sean 5/3 veces los lados correspondientes del triángulo dado.

Solución:

Dado:

Los lados distintos de la hipotenusa miden 4 cm y 3 cm. Por lo tanto, los lados son perpendiculares entre sí.

Paso de construcción:

Paso 1. Construye un segmento de recta YZ =3 cm.

Paso 2. Ahora mide y dibuja ∠= 90°

Paso 3. Ahora tomando Y como centro y dibuja un arco con un radio de 4 cm y corta el rayo en el punto Y.

Paso 4. Une las líneas XZ y el triángulo XYZ es el triángulo requerido.

Paso 5. Construya un rayo YA que forme un ángulo agudo con YZ en el lado opuesto del vértice X.

Paso 6. Marque 5 como Y 1 , Y 2 , Y 3 , Y 4 , en el rayo YA tal que YY 1 = Y 1 Y 2 = Y 2 Y 3 = Y 3 Y 4 = Y 4 Y 5

Paso 7. Une los puntos Y 3 Z.

Paso 8. Construya una línea a través de Y 5 paralela a Y 3 Z que interseque la línea extendida YZ en Z’.

Paso 9. A través de Z’, dibuje una línea paralela a la línea XZ que interseque la línea extendida XY en X’.

Paso 10. Por lo tanto, ΔX’YZ’ es el triángulo requerido.

Class 10 NCERT Chapter 11 Exercise 11.1 Solution

Justificación:

La construcción puede justificarse demostrando que

Aquí el factor de escala es  \frac{5}{3}, necesitamos probar

X´Y = \frac{5}{3}XY

YZ’ = \frac{5}{3}YZ

X’Z’= \frac{5}{3}XZ

De la construcción, obtenemos X’Z’ || XZ

En ΔX’YZ’ y ΔXYZ,

Por lo tanto, 

∠X’Z’Y = ∠XZY {Ángulos correspondientes}

∠Y = ∠Y {común}

Por lo tanto, 

ΔX’YZ’ ∼ ΔXYZ {Por criterio de similitud AA}

Dado que los lados correspondientes del triángulo similar están en la misma proporción, se convierte en

Por lo tanto, 

\frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z'}{XZ}

Entonces, se convierte \frac{X'Y}{XY} = \frac{YZ'}{YZ}= \frac{X'Z'}{XZ} = \frac{5}{3}

Por lo tanto, justificado.

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *