Dado un grafo y un vértice de origen src en un grafo no dirigido ponderado , encuentre las rutas más cortas desde src a todos los vértices en el grafo dado. El gráfico puede contener bordes de peso negativos.
Para este problema, ya hemos discutido el algoritmo de Dijkstra y el algoritmo de Bellman -Ford . Pero el algoritmo D’Esopo-Pape funciona bastante bien en la mayoría de los casos. Sin embargo, hay algunos casos en los que lleva un tiempo exponencial.
Algoritmo:
Entrada: Lista de adyacencia del gráfico y origen del vértice de origen.
Salida: distancia más corta a todos los vértices desde src.
Este algoritmo utiliza una cola bidireccional que almacena los vértices a operar.
Los siguientes son los pasos detallados del algoritmo.
- Inicialice la distancia de los vértices desde la fuente hasta el infinito en una array.
- Mantenga una cola que almacenará los vértices que se operarán y también mantendrá una array booleana para los vértices que se usará para decidir si el vértice ya está presente en la cola o no.
- Agregue el vértice de origen en la cola.
- Comience a extraer vértices de la cola hasta que la cola esté vacía y realice los siguientes pasos para cada vértice extraído (sea U el vértice extraído):
- Establezca el vértice U como no presente en la cola.
- Para cada vértice adyacente V de U , verifique si su distancia mínima actual [V] es mayor que la distancia a través de U ,
es decir , Distancia [U] + peso del borde que conecta U y V . - En caso afirmativo, actualice Distancia[V] = Distancia[U] + peso del borde que conecta U y V.
Compruebe si V no está presente en la cola con la ayuda de la array booleana:- Si V ingresa a la cola por primera vez, agregue V al final de la cola y establezca el vértice V como presente en la cola con la ayuda de Boolean Array.
- De lo contrario, agregue al frente de la cola y establezca el vértice V como presente en la cola.
- Lista de retorno Distancia que tendrá la distancia más corta de cada vértice desde el vértice de origen.
Por Ejemplo:
Inicialmente, la Distancia de la fuente a sí misma será 0 y para otros vértices será infinita.
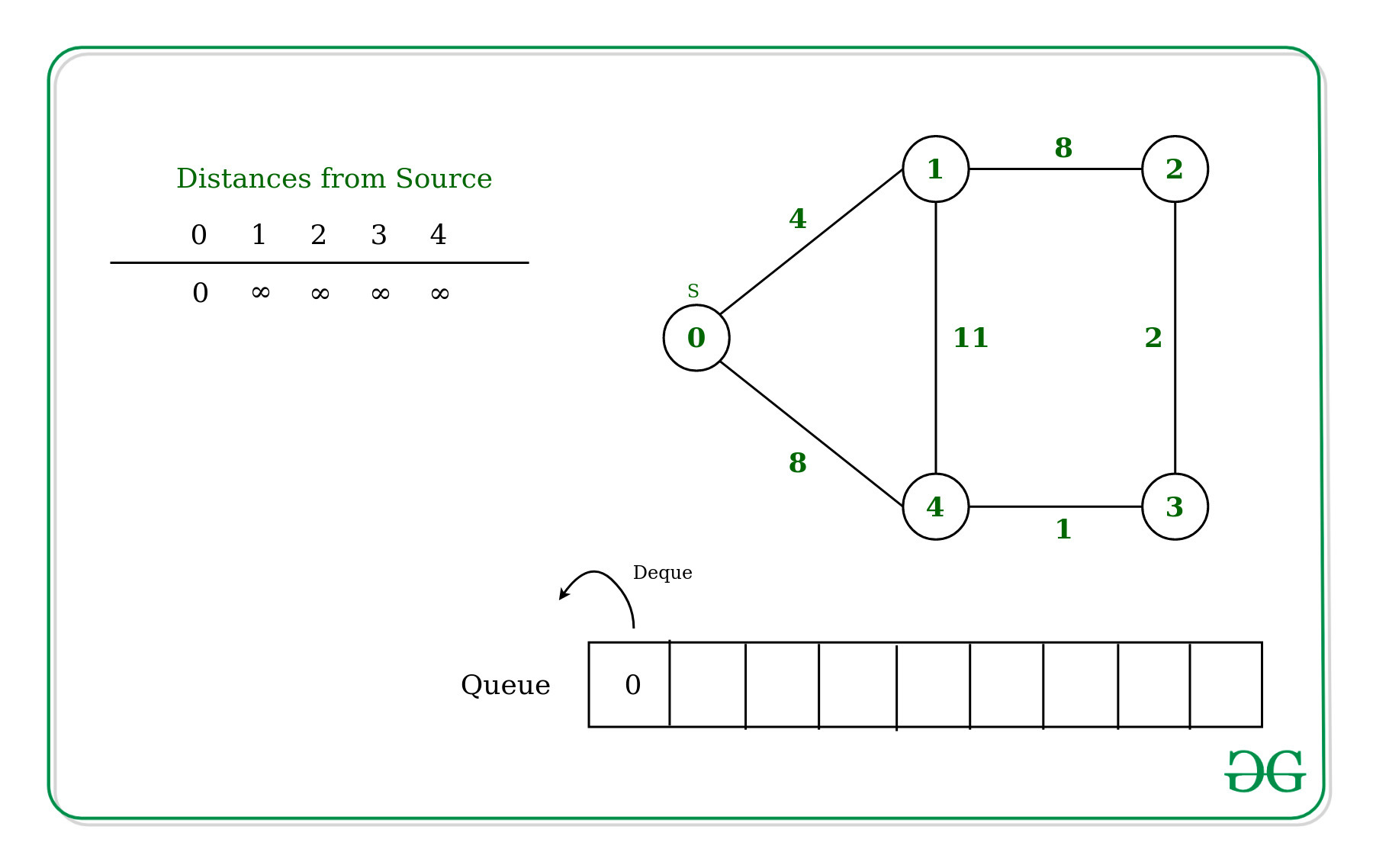
Ahora, para cada vértice adyacente de la fuente que es 0 en este caso, [1, 4] actualiza la distancia y marca los vértices como presentes en el con un peso de 4 y 8 respectivamente.

Ahora elimine la cola del vértice 4 de la cola y, a continuación, los vértices adyacentes están conectados al vértice 4:
- Vértice 1 : como el vértice 1 ya ha visitado y el peso para alcanzar el vértice 1 es 4, mientras que cuando se mueve al vértice 1 a través del borde 4 — 1 desde la fuente, el peso total será 11, que es mayor que el peso almacenado en la array de distancia .
- Vértice 3 : como el vértice 3 no se visita y tampoco está presente en la cola, la distancia se actualiza a 9 para el vértice 3 y también se coloca en la cola al frente.

De manera similar, elimine la cola del vértice 3 de la cola y actualice los valores para el vértice adyacente. Los vértices adyacentes del vértice 3 son el vértice 4 y el vértice 2.
- Vértice 4 : como el vértice 4 ya se visitó y el peso ya es mínimo, la distancia no se actualiza.
- Vértice 2 : como el vértice 2 no se visita y tampoco está presente en la cola, la distancia se actualiza a 11 para el vértice 3 y también se coloca en la cola al frente.

A continuación se muestra la implementación del enfoque anterior.
C++
// C++ implementation for
// D'Esopo-Pape algorithm
#include <bits/stdc++.h>
using namespace std;
#define inf INT_MAX
vector<int> desopo(vector<vector<int>> &graph)
{
// Number of vertices in graph
int v = graph.size();
// Adjacency list of graph
map<int, vector<pair<int, int>>> adj;
for(int i = 0; i < v; i++) {
for(int j = i + 1; j < v; j++)
{
if (graph[i][j] != 0)
{
adj[i].push_back({graph[i][j], j});
adj[j].push_back({graph[i][j], i});
}
}
}
// Queue to store unoperated vertices
deque<int> q;
// Distance from source vertex
// distance =[float('inf')]*v
vector<int> distance(v, inf);
// Status of vertex
vector<bool> is_in_queue(v, false);
// let 0 be the source vertex
int source = 0;
distance = 0;
q.push_back(source);
is_in_queue = true;
while (!q.empty())
{
// Pop from front of the queue
int u = q.front();
q.pop_front();
is_in_queue[u] = false;
// Scan adjacent vertices of u
for(auto e : adj[u])
{
// e <- [weight, vertex]
if (distance[e.second] >
distance[u] + e.first)
{
distance[e.second] = distance[u] + e.first;
if (!is_in_queue[e.second])
{
// if e.second is entering
// first time in the queue
if (distance[e.second] == inf)
// Append at back of queue
q.push_back(e.second);
else
// Append at front of queue
q.push_front(e.second);
is_in_queue[e.second] = true;
}
}
}
}
return distance;
}
// Driver Code
int main(int argc, char const *argv[])
{
// Adjacency matrix of graph
vector<vector<int>> graph = { { 0, 4, 0, 0, 8 },
{ 0, 0, 8, 0, 11 },
{ 0, 8, 0, 2, 0 },
{ 0, 0, 2, 0, 1 },
{ 8, 11, 0, 1, 0 } };
for(auto i : desopo(graph))
{
cout << i << " ";
}
return 0;
}
// This code is contributed by sanjeev2552
Python3
# Python3 implementation for
# D'Esopo-Pape algorithm
from collections import defaultdict, deque
def desopo(graph):
# Number of vertices in graph
v = len(graph)
# Adjacency list of graph
adj = defaultdict(list)
for i in range(v):
for j in range(i + 1, v):
if graph[i][j] != 0:
adj[i].append(
[graph[i][j], j]
)
adj[j].append(
[graph[i][j], i]
)
# Queue to store unoperated vertices
q = deque([])
# Distance from source vertex
distance =[float('inf')]*v
# Status of vertex
is_in_queue =[False]*v
# let 0 be the source vertex
source = 0
distance= 0
q.append(source)
is_in_queue= True
while q:
# Pop from front of the queue
u = q.popleft()
is_in_queue[u]= False
# scan adjacent vertices of u
for e in adj[u]:
# e <- [weight, vertex]
if distance[e[1]] > distance[u]+e[0]:
distance[e[1]]= distance[u]+e[0]
if is_in_queue[e[1]]== False:
# if e[1] is entering
# first time in the queue
if distance[e[1]]== float('inf'):
# Append at back of queue
q.append(e[1])
else:
# Append at front of queue
q.appendleft(e[1])
is_in_queue[e[1]] = True
return distance
# Driver Code
if __name__ == "__main__":
# Adjacency matrix of graph
graph = [[0, 4, 0, 0, 8],
[0, 0, 8, 0, 11],
[0, 8, 0, 2, 0],
[0, 0, 2, 0, 1],
[8, 11, 0, 1, 0]
]
print(desopo(graph))
[0, 4, 11, 9, 8]