Dados tres enteros m, n y k que almacenan el número de puntos en las líneas l1, l2 y l3 respectivamente que no se intersecan. La tarea es encontrar el número de triángulos que posiblemente se pueden formar a partir de este conjunto de puntos.
Ejemplos:
Input: m = 3, n = 4, k = 5 Output: 205
Input: m = 2, n = 2, k = 1 Output: 10
Acercarse:
- El número total de puntos son (m + n + k) que debe dar
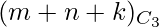 número de triángulos.
número de triángulos. - Pero ‘m’ apunta sobre ‘l1’ da
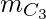 combinaciones que no pueden formar un triángulo.
combinaciones que no pueden formar un triángulo. - Del mismo modo, no
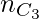 se
se 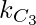 puede formar un número de triángulos.
puede formar un número de triángulos. - Por lo tanto, Número requerido de triángulos =
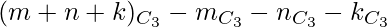
A continuación se muestra la implementación del enfoque anterior:
C++
// CPP program to find the possible number
// of triangles that can be formed from
// set of points on three lines
#include <bits/stdc++.h>
using namespace std;
// Returns factorial of a number
int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// calculate c(n, r)
int ncr(int n, int r)
{
return factorial(n) / (factorial(r) * factorial(n - r));
}
// Driver code
int main()
{
int m = 3, n = 4, k = 5;
int totalTriangles = ncr(m + n + k, 3) - ncr(m, 3)
- ncr(n, 3) - ncr(k, 3);
cout << totalTriangles << endl;
}
Java
// Java program to find the possible number
// of triangles that can be formed from
// set of points on three lines
import java.io.*;
class GFG {
// Returns factorial of a number
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// calculate c(n, r)
static int ncr(int n, int r)
{
return factorial(n)
/ (factorial(r) * factorial(n - r));
}
// Driver code
public static void main(String[] args)
{
int m = 3, n = 4, k = 5;
int totalTriangles = ncr(m + n + k, 3) - ncr(m, 3)
- ncr(n, 3) - ncr(k, 3);
System.out.println(totalTriangles);
}
}
Python 3
# Python 3 program to find the # possible number of triangles # that can be formed from set of # points on three lines # Returns factorial of a number def factorial(n): fact = 1 for i in range(2, n + 1): fact = fact * i return fact # calculate c(n, r) def ncr(n, r): return (factorial(n) // (factorial(r) * factorial(n - r))) # Driver code if __name__ == "__main__": m = 3 n = 4 k = 5 totalTriangles = (ncr(m + n + k, 3) - ncr(m, 3) - ncr(n, 3) - ncr(k, 3)) print(totalTriangles) # This code is contributed # by ChitraNayal
C#
// C# program to find the possible number
// of triangles that can be formed from
// set of points on three lines
using System;
class GFG
{
// Returns factorial of a number
static int factorial(int n)
{
int fact = 1;
for (int i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// calculate c(n, r)
static int ncr(int n, int r)
{
return factorial(n) / (factorial(r) *
factorial(n - r));
}
// Driver code
public static void Main ()
{
int m = 3, n = 4, k = 5;
int totalTriangles = ncr(m + n + k, 3) -
ncr(m, 3) - ncr(n, 3) -
ncr(k, 3);
Console.WriteLine (totalTriangles);
}
}
// This code is contributed
// by anuj_67..
PHP
<?php
// PHP program to find the possible
// number of triangles that can be
// formed from set of points on
// three lines
// Returns factorial of a number
function factorial($n)
{
$fact = 1;
for ($i = 2; $i <= $n; $i++)
$fact = $fact * $i;
return $fact;
}
// calculate c(n, r)
function ncr($n, $r)
{
return factorial($n) / (factorial($r) *
factorial($n - $r));
}
// Driver code
$m = 3; $n = 4; $k = 5;
$totalTriangles = ncr($m + $n + $k, 3) -
ncr($m, 3) - ncr($n, 3) -
ncr($k, 3);
echo $totalTriangles . "\n";
// This code is contributed
// by Akanksha Rai
Javascript
<script>
//JavaScript program to find the possible number
// of triangles that can be formed from
// set of points on three lines
// Returns factorial of a number
function factorial(n)
{
var fact = 1;
for (i = 2; i <= n; i++)
fact = fact * i;
return fact;
}
// calculate c(n, r)
function ncr(n , r)
{
return factorial(n)
/ (factorial(r) * factorial(n - r));
}
// Driver code
var m = 3, n = 4, k = 5;
var totalTriangles = ncr(m + n + k, 3) -
ncr(m, 3) - ncr(n, 3) - ncr(k, 3);
document.write(totalTriangles);
// This code is contributed by 29AjayKumar
</script>
Producción:
205
Complejidad temporal: O(m + n + k)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por SURENDRA_GANGWAR y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA