Dada una array triángulos[][] que consta de N triángulos de la forma {x1, y1, x2, y2, x3, y3} y una array cortes[] que consta de M líneas horizontales y verticales de la forma “X=x” o “Y=y” que representa la ecuación de los segmentos de recta. La tarea es imprimir el número de triángulos intersecados por cada corte de tal manera que las partes izquierda y derecha del triángulo tengan áreas mayores que cero.
Ejemplos:
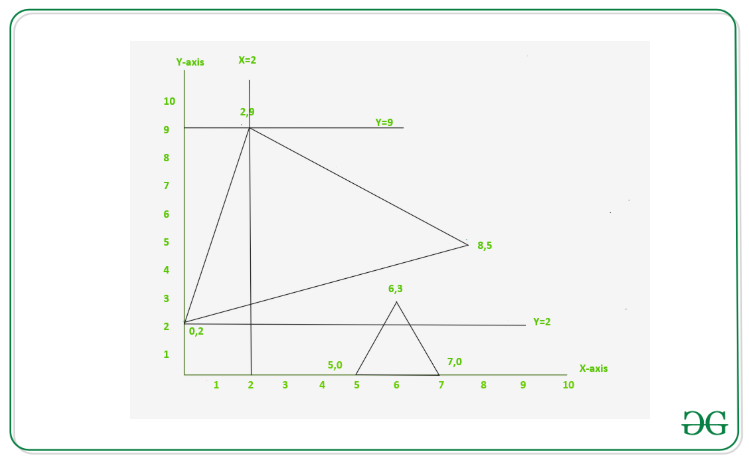
Entrada: N = 2, triángulos[][] = {{0, 2, 2, 9, 8, 5}, {5, 0, 6, 3, 7, 0}}, M = 3, cortes[] = {“X=2”, “Y=2”, “Y=9”}
Salida: 1 1 0
Explicación:
El corte en X = 2 divide el primer triángulo que tiene vértices (0, 2), (2, 9) y (8, 5)
El corte en Y = 2 divide el segundo triángulo que tiene vértices (5, 0), (6, 3) y (7, 0)
El corte en Y = 9 no divide ninguno de los triángulos.Entrada: N = 2, triángulos[][] = {{0, 2, 2, 9, 8, 5}}, M = 3, cortes[] = {“X=7”, “Y=7”, “ X=9”}
Salida: 1 1 0
Explicación:
El corte en X = 2 divide el primer triángulo que tiene vértices (0, 2), (2, 9) y (8, 5)
El corte en Y = 2 divide el segundo triángulo que tiene vértices (5, 0), (6, 3) y (7, 0)
El corte en Y = 9 no divide ninguno de los triángulos.
Enfoque: a continuación se muestran las condiciones para que un segmento de línea divida un triángulo en dos partes que tienen áreas distintas de cero:
- Si se hace un corte en el eje X y se encuentra estrictamente entre la coordenada X mínima y máxima de un triángulo, entonces divide el triángulo de tal manera que las partes izquierda y derecha deben tener áreas mayores que cero.
- De manera similar, si se hace un corte en el eje Y y se encuentra estrictamente entre la coordenada Y mínima y máxima de un triángulo, entonces divide el triángulo de tal manera que las partes izquierda y derecha deben tener áreas mayores que cero. .
Siga los pasos a continuación para resolver el problema:
- Cree una estructura para almacenar las coordenadas X e Y máximas y mínimas para cada triángulo.
- Atraviese la array cuts[] array sobre el rango [0, M – 1] .
- Para cada corte, inicialice un recuento de contadores con 0 para almacenar la respuesta del corte actual y comience a recorrer la array de triángulos [] desde j = 0 hasta N – 1 .
- Verifique para cada triángulo, cortes[i] tiene la forma X=x , es decir, corte vertical y x se encuentra estrictamente entre la coordenada X máxima y mínima del i -ésimo triángulo, incremente el conteo del contador; de lo contrario, continúe verificando otros triángulos para cada corte .
- Después de calcular la respuesta para cortes[i] , imprima el conteo .
- Repita los pasos anteriores para cada corte e imprima el conteo de triángulos cortados por cada línea.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Store the minimum and maximum
// X and Y coordinates
struct Tri {
int MinX, MaxX, MinY, MaxY;
};
// Function to convert string to int
int StringtoInt(string s)
{
stringstream geek(s);
int x;
geek >> x;
return x;
}
// Function to print the number of
// triangles cut by each line segment
int TriangleCuts(
vector<vector<int> > Triangle,
string Cuts[], int N, int M, int COL)
{
// Initialize Structure
Tri Minimized[N];
// Find maximum and minimum X and Y
// coordinates for each triangle
for (int i = 0; i < N; i++) {
int x1 = Triangle[i][0];
int y1 = Triangle[i][1];
int x2 = Triangle[i][2];
int y2 = Triangle[i][3];
int x3 = Triangle[i][4];
int y3 = Triangle[i][5];
// Minimum X
Minimized[i].MinX
= min({ x1, x2, x3 });
// Maximum X
Minimized[i].MaxX
= max({ x1, x2, x3 });
// Minimum Y
Minimized[i].MinY
= min({ y1, y2, y3 });
// Maximum Y
Minimized[i].MaxY
= max({ y1, y2, y3 });
}
// Traverse each cut from 0 to M-1
for (int i = 0; i < M; i++) {
string Cut = Cuts[i];
// Store number of triangles cut
int CutCount = 0;
// Extract value from the line
// segment string
int CutVal = StringtoInt(
Cut.substr(2, Cut.size()));
// If cut is made on X-axis
if (Cut[0] == 'X') {
// Check for each triangle
// if x lies b/w max and
// min X coordinates
for (int j = 0; j < N; j++) {
if ((Minimized[j].MinX)
< (CutVal)
&& (Minimized[j].MaxX)
> (CutVal)) {
CutCount++;
}
}
}
// If cut is made on Y-axis
else if (Cut[0] == 'Y') {
// Check for each triangle
// if y lies b/w max and
// min Y coordinates
for (int j = 0; j < N; j++) {
if ((Minimized[j].MinY)
< (CutVal)
&& (Minimized[j].MaxY)
> (CutVal)) {
CutCount++;
}
}
}
// Print answer for ith cut
cout << CutCount << " ";
}
}
// Driver Code
int main()
{
// Given coordinates of triangles
vector<vector<int> > Triangle
= { { 0, 2, 2, 9, 8, 5 },
{ 5, 0, 6, 3, 7, 0 } };
int N = Triangle.size();
int COL = 6;
// Given cuts of lines
string Cuts[] = { "X=2", "Y=2", "Y=9" };
int M = sizeof(Cuts) / sizeof(Cuts[0]);
// Function Call
TriangleCuts(Triangle, Cuts,
N, M, COL);
return 0;
}
Java
// Java program for the above approach
import java.util.*;
class GFG{
// Store the minimum and maximum
// X and Y coordinates
static class Tri
{
int MinX, MaxX, MinY, MaxY;
};
// Function to convert String to int
static int StringtoInt(String s)
{
return Integer.valueOf(s);
}
static int min(int a, int b, int c)
{
return Math.min(a, Math.min(b, c));
}
static int max(int a, int b, int c)
{
return Math.max(a, Math.max(b, c));
}
// Function to print the number of
// triangles cut by each line segment
static void TriangleCuts(int[][] Triangle,
String Cuts[], int N, int M, int COL)
{
// Initialize Structure
Tri []Minimized = new Tri[N];
for(int i = 0; i < N; i++)
{
Minimized[i] = new Tri();
Minimized[i].MaxX = 0;
Minimized[i].MaxY = 0;
Minimized[i].MinX = 0;
Minimized[i].MinY = 0;
}
// Find maximum and minimum X and Y
// coordinates for each triangle
for(int i = 0; i < N; i++)
{
int x1 = Triangle[i][0];
int y1 = Triangle[i][1];
int x2 = Triangle[i][2];
int y2 = Triangle[i][3];
int x3 = Triangle[i][4];
int y3 = Triangle[i][5];
// Minimum X
Minimized[i].MinX = min(x1, x2, x3);
// Maximum X
Minimized[i].MaxX = max(x1, x2, x3);
// Minimum Y
Minimized[i].MinY = min(y1, y2, y3);
// Maximum Y
Minimized[i].MaxY = max(y1, y2, y3);
}
// Traverse each cut from 0 to M-1
for(int i = 0; i < M; i++)
{
String Cut = Cuts[i];
// Store number of triangles cut
int CutCount = 0;
// Extract value from the line
// segment String
int CutVal = StringtoInt(
Cut.substring(2, Cut.length()));
// If cut is made on X-axis
if (Cut.charAt(0) == 'X')
{
// Check for each triangle
// if x lies b/w max and
// min X coordinates
for(int j = 0; j < N; j++)
{
if ((Minimized[j].MinX) < (CutVal) &&
(Minimized[j].MaxX) > (CutVal))
{
CutCount++;
}
}
}
// If cut is made on Y-axis
else if (Cut.charAt(0) == 'Y')
{
// Check for each triangle
// if y lies b/w max and
// min Y coordinates
for(int j = 0; j < N; j++)
{
if ((Minimized[j].MinY) < (CutVal) &&
(Minimized[j].MaxY) > (CutVal))
{
CutCount++;
}
}
}
// Print answer for ith cut
System.out.print(CutCount + " ");
}
}
// Driver Code
public static void main(String[] args)
{
// Given coordinates of triangles
int[][] Triangle = { { 0, 2, 2, 9, 8, 5 },
{ 5, 0, 6, 3, 7, 0 } };
int N = Triangle.length;
int COL = 6;
// Given cuts of lines
String Cuts[] = { "X=2", "Y=2", "Y=9" };
int M = Cuts.length;
// Function Call
TriangleCuts(Triangle, Cuts,
N, M, COL);
}
}
// This code is contributed by Princi Singh
Python3
# Python program for the above approach # Store the minimum and maximum # X and Y coordinates class Tri: def __init__(self, MinX, MaxX, MinY, MaxY): self.MinX = MinX self.MaxX = MaxX self.MinY = MinY self.MaxY = MaxY # Function to convert string to int def StringtoInt(s): x = int(s) return x # Function to print the number of # triangles cut by each line segment def TriangleCuts(Triangle, Cuts, N, M, COL): # Initialize Structure Minimized = [] # Find maximum and minimum X and Y # coordinates for each triangle for i in range(N): x1 = Triangle[i][0] y1 = Triangle[i][1] x2 = Triangle[i][2] y2 = Triangle[i][3] x3 = Triangle[i][4] y3 = Triangle[i][5] # Minimum X MinX = min(x1, x2, x3) # Maximum X MaxX = max(x1, x2, x3) # Minimum Y MinY = min(y1, y2, y3) # Maximum Y MaxY = max(y1, y2, y3) Minimized.append(Tri(MinX, MaxX, MinY, MaxY)) # Traverse each cut from 0 to M-1 for i in range(M): Cut = Cuts[i] # Store number of triangles cut CutCount = 0 # Extract value from the line # segment string CutVal = StringtoInt(Cut[2:len(Cut)]) # If cut is made on X-axis if Cut[0] == 'X': # Check for each triangle # if x lies b/w max and # min X coordinates for j in range(N): if (Minimized[j].MinX) < (CutVal) and (Minimized[j].MaxX) > (CutVal): CutCount = CutCount + 1 # If cut is made on Y-axis elif Cut[0] == 'Y': # Check for each triangle # if y lies b/w max and # min Y coordinates for j in range(N): if (Minimized[j].MinY) < (CutVal) and (Minimized[j].MaxY) > (CutVal): CutCount = CutCount + 1 # Print answer for ith cut print(CutCount, end=' ') # Driver Code if __name__ == "__main__": # Given coordinates of triangles Triangle = [[0, 2, 2, 9, 8, 5], [5, 0, 6, 3, 7, 0]] N = len(Triangle) COL = 6 # Given cuts of lines Cuts = ["X=2", "Y=2", "Y=9"] M = len(Cuts) # Function Call TriangleCuts(Triangle, Cuts, N, M, COL) # The code is contributed by Gautam goel (gautamgoel962)
C#
// C# program for the above approach
using System;
class GFG{
// Store the minimum and maximum
// X and Y coordinates
public class Tri
{
public int MinX, MaxX, MinY, MaxY;
};
// Function to convert String to int
static int StringtoInt(String s)
{
return Int32.Parse(s);
}
static int min(int a, int b, int c)
{
return Math.Min(a, Math.Min(b, c));
}
static int max(int a, int b, int c)
{
return Math.Max(a, Math.Max(b, c));
}
// Function to print the number of
// triangles cut by each line segment
static void TriangleCuts(int[,] Triangle,
String []Cuts,
int N, int M,
int COL)
{
// Initialize Structure
Tri []Minimized = new Tri[N];
for(int i = 0; i < N; i++)
{
Minimized[i] = new Tri();
Minimized[i].MaxX = 0;
Minimized[i].MaxY = 0;
Minimized[i].MinX = 0;
Minimized[i].MinY = 0;
}
// Find maximum and minimum X and Y
// coordinates for each triangle
for(int i = 0; i < N; i++)
{
int x1 = Triangle[i, 0];
int y1 = Triangle[i, 1];
int x2 = Triangle[i, 2];
int y2 = Triangle[i, 3];
int x3 = Triangle[i, 4];
int y3 = Triangle[i, 5];
// Minimum X
Minimized[i].MinX = min(x1, x2, x3);
// Maximum X
Minimized[i].MaxX = max(x1, x2, x3);
// Minimum Y
Minimized[i].MinY = min(y1, y2, y3);
// Maximum Y
Minimized[i].MaxY = max(y1, y2, y3);
}
// Traverse each cut from 0 to M-1
for(int i = 0; i < M; i++)
{
String Cut = Cuts[i];
// Store number of triangles cut
int CutCount = 0;
// Extract value from the line
// segment String
int CutVal = StringtoInt(
Cut.Substring(2, Cut.Length - 2));
// If cut is made on X-axis
if (Cut[0] == 'X')
{
// Check for each triangle
// if x lies b/w max and
// min X coordinates
for(int j = 0; j < N; j++)
{
if ((Minimized[j].MinX) < (CutVal) &&
(Minimized[j].MaxX) > (CutVal))
{
CutCount++;
}
}
}
// If cut is made on Y-axis
else if (Cut[0] == 'Y')
{
// Check for each triangle
// if y lies b/w max and
// min Y coordinates
for(int j = 0; j < N; j++)
{
if ((Minimized[j].MinY) < (CutVal) &&
(Minimized[j].MaxY) > (CutVal))
{
CutCount++;
}
}
}
// Print answer for ith cut
Console.Write(CutCount + " ");
}
}
// Driver Code
public static void Main(String[] args)
{
// Given coordinates of triangles
int[,] Triangle = { { 0, 2, 2, 9, 8, 5 },
{ 5, 0, 6, 3, 7, 0 } };
int N = Triangle.GetLength(0);
int COL = 6;
// Given cuts of lines
String []Cuts = { "X=2", "Y=2", "Y=9" };
int M = Cuts.Length;
// Function Call
TriangleCuts(Triangle, Cuts,
N, M, COL);
}
}
// This code is contributed by Princi Singh
1 1 0
Complejidad temporal: O(M*N)
Espacio auxiliar: O(M+N)
Publicación traducida automáticamente
Artículo escrito por satvikshrivas26 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA