Dado un número entero N . La tarea es encontrar la suma de N términos de la serie dada:
2×3 + 4×4 + 6×5 + 8×6 + … + hasta n términos
Ejemplos:
Input : N = 5 Output : Sum = 170 Input : N = 10 Output : Sum = 990
Sea t N el término N-ésimo de la serie . t 1 = 2 × 3 = (2 × 1)(1 + 2) t 2 = 4 × 4 = (2 × 2)(2 + 2) t 3 = 6 × 5 = (2 × 3)(3 + 2 ) t 4 = 8 × 6 = (2 × 4)(4 + 2) . . . t N = (2 × N)(N + 2) La suma de n términos de la serie,
Sn = t1 + t2 +... + tn
=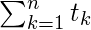 =
=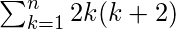 =
=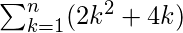 =
=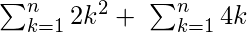 =
=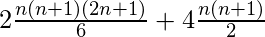 =
=![Rendered by QuickLaTeX.com n(n+1)[ \frac{2n+1}{3} +2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-99c6f9cfaab5d8ed8fc1d09d69e72104_l3.png) =
=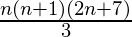
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program to find sum upto
// N term of the series:
// 2 × 3 + 4 × 4 + 6 × 5 + 8 × 6 + ...
#include<iostream>
using namespace std;
// calculate sum upto N term of series
void Sum_upto_nth_Term(int n)
{
int r = n * (n + 1) *
(2 * n + 7) / 3;
cout << r;
}
// Driver code
int main()
{
int N = 5;
Sum_upto_nth_Term(N) ;
return 0;
}
Java
// Java program to find sum upto
// N term of the series:
import java.io.*;
class GFG {
// calculate sum upto N term of series
static void Sum_upto_nth_Term(int n)
{
int r = n * (n + 1) *
(2 * n + 7) / 3;
System.out.println(r);
}
// Driver code
public static void main (String[] args) {
int N = 5;
Sum_upto_nth_Term(N);
}
}
Python3
# Python program to find sum upto N term of the series: # 2 × 3 + 4 × 4 + 6 × 5 + 8 × 6 + ... # calculate sum upto N term of series def Sum_upto_nth_Term(n): return n * (n + 1) * (2 * n + 7) // 3 # Driver code N = 5 print(Sum_upto_nth_Term(N))
C#
// C# program to find sum upto
// N term of the series:
// 2 × 3 + 4 × 4 + 6 × 5 + 8 × 6 + ...
using System;
class GFG
{
// calculate sum upto N term of series
static void Sum_upto_nth_Term(int n)
{
int r = n * (n + 1) *
(2 * n + 7) / 3;
Console.Write(r);
}
// Driver code
public static void Main()
{
int N = 5;
Sum_upto_nth_Term(N);
}
}
// This code is contributed
// by Akanksha Rai(Abby_akku)
PHP
<?php
// PHP program to find sum upto
// N term of the series:
// 2 × 3 + 4 × 4 + 6 × 5 + 8 × 6 + ...
function Sum_upto_nth_Term($n)
{
$r = $n * ($n + 1) *
(2 * $n + 7) / 3;
echo $r;
}
// Driver code
$N = 5;
Sum_upto_nth_Term($N);
// This code is contributed
// by Shashank_Sharma
?>
Javascript
<script>
// Javascript program to find sum upto
// N term of the series:
// 2 × 3 + 4 × 4 + 6 × 5 + 8 × 6 + ...
// calculate sum upto N term of series
function Sum_upto_nth_Term(n)
{
let r = n * (n + 1) *
(2 * n + 7) / 3;
document.write(r);
}
// Driver code
let N = 5;
Sum_upto_nth_Term(N) ;
// This code is contributed by Mayank Tyagi
</script>
Producción:
170
Complejidad Temporal: O(1), es una constante.
Espacio Auxiliar: O(1), no se requiere espacio extra.
Publicación traducida automáticamente
Artículo escrito por Sanjit_Prasad y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA