Área del Circuncírculo de un Triángulo Equilátero usando la Mediana

Dada la mediana del triángulo equilátero M , la tarea es encontrar el área del círculo circunscrito de este triángulo equilátero usando la mediana M.
Ejemplos: 
 

Entrada: M = 3 
Salida: 12,5664
Entrada: M = 6 
Salida: 50,2655 
 

Enfoque: La observación clave en el problema es que el baricentro, el circuncentro, el ortocentro y el incentro de un triángulo equilátero se encuentran todos en el mismo punto. 
 

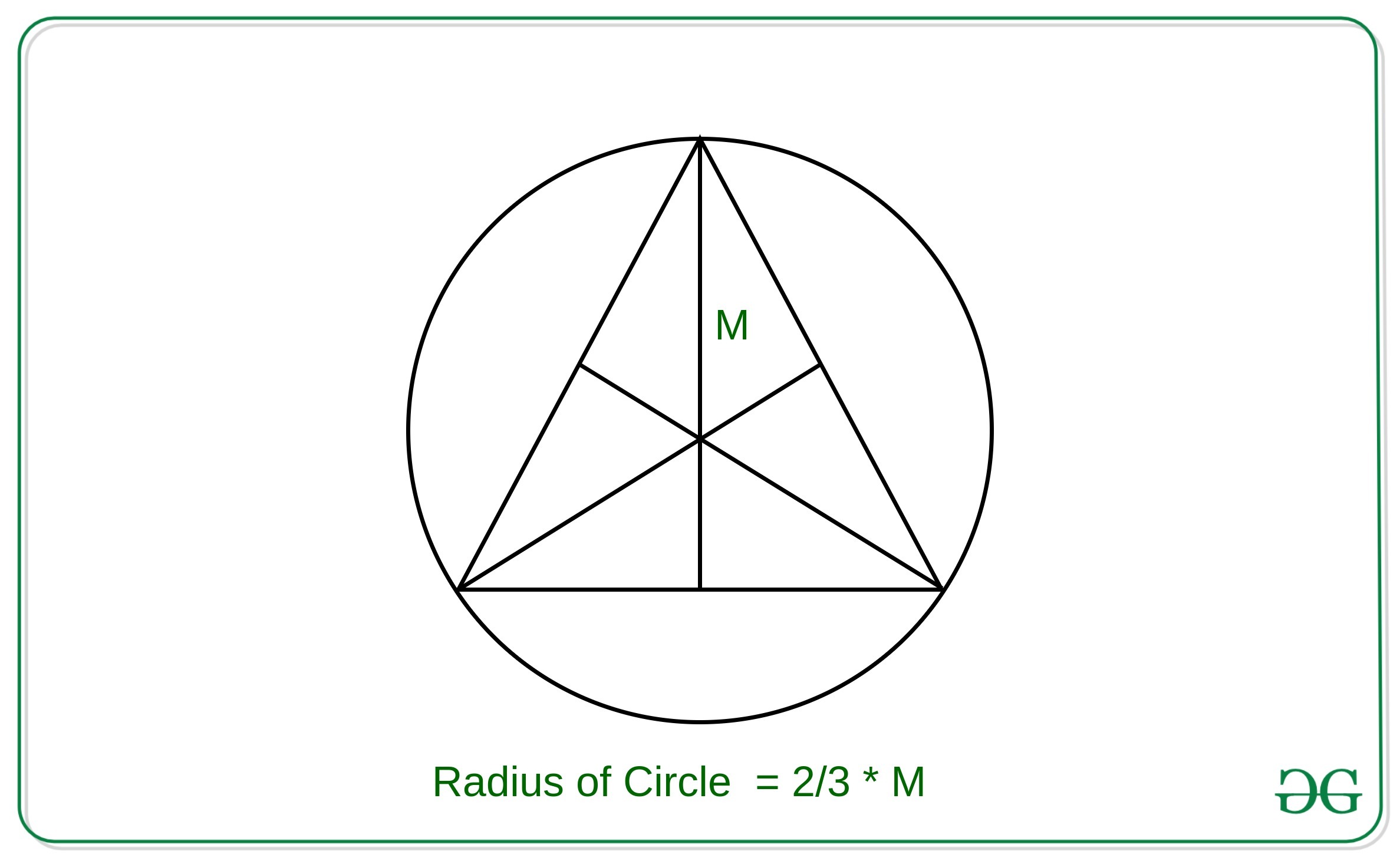
Por lo tanto, el radio del círculo con la mediana dada del triángulo equilátero inscrito en el círculo se puede derivar como: 

Luego, el área del círculo se puede calcular utilizando el enfoque utilizado en este artículo
A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
 
#include <iostream>
const double pi = 3.14159265358979323846;
using namespace std;
 
// Function to find the equation
// of circle whose center is (x1, y1)
// and the radius of circle is r
void circleArea(double r)
{
    cout << (pi * r * r);
}
 
// Function to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
void findCircleAreaByMedian(double m)
{
    double r = 2 * m / 3;
 
    // Util Function to find the
    // circle equation
    circleArea(r);
}
 
// Driver code
int main()
{
    double m = 3;
 
    // Function Call
    findCircleAreaByMedian(m);
    return 0;
}

// Java implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
import java.util.*;
 
class GFG{
     
// Function to find the equation
// of circle whose center is (x1, y1)
// and the radius of circle is r
static double circleArea(double r)
{
    double pi = 3.14159265358979323846;
    return (pi * r * r);
}
     
// Function to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
static double findCircleAreaByMedian(int m)
{
    double r = 2 * m / 3;
     
    // Function call to find
    // the circle equation
    return circleArea(r);
}
 
// Driver code
public static void main(String args[])
{
    int m = 3;
     
    System.out.printf("%.4f", findCircleAreaByMedian(m));
}
}
 
// This code is contributed by virusbuddah_

# Python3 implementation to find the
# equation of circle which inscribes
# equilateral triangle of median M
 
pi = 3.14159265358979323846
 
# Function to find the equation
# of circle whose center is (x1, y1)
# and the radius of circle is r
def circleArea(r):
     
    print(round(pi * r * r, 4))
 
# Function to find the
# equation of circle which
# inscribes equilateral triangle
# of median M
def findCircleAreaByMedian(m):
     
    r = 2 * m /3
 
    # Function to find the
    # circle equation
    circleArea(r)
 
# Driver code
if __name__ == '__main__':
     
    m = 3
 
    # Function call
    findCircleAreaByMedian(m)
 
# This code is contributed by mohit kumar 29

// C# implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
using System;
 
class GFG{
     
// Function to find the equation
// of circle whose center is (x1, y1)
// and the radius of circle is r
static double circleArea(double r)
{
    double pi = 3.14159265358979323846;
    return (pi * r * r);
}
         
// Function to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
static double findCircleAreaByMedian(int m)
{
    double r = 2 * m / 3;
         
    // Function call to find
    // the circle equation
    return circleArea(r);
}
     
// Driver code
public static void Main(string []args)
{
    int m = 3;
         
    Console.WriteLine("{0:f4}", findCircleAreaByMedian(m));
}
}
 
// This code is contributed by AnkitRai01

<script>
// javascript implementation to find the
// equation of circle which
// inscribes equilateral triangle
// of median M
 
    // Function to find the equation
    // of circle whose center is (x1, y1)
    // and the radius of circle is r
    function circleArea(r) {
        var pi = 3.14159265358979323846;
        return (pi * r * r);
    }
 
    // Function to find the
    // equation of circle which
    // inscribes equilateral triangle
    // of median M
    function findCircleAreaByMedian(m) {
        var r = 2 * m / 3;
 
        // Function call to find
        // the circle equation
        return circleArea(r);
    }
 
    // Driver code
     
    var m = 3;
 
    document.write(findCircleAreaByMedian(m).toFixed(4));
 
// This code is contributed by Rajput-Ji
</script>

12.5664