Conteo de números hasta N dígitos formados usando dígitos 0 a K-1 sin ningún 0 adyacente

Dados dos números enteros N y K , la tarea es contar los números hasta N dígitos de modo que no haya dos ceros adyacentes y el rango de dígitos sea de 0 a K-1.
Ejemplos: 
 

Entrada: N = 2, K = 3 
Salida: 8 
Explicación: 
Hay 8 números tales que los dígitos son solo del 0 al 2, sin ningún 0 adyacente: {1, 2, 10, 11, 12, 20, 21, 22 }
Entrada: N = 3, K = 3 
Salida: 22 
 

Enfoque: La idea es utilizar Programación Dinámica para resolver este problema. 
Sea DP[i][j] el número de números deseables hasta el i-ésimo dígito del número, y su último dígito como j .
Observaciones:

• El número de formas de llenar un lugar es
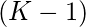
• Como sabemos, los ceros no pueden ser adyacentes. Entonces, cuando nuestro último elemento es 0, significa que el índice anterior se llena de 1 manera, es decir, 0. Por lo tanto, el lugar actual solo se puede llenar con (K-1) dígitos.
• Si el último lugar se llena con (K-1) dígitos, entonces el lugar del dígito actual se puede llenar con 0 o (K-1) dígitos.

Caso base:

• Si n == 1 y último == K, entonces podemos llenar este lugar con (K-1) dígitos, devolver (K-1)
• De lo contrario, devuelve 1

Relación de recurrencia:
 

Cuando el lugar del último dígito no se llena con cero, entonces 
 

 

Cuando el lugar del último dígito se llena con cero, entonces 
 

 

 

 

A continuación se muestra la implementación del enfoque anterior:
 

// C++ implementation to count the
// numbers upto N digits such that
// no two zeros are adjacent
 
#include <bits/stdc++.h>
using namespace std;
 
int dp[15][10];
 
// Function to count the
// numbers upto N digits such that
// no two zeros are adjacent
int solve(int n, int last, int k)
{
    // Condition to check if only
    // one element remains
    if (n == 1) {
 
        // If last element is non
        // zero, return K-1
        if (last == k) {
            return (k - 1);
        }
        // If last element is 0
        else {
            return 1;
        }
    }
 
    // Condition to check if value
    // calculated already
    if (dp[n][last])
        return dp[n][last];
 
    // If last element is non zero,
    // then two cases arise,
    // current element can be either
    // zero or non zero
    if (last == k) {
 
        // Memoize this case
        return dp[n][last]
               = (k - 1)
                     * solve(n - 1, k, k)
                 + (k - 1)
                       * solve(n - 1, 1, k);
    }
 
    // If last is 0, then current
    // can only be non zero
    else {
 
        // Memoize and return
        return dp[n][last]
               = solve(n - 1, k, k);
    }
}
 
// Driver Code
int main()
{
    // Given N and K
    int n = 2, k = 3;
 
    // Function Call
    int x = solve(n, k, k)
            + solve(n, 1, k);
    cout << x;
}

// Java implementation to count the
// numbers upto N digits such that
// no two zeros are adjacent
class GFG{
     
static int[][] dp = new int[15][10];
 
// Function to count the numbers
// upto N digits such that
// no two zeros are adjacent
static int solve(int n, int last, int k)
{
     
    // Condition to check if only
    // one element remains
    if (n == 1)
    {
         
        // If last element is non
        // zero, return K-1
        if (last == k)
        {
            return (k - 1);
        }
         
        // If last element is 0
        else
        {
            return 1;
        }
    }
 
    // Condition to check if
    // value calculated already
    if (dp[n][last] == 1)
        return dp[n][last];
 
    // If last element is non zero,
    // then two cases arise, current
    // element can be either zero
    // or non zero
    if (last == k)
    {
         
        // Memoize this case
        return dp[n][last] = (k - 1) *
                        solve(n - 1, k, k) +
                             (k - 1) *
                        solve(n - 1, 1, k);
    }
     
    // If last is 0, then current
    // can only be non zero
    else
    {
 
        // Memoize and return
        return dp[n][last] = solve(n - 1, k, k);
    }
}
 
// Driver Code
public static void main(String[] args)
{
     
    // Given N and K
    int n = 2, k = 3;
 
    // Function Call
    int x = solve(n, k, k) +
            solve(n, 1, k);
     
    System.out.print(x);
}
}
 
// This code is contributed by Ritik Bansal

# Python3 implementation to count the
# numbers upto N digits such that
# no two zeros are adjacent
dp = [[0] * 10 for j in range(15)]
 
# Function to count the numbers
# upto N digits such that no two
# zeros are adjacent
def solve(n, last, k):
 
    # Condition to check if only
    # one element remains
    if (n == 1):
 
        # If last element is non
        # zero, return K-1
        if (last == k):
            return (k - 1)
         
        # If last element is 0
        else:
            return 1
 
    # Condition to check if value
    # calculated already
    if (dp[n][last]):
        return dp[n][last]
 
    # If last element is non zero,
    # then two cases arise, current
    # element can be either zero or
    # non zero
    if (last == k):
 
        # Memoize this case
        dp[n][last] = ((k - 1) *
                  solve(n - 1, k, k) +
                       (k - 1) *
                  solve(n - 1, 1, k))
                        
        return dp[n][last]
 
    # If last is 0, then current
    # can only be non zero
    else:
 
        # Memoize and return
        dp[n][last] = solve(n - 1, k, k)
        return dp[n][last]
 
# Driver code
 
# Given N and K
n = 2
k = 3
 
# Function call
x = solve(n, k, k) + solve(n, 1, k)
 
print(x)
 
# This code is contributed by himanshu77

// C# implementation to count the
// numbers upto N digits such that
// no two zeros are adjacent
using System;
 
class GFG{
     
public static int [,]dp = new int[15, 10];
 
// Function to count the numbers
// upto N digits such that
// no two zeros are adjacent
public static int solve(int n, int last, int k)
{
     
    // Condition to check if only
    // one element remains
    if (n == 1)
    {
         
        // If last element is non
        // zero, return K-1
        if (last == k)
        {
            return (k - 1);
        }
         
        // If last element is 0
        else
        {
            return 1;
        }
    }
 
    // Condition to check if
    // value calculated already
    if (dp[n, last] == 1)
        return dp[n, last];
 
    // If last element is non zero,
    // then two cases arise, current
    // element can be either zero
    // or non zero
    if (last == k)
    {
         
        // Memoize this case
        return dp[n, last] = (k - 1) *
                        solve(n - 1, k, k) +
                             (k - 1) *
                        solve(n - 1, 1, k);
    }
     
    // If last is 0, then current
    // can only be non zero
    else
    {
 
        // Memoize and return
        return dp[n, last] = solve(n - 1, k, k);
    }
}
 
// Driver Code
public static void Main(string[] args)
{
     
    // Given N and K
    int n = 2, k = 3;
 
    // Function Call
    int x = solve(n, k, k) +
            solve(n, 1, k);
     
    Console.WriteLine(x);
}
}
 
// This code is contributed by SoumikMondal

<script>
 
// Javascript implementation to count the
// numbers upto N digits such that
// no two zeros are adjacent
 
var dp = Array.from(Array(15),
() => Array(10).fill(0));
 
// Function to count the
// numbers upto N digits such that
// no two zeros are adjacent
function solve(n, last, k)
{
    // Condition to check if only
    // one element remains
    if (n == 1) {
 
        // If last element is non
        // zero, return K-1
        if (last == k) {
            return (k - 1);
        }
        // If last element is 0
        else {
            return 1;
        }
    }
 
    // Condition to check if value
    // calculated already
    if ((dp[n][last])!=0)
        return dp[n][last];
 
    // If last element is non zero,
    // then two cases arise,
    // current element can be either
    // zero or non zero
    if (last == k) {
 
        // Memoize this case
        return dp[n][last]
               = (k - 1)
                     * solve(n - 1, k, k)
                 + (k - 1)
                       * solve(n - 1, 1, k);
    }
 
    // If last is 0, then current
    // can only be non zero
    else {
 
        // Memoize and return
        dp[n][last]
               = solve(n - 1, k, k);
        return dp[n][last];
    }
}
 
// Driver Code
// Given N and K
var n = 2, k = 3;
// Function Call
var x = solve(n, k, k)
        + solve(n, 1, k);
document.write(x);
 
 
</script>

8

Complejidad temporal: O(N)  
Espacio auxiliar: O(N*10)