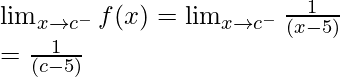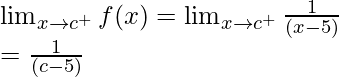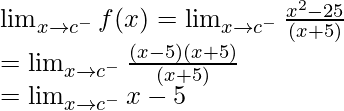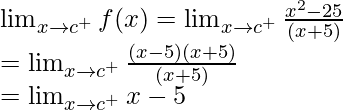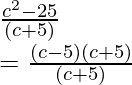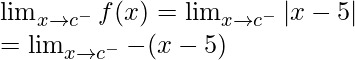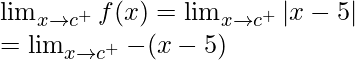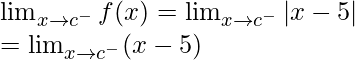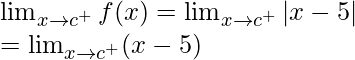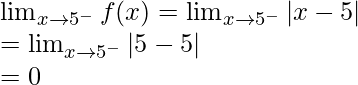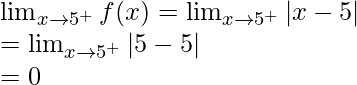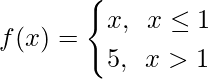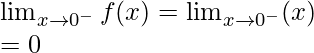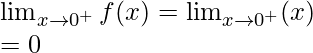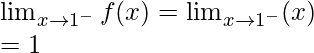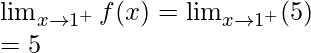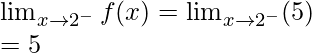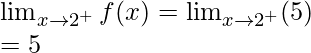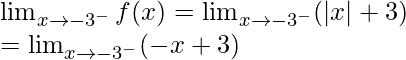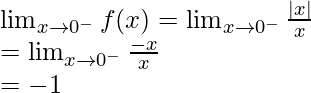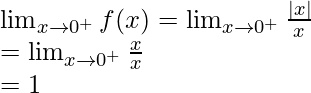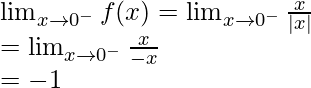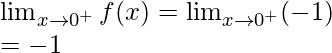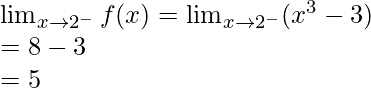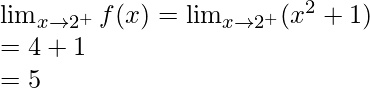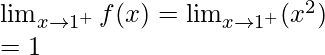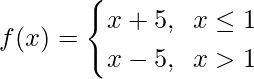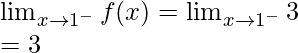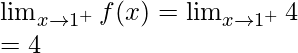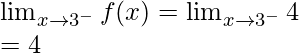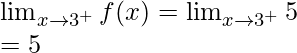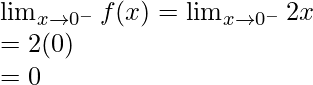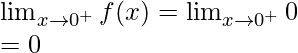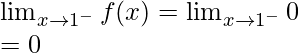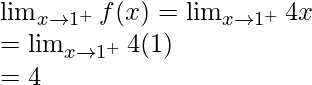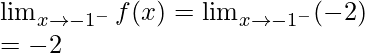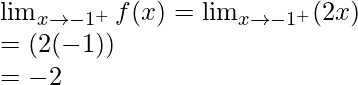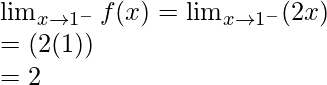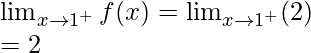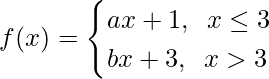Pregunta 1. Demuestra que la función f(x) = 5x – 3 es continua en x = 0, en x = – 3 y en x = 5.
Solución:
Para probar la continuidad de la función f(x) = 5x – 3, primero tenemos que calcular los límites y el valor de la función en ese punto.
Continuidad en x = 0
Límite izquierdo =
= (5(0) – 3) = -3
Límite derecho =
= (5(0) – 3)= -3
Valor de función en x = 0, f(0) = 5(0) – 3 = -3
como,
,
Por lo tanto, la función es continua en x = 0.
Continuidad en x = -3
Límite izquierdo =
= (5(-3) – 3) = -18
Límite derecho =
= (5(-3) – 3) = -18
Valor de la función en x = -3, f(-3) = 5(-3) – 3 = -18
Como,
Por tanto, la función es continua en x = -3.
Continuidad en x = 5
Límite izquierdo =
= (5(5) – 3) = 22
Límite derecho =
= (5(5) – 3) = 22
Valor de la función en x = 5, f(5) = 5(5) – 3 = 22
Como,
Por lo tanto, la función es continua en x = 5.
Pregunta 2. Examina la continuidad de la función f(x) = 2x 2 – 1 en x = 3.
Solución:
Para probar la continuidad de la función f(x) = 2x 2 – 1, primero tenemos que calcular los límites y el valor de la función en ese punto.
Continuidad en x = 3
Límite izquierdo =
= (2(3) 2 – 1) = 17
Límite derecho =
= (2(3) 2 – 1) = 17
Valor de función en x = 3, f(3) = 2(3) 2 – 1 = 17
Como,
Por lo tanto, la función es continua en x = 3.
Pregunta 3. Examine las siguientes funciones para la continuidad.
(a) f(x) = x – 5
Solución:
Para probar la continuidad de la función f(x) = x – 5, primero tenemos que calcular los límites y el valor de la función en ese punto.
Tomemos un número real, c
Continuidad en x = c
Límite izquierdo =
= (c – 5) = c – 5
Límite derecho =
= (c – 5) = c – 5
Valor de la función en x = c, f(c) = c – 5
Como,
para cualquier número real c
Por lo tanto, la función es continua en todo número real.
(b) 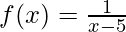 , x ≠ 5
, x ≠ 5
Solución:
Para probar la continuidad de la función f(x) =
, primero tenemos que calcular los límites y el valor de la función en ese punto.
Tomemos un número real, c
Continuidad en x = c y c ≠ 5
Límite izquierdo =
Límite derecho =
Valor de la función en x = c, f(c) =
Como,
para cualquier número real c
Por lo tanto, la función es continua en todo número real.
(c) 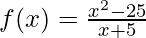 , x ≠ -5
, x ≠ -5
Solución:
Para probar la continuidad de la función f(x) =
, primero tenemos que calcular los límites y el valor de la función en ese punto.
Tomemos un número real, c
Continuidad en x = c y c ≠ -5
Límite izquierdo =
= c – 5
Límite derecho =
= c – 5
Valor de la función en x = c, f(c) =
= c – 5
Como,
, para cualquier número real c
Por lo tanto, la función es continua en todo número real.
(d) f(x) = |x – 5|
Solución:
Para probar la continuidad de la función f(x) = |x – 5|, primero tenemos que calcular los límites y el valor de la función en ese punto.
Aquí,
Como sabemos, la función de módulo funciona de manera diferente.
En |x – 5|, |x – 5| = x – 5 cuando x>5 y |x – 5| = -(x – 5) cuando x < 5
Tomemos un número real, c y busquemos tres casos de c:
Continuidad en x = c
Cuando c < 5
Límite izquierdo =
= -(c – 5)
= 5 – do
Límite derecho =
= -(c – 5)
= 5 – do
Valor de la función en x = c, f(c) = |c – 5| = 5 – do
Como,
Por tanto, la función es continua en todo número real c, donde c<5.
Cuando c > 5
Límite izquierdo =
= (c – 5)
Límite derecho =
= (c – 5)
Valor de la función en x = c, f(c) = |c – 5| = c – 5
como,
,
Por tanto, la función es continua en todo número real c, donde c > 5.
Cuando c = 5
Límite izquierdo =
Límite derecho =
Valor de la función en x = c, f(c) = |5 – 5| = 0
Como,
Por tanto, la función es continua en todo número real c, donde c = 5.
Por lo tanto, podemos concluir que la función de módulo es continua en todo número real.
Pregunta 4. Demuestre que la función f(x) = x n es continua en x = n, donde n es un número entero positivo.
Solución:
Para probar la continuidad de la función f(x) = x n , primero tenemos que calcular los límites y el valor de la función en ese punto.
Continuidad en x = n
Límite izquierdo =
= norte norte
Límite derecho =
= norte norte
Valor de la función en x = n, f(n) = n n
Como,
Por tanto, la función es continua en x = n.
Pregunta 5. ¿La función f está definida por
continua en x = 0? en x = 1? en x = 2?
Para probar la continuidad de la función f(x), primero tenemos que calcular los límites y el valor de la función en ese punto.
Continuidad en x = 0
Límite izquierdo =
Límite derecho =
Valor de función en x = 0, f(0) = 0
Como,
Por lo tanto, la función es continua en x = 0.
Continuidad en x = 1
Límite izquierdo =
Límite derecho =
Valor de función en x = 1, f(1) = 1
como,
,
Por tanto, la función no es continua en x = 1.
Continuidad en x = 2
Límite izquierdo =
Límite derecho =
Valor de la función en x = 2, f(2) = 5
como,
,
Por lo tanto, la función es continua en x = 2.
Encuentre todos los puntos de discontinuidad de f, donde f está definida por
Pregunta 6. 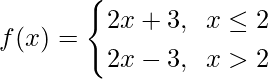
Solución:
Aquí, como se da que
Para x ≤ 2, f(x) = 2x + 3, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continuo x ∈ (-∞, 2)
Ahora, para x > 2, f(x) = 2x – 3, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continua x ∈ (2, ∞)
Ahora, como f(x) es continua en x ∈ (-∞, 2) U (2, ∞) = R – {2}
Verifiquemos la continuidad en x = 2,
Límite izquierdo =
= (2(2) + 3)
= 7
Límite derecho =
= (2(2) – 3)
= 1
Valor de función en x = 2, f(2) = 2(3) + 3 = 7
Como,
Por lo tanto, la función es discontinua en solo x = 2.
Pregunta 7. 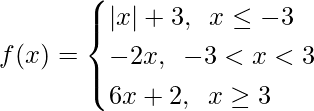
Solución:
Aquí, como se da que
Para x ≤ -3, f(x) = |x| + 3,
Como sabemos, la función de módulo funciona de manera diferente.
En |x|, |x – 0| = x cuando x > 0 y |x – 0| = -x cuando x < 0
f(x) = -x + 3, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continuo x ∈ (-∞, -3)
Para -3 < x < 3, f(x) = -2x, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continua x ∈ (-3, 3)
Ahora, para x ≥ 3, f(x) = 6x + 2, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continua x ∈ (3, ∞)
Entonces ahora, como f(x) es continua en x ∈ (-∞, -3) U(-3, 3) U (3, ∞) = R – {-3, 3}
Verifiquemos la continuidad en x = -3,
Límite izquierdo =
= (-(-3) + 3)
= 6
Límite derecho =
= (-2(-3))
= 6
Valor de la función en x = -3, f(-3) = |-3| + 3 = 3 + 3 = 6
Como,
Por tanto, la función es continua en x = -3.
Ahora, comprobemos la continuidad en x = 3,
Límite izquierdo =
= (-2(3))
= -6
Límite derecho =
= (6(3) + 2)
= 20
Valor de función en x = 3, f(3) = 6(3) + 2 = 20
Como,
Por lo tanto, la función es discontinua solo en x = 3.
pregunta 8 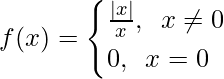
Solución:
Como sabemos, la función de módulo funciona de manera diferente.
En |x|, |x – 0| = x cuando x > 0 y |x – 0|= -x cuando x < 0
Cuando x < 0 , f(x) =
= -1, que es una constante
Como las funciones constantes son continuas, entonces f(x) es continua x ∈ (-∞, 0).
Cuando x > 0 , f(x) =
= 1, que es una constante
Como las funciones constantes son continuas, entonces f(x) es continua x ∈ (0, ∞).
Ahora, como f(x) es continua en x ∈ (-∞, 0) U(0, ∞) = R – {0}
Verifiquemos la continuidad en x = 0,
Límite izquierdo =
Límite derecho =
Valor de función en x = 0, f(0) = 0
Como,
Por lo tanto, la función es discontinua solo en x = 0.
Pregunta 9. 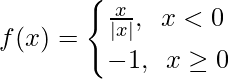
Solución:
Como sabemos, la función de módulo funciona de manera diferente.
En |x|, |x – 0| = x cuando x > 0 y |x – 0| = -x cuando x < 0
Cuando x < 0 , f(x) =
= -1, que es una constante
Como las funciones constantes son continuas, entonces f(x) es continua x ∈ (-∞, 0).
Cuando x > 0, f(x) = -1, que es una constante
Como las funciones constantes son continuas, entonces f(x) es continua x ∈ (0, ∞).
Ahora, como f(x) es continua en x ∈ (-∞, 0) U(0, ∞) = R – {0}
Verifiquemos la continuidad en x = 0,
Límite izquierdo =
Límite derecho =
Valor de la función en x = 0, f(0) = -1
Como,
Por lo tanto, la función es continua en x = 0.
Entonces, concluimos que f(x) es continua en cualquier número real. Por lo tanto, no hay punto de discontinuidad.
Pregunta 10. 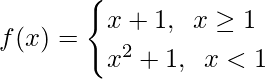
Solución:
Aquí,
Cuando x ≥1, f(x) = x + 1, que es un polinomio
Como las funciones polinomiales son continuas, entonces f(x) es continua x ∈ (1, ∞)
Cuando x < 1, f(x) = x 2 + 1, que es un polinomio
Como las funciones polinómicas son continuas, entonces f(x) es continua x ∈ (-∞, 1)
Entonces ahora, como f(x) es continua en x ∈ (-∞, 1) U (1, ∞) = R – {1}
Verifiquemos la continuidad en x = 1,
Límite izquierdo =
= 1 + 1
= 2
Límite derecho =
= 1 + 1
= 2
Valor de función en x = 1, f(1) = 1 + 1 = 2
Como,
Por lo tanto, la función es continua en x = 1.
Entonces, concluimos que f(x) es continua en cualquier número real.
Pregunta 11. 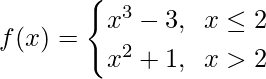
Solución:
Aquí,
Cuando x ≤ 2, f(x) = x 3 + 3, que es un polinomio
Como las funciones polinómicas son continuas, entonces f(x) es continua x ∈ (-∞, 2)
Cuando x > 2, f(x) = x 2 + 1, que es un polinomio
Como las funciones polinomiales son continuas, entonces f(x) es continua x ∈ (2, ∞)
Ahora, como f(x) es continua en x ∈ (-∞, 2) U(2, ∞) = R – {2}
Verifiquemos la continuidad en x = 2,
Límite izquierdo =
Límite derecho =
Valor de función en x = 2, f(2) = 8 – 3 = 5
Como,
Por lo tanto, la función es continua en x = 2.
Entonces, concluimos que f(x) es continua en cualquier número real.
Pregunta 12. 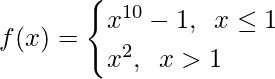
Solución:
Aquí,
Cuando x ≤ 1, f(x) = x 10 – 1, que es un polinomio
Como las funciones polinómicas son continuas, entonces f(x) es continua x ∈ (-∞, 1)
Cuando x >1, f(x) = x 2 , que es un polinomio
Como las funciones polinomiales son continuas, entonces f(x) es continua x ∈ (1, ∞)
Entonces ahora, como f(x) es continua en x ∈ (-∞, 1) U (1, ∞) = R – {1}
Verifiquemos la continuidad en x = 1,
Límite izquierdo =
= 1 – 1
= 0
Límite derecho =
Valor de la función en x = 1, f(1) = 1 – 1 = 0
Como,
Por lo tanto, la función es discontinua en x = 1.
Pregunta 13. ¿La función está definida por
una función continua?
Solución:
Aquí, como se da que
Para x ≤ 1, f(x) = x + 5, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continuo x ∈ (-∞, 1)
Ahora, para x > 1, f(x) = x – 5, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continua x ∈ (1, ∞)
Entonces ahora, como f(x) es continua en x ∈ (-∞, 1) U (1, ∞) = R – {1}
Verifiquemos la continuidad en x = 1,
Límite izquierdo =
= (1 + 5)
= 6
Límite derecho =
= (1 – 5)
= -4
Valor de función en x = 1, f(1) = 5 + 1 = 6
Como,
Por lo tanto, la función es continua solo para R – {1}.
Discuta la continuidad de la función f, donde f está definida por
Pregunta 14. 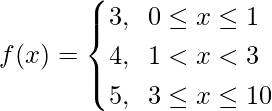
Solución:
Aquí, como se da que
Para 0 ≤ x ≤ 1, f(x) = 3, que es una constante
Como las constantes son continuas, entonces f(x) es continua x ∈ (0, 1)
Ahora, para 1 < x < 3, f(x) = 4, que es una constante
Como las constantes son continuas, entonces f(x) es continua x ∈ (1, 3)
Para 3 ≤ x ≤ 10, f(x) = 5, que es una constante
Como las constantes son continuas, entonces f(x) es continua x ∈ (3, 10)
Ahora, como f(x) es continua en x ∈ (0, 1) U (1, 3) U (3, 10) = (0, 10) – {1, 3}
Verifiquemos la continuidad en x = 1,
Límite izquierdo =
Límite derecho =
Valor de función en x = 1, f(1) = 3
Como,
Por lo tanto, la función es discontinua en x = 1.
Ahora, comprobemos la continuidad en x = 3,
Límite izquierdo =
Límite derecho =
Valor de la función en x = 3, f(3) = 4
Como,
Por lo tanto, la función es discontinua en x = 3.
Entonces, concluyendo los resultados, obtenemos
Por lo tanto, la función f(x) es discontinua en x = 1 y x = 3.
Pregunta 15. 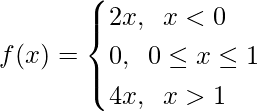
Solución:
Aquí, como se da que
Para x < 0, f(x) = 2x, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continuo x ∈ (-∞, 0)
Ahora, para 0 ≤ x ≤ 1, f(x) = 0, que es una constante
Como constantes son continuas, entonces f(x) es continua x ∈ (0, 1)
Para x > 1, f(x) = 4x, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continua x ∈ (1, ∞)
Ahora, como f(x) es continua en x ∈ (-∞, 0) U (0, 1) U (1, ∞)= R – {0, 1}
Verifiquemos la continuidad en x = 0,
Límite izquierdo =
Límite derecho =
Valor de función en x = 0, f(0) = 0
Como,
Por lo tanto, la función es continua en x = 0.
Ahora, comprobemos la continuidad en x = 1,
Límite izquierdo =
Límite derecho =
Valor de función en x = 1, f(1) = 0
Como,
Por lo tanto, la función es discontinua en x = 1.
Por lo tanto, la función es continua solo para R – {1}
Pregunta 16. 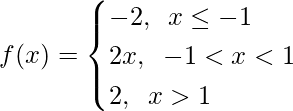
Solución:
Aquí, como se da que
Para x ≤ -1, f(x) = -2, que es una constante
Como constantes son continuas, por lo tanto f(x) es continua x ∈ (-∞, -1)
Ahora, para -1 ≤ x ≤ 1, f(x) = 2x, que es un polinomio
Como los polinomios son continuos, entonces f(x) es continuo x ∈ (-1, 1)
Para x > 1, f(x) = 2, que es una constante
Como constantes son continuas, luego f(x) es continua x ∈ (1, ∞)
Ahora, como f(x) es continua en x ∈ (-∞, -1) U (-1, 1) U (1, ∞)= R – {-1, 1}
Verifiquemos la continuidad en x = -1,
Límite izquierdo =
Límite derecho =
Valor de función en x = -1, f(-1) = -2
Como,
Por tanto, la función es continua en x = -1.
Ahora, comprobemos la continuidad en x = 1,
Límite izquierdo =
Límite derecho =
Valor de función en x = 1, f(1) = 2(1) = 2
Como,
Por lo tanto, la función es continua en x = 1.
Por lo tanto, la función es continua para cualquier número real.
Pregunta 17. Encuentra la relación entre a y b para que la función f definida por
es continua en x = 3.
Solución:
Como, se da que la función es continua en x = 3.
Debe satisfacer lo siguiente en x = 3:
Continuidad en x = 3,
Límite izquierdo =
= (a(3) + 1)
= 3a + 1
Límite derecho =
= (b(3) + 3)
= 3b + 3
Valor de la función en x = 3, f(3) = a(3) + 1 = 3a + 1
Igualando ambos límites, obtenemos
3a + 1 = 3b + 3
3(a – b) = 2
a-b = 2/3