Python | Transformación de Box-Cox

Imagina que estás viendo una carrera de caballos y, como en cualquier otra carrera, hay corredores rápidos y lentos. Entonces, lógicamente hablando, el caballo que llegó primero y los caballos rápidos junto con él tendrán la menor diferencia en el tiempo de finalización, mientras que los más lentos tendrán una mayor diferencia en el tiempo de finalización. 

Podemos relacionar esto con un término muy famoso en estadística llamado varianza , que se refiere a cuánto varían los datos con respecto a la media. Aquí, en nuestro ejemplo, hay una variación inconsistente (heterocedasticidad) entre los caballos rápidos y los caballos lentos porque habrá pequeñas variaciones para tiempos de finalización más cortos y viceversa. 

Por lo tanto, la distribución de nuestros datos no será una curva de campana ni una distribución normal, ya que habrá una cola más larga en el lado derecho. Estos tipos de distribuciones siguen la ley de potencia o la regla 80-20 donde el cambio relativo en una cantidad varía como la potencia de otra. En el gráfico anterior, podemos ver la distribución de la ley de potencia que alcanza su punto máximo para tiempos de ejecución cortos debido a la pequeña varianza y la cola pesada debido a tiempos de ejecución más largos. Estas distribuciones de ley de potencias se encuentran en el campo de la física, la biología, la economía, etc. 

Entonces, solo piense por un segundo que si estas distribuciones se encuentran en tantos campos, ¿qué pasaría si pudiéramos transformarlas en una distribución mucho más cómoda como la distribución normal? Eso nos facilitaría mucho la vida. Afortunadamente, tenemos una forma de transformar la ley de potencia o cualquier distribución no lineal en normal mediante una transformación de Box-Cox.

Pensemos intuitivamente que si tuviéramos que hacer esto para transformarnos, ¿cómo procederíamos? 

Está claro a partir de la figura que se muestra arriba que si de alguna manera pudiéramos inflar la variabilidad para el lado izquierdo de la distribución no normal, es decir, el pico y reducir la variabilidad en las colas. En resumen, tratando de mover el pico hacia el centro, podemos obtener una curva cercana a la curva en forma de campana. 

Formalmente, la transformación A Box cox se define como una forma de transformar las variables dependientes no normales en nuestros datos a una forma normal a través de la cual podemos ejecutar muchas más pruebas de las que podríamos tener. 

Matemáticas detrás de la transformación de Box-Cox: ¿Cómo podemos convertir nuestro pensamiento intuitivo en una función de transformación matemática? La transformación logarítmica es todo lo que necesitamos. Cuando se aplica una transformación logarítmica a una distribución no normal, intenta expandir las diferencias entre los valores más pequeños porque la pendiente de la función logarítmica es más pronunciada para los valores más pequeños, mientras que las diferencias entre los valores más grandes se pueden reducir porque, para los valores más grandes, la distribución de troncos tiene una pendiente moderada. Eso es lo que pensamos hacer, ¿verdad? La transformación de Box-cox solo se preocupa por calcular el valor de  que varía de – 5 a 5. Se  dice que un valor de es mejor si es capaz de aproximar la curva no normal a una curva normal. La ecuación de transformación es la siguiente: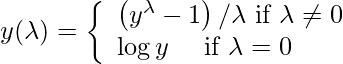Esta función requiere que la entrada sea positiva. Usar esta fórmula manualmente es una tarea muy laboriosa, por lo que muchas bibliotecas populares brindan esta función.

Implementación: el paquete de estadísticas de SciPy proporciona una función llamada boxcox para realizar la transformación de potencia box-cox que toma datos no normales originales como entrada y devuelve datos ajustados junto con el valor lambda que se usó para ajustar la distribución no normal a la distribución normal. A continuación se muestra el código para el mismo. 

Ejemplo: 

# Python3 code to show Box-cox Transformation
# of non-normal data
 
# import modules
import numpy as np
from scipy import stats
 
# plotting modules
import seaborn as sns
import matplotlib.pyplot as plt
 
# generate non-normal data (exponential)
original_data = np.random.exponential(size = 1000)
 
# transform training data & save lambda value
fitted_data, fitted_lambda = stats.boxcox(original_data)
 
# creating axes to draw plots
fig, ax = plt.subplots(1, 2)
 
# plotting the original data(non-normal) and
# fitted data (normal)
sns.distplot(original_data, hist = False, kde = True,
            kde_kws = {'shade': True, 'linewidth': 2},
            label = "Non-Normal", color ="green", ax = ax[0])
 
sns.distplot(fitted_data, hist = False, kde = True,
            kde_kws = {'shade': True, 'linewidth': 2},
            label = "Normal", color ="green", ax = ax[1])
 
# adding legends to the subplots
plt.legend(loc = "upper right")
 
# rescaling the subplots
fig.set_figheight(5)
fig.set_figwidth(10)
 
print(f"Lambda value used for Transformation: {fitted_lambda}")

Salida: podemos ver que la distribución no normal se convirtió en una distribución normal o más bien cercana a la normal usando SciPy.stats.boxcox(). ¿Box-cox siempre funciona? La respuesta es NO . Box-cox no garantiza la normalidad porque nunca comprueba la normalidad que es necesaria para ser infalible de que ha transformado correctamente la distribución no normal o no. Solo comprueba la desviación estándar más pequeña. 

Por lo tanto, es absolutamente necesario comprobar siempre la normalidad de los datos transformados mediante un gráfico de probabilidad.