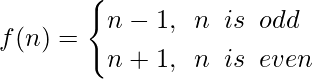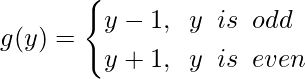Pregunta 1. Sea f : R → R definida como f(x) = 10x + 7. Halle la función g : R → R tal que gof = fog = 1 R .
Solución:
Como se menciona aquí
f : R → R se define como f(x) = 10x + 7
Demostrar la función uno a uno
Tomemos f(x) = f(y)
10x + 7 = 10y + 7
x = y
Por lo tanto f es uno-uno.
Demostrar la función en
y ∈ R, y = 10x+7
Entonces, significa que para y ∈ R, existe
Por tanto, f es sobre.
Como, f es uno-uno y sobre. Esta f es una función invertible.
Digamos que g : R → R se define como
Por tanto, g : R → R tal que gof = niebla = 1 R .
g : R → R se define como
Pregunta 2. Sea f : W → W definida como f(n) = n – 1, si n es impar y f(n) = n + 1, si n es par. Demuestre que f es invertible. Encuentra el inverso de f. Aquí, W es el conjunto de todos los números enteros.
Solución:
La función f se define como
Como sabemos que f es invertible, si y solo si f es uno-uno y sobre.
UNO UNO
Para el par de números, nos ocuparemos de tres casos:
Caso 1 : Cuando ambos números p y q son números impares.
f(p) = p-1
f(q) = q-1
f(p) = f(q)
p-1 = q-1
p-q = 0
Caso 2 : Cuando ambos números p y q son números pares.
f(p) = p+1
f(q) = q+1
f(p) = f(q)
p+1 = q+1
p-q = 0
Caso 3: Cuando p es impar y q es par
f(p) = p-1
f(q) = q+1
f(p) = f(q)
p-1 = q+1
p-q = 2
Restar un número impar y par siempre da un número impar, no par. Por lo tanto, el resultado del caso 3 es imposible.
Entonces, la función f es uno a uno, solo para el caso 1 y el caso 2.
SOBRE
Caso 1 : cuando p es un número impar
f(p) = p-1
y = p-1
pag = y+1
Por tanto, cuando p es impar y es par.
Caso 2 : Cuando p es un número par
f(p) = p+1
y = p+1
p = y-1
Por tanto, cuando p es par y es impar.
Entonces, significa que para y ∈ W, existe p = y+1 e y-1 para valores pares e impares de p respectivamente.
Por tanto, f es sobre.
Como, f es uno-uno y sobre. Esta f es una función invertible.
Digamos que g : W → W se define como
f = gramo
Por lo tanto, el inverso de f es f en sí mismo
Pregunta 3. Si f : R → R está definida por f(x) = x 2 – 3x + 2, encuentre f (f(x)).
Solución:
f(x) = x2 – 3x + 2
f(f(x)) = f(x 2 – 3x + 2)
= (x2 – 3x + 2 )2 – 3(x2 – 3x + 2 ) + 2
= x 4 + 9x 2 + 4 -6x 3 – 12x + 4x 2 – 3x 2 + 9x – 6 + 2
f(f(x)) = x 4 – 6x 3 + 10x 2 – 3x
Pregunta 4. Demostrar que la función f : R → {x ∈ R : – 1 < x < 1} definida por f(x) = 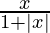 , x ∈ R es una función uno y sobre.
, x ∈ R es una función uno y sobre.
Solución:
Como se menciona aquí
f : R → {x ∈ R : – 1 < x < 1} definido por
, x ∈ R
Como sabemos que f es invertible, si y solo si f es uno-uno y sobre.
UNO UNO
Para el par de números, nos ocuparemos de tres casos:
Caso 1: Cuando ambos números p y p son números positivos.
La función f se define como
Caso 1 : Cuando ambos números p y q son números positivos.
f(p) = f(q)
p(1+q) = q(1+p)
p = q
Caso 2 : Cuando el número p y q son números negativos.
f(p) = f(q)
p(1-q) = q(1-p)
p = q
Caso 3 : Cuando p es positivo y q es negativo
f(p) = f(q)
p(1-q) = q(1+p)
p + q = 2pq
Aquí, RHS será negativo y LHS será positivo. Por lo tanto, el resultado del caso 3 es imposible.
Entonces, la función f es uno-uno, para el caso 1 y el caso 2.
SOBRE
Caso 1 : Cuando p>0.
Caso 2 : Cuando p <0
Por tanto, p está definida para todos los valores de y, p∈ R
Por tanto, f es sobre.
Como, f es uno-uno y sobre. Esta f es una función invertible.
Pregunta 5. Demostrar que la función f : R → R dada por f(x) = x 3 es inyectiva.
Solución:
Como se menciona aquí
f : R → R definida por f(x) = x 3 , x ∈ R
Demostrar que f es inyectiva (o uno-uno).
UNO UNO
La función f se define como
f(x) = x3
f(y) = y 3
f(x) = f(y)
x 3 = y 3
x = y
La función f es uno-uno, entonces f es inyectiva.
Pregunta 6. Da ejemplos de dos funciones f : N → Z y g : Z → Z tales que gof es inyectiva pero g no es inyectiva.
(Sugerencia: Considere f(x) = x y g (x) = | x |).
Solución:
Dos funciones, f : N → Z y g : Z → Z
Tomando f(x) = x y g(x) = |x|
Comprobemos si g es inyectiva o no.
g(5) = |5| = 5
g(-5) = |-5| = 5
Como podemos ver aquí que
Tomando dos enteros, 5 y -5
gramo(5) = gramo(-5)
pero, 5 ≠ -5
Entonces, g no es una función inyectiva.
Ahora, gof: N → Z se define como
gof = g(f(x)) = g(x) = |x|
Ahora, como x,y∈ N
g(x) = |x|
g(y) = |y|
g(x) = g(y)
|x| = |y|
x = y (tanto x como y son positivos)
Por lo tanto, gof es una inyectiva.
Pregunta 7. Dé ejemplos de dos funciones f : N → N yg : N → N tales que gof es sobre pero f no es sobre.
(Sugerencia: Considere f(x) = x + 1 y 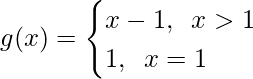
Solución:
Dos funciones, f : N → N y g : N → N
Tomando f(x) = x+1 y
Como, f(x) = x+1
y = x+1
x = y-1
Pero, cuando y=1, x = 0. Lo cual no satina esta relación f : N → N.
Por eso. f no es una función sobre.
Ahora, gof: N → N se define como
gof = g(f(x)) = g(x+1)
Cuando x+1=1, tenemos
g(x+1) = 1 (1∈ N)
Y, cuando x+1>1, tenemos
g(x+1) = (x+1)-1 = x
y = x, que también satisface x,y∈ N
Por lo tanto, gof es sobre.
Pregunta 8. Dado un conjunto X no vacío, considere P(X) que es el conjunto de todos los subconjuntos de X.
Defina la relación R en P(X) como sigue: Para los subconjuntos A, B en P(X), ARB si y solo si A ⊂ B. ¿Es R una relación de equivalencia en P(X)? Justifica tu respuesta.
Solución:
Dado, A y B son los subconjuntos de P(x), A⊂ B
Para comprobar la relación de equivalencia en P(X), tenemos que comprobar
- Reflexivo
Como sabemos que todo conjunto es el subconjunto de sí mismo.
Por lo tanto, A⊂ A y B⊂ B
ARA y BRB es reflexivo para todo A,B∈ P(X)
- Simétrico
Como, se da que A⊂ B. Pero no asegura que B⊂ A.
Para ser simétrico tiene que ser A = B
ARB no es simétrico.
- Transitivo
Cuando A⊂ B y B⊂ C
Entonces, por supuesto, A⊂ C
Por tanto, R es transitiva.
Entonces, como R no es simétrico.
R no es una relación de equivalencia en P(X).
Pregunta 9. Dado un conjunto no vacío X, considere la operación binaria ∗ : P(X) × P(X) → P(X) dada por A ∗ B = A ∩ B ∀ A, B en P(X), donde P(X) es el conjunto potencia de X. Demuestre que X es el elemento identidad para esta operación y X es el único elemento invertible en P(X) con respecto a la operación ∗.
Solución:
Dado, P(X) × P(X) → P(X) se define como A*B = A∩B ∀ A, B ∈ P(X)
Esto implica, A⊂ X y B ⊂ X
Entonces, A∩X = A y B∩X = B ∀ A, B ∈ P(X)
⇒ A*X = A y B*X = B
Por lo tanto, X es el elemento de identidad para la intersección del operador binario.
Pregunta 10. Encuentra el número de todas las funciones del conjunto {1, 2, 3, … , n} a sí mismo.
Solución:
Sobre la función del conjunto {1,2,3,…..,n} a sí mismo es igual que las permutaciones de n.
1×2×3×4×…….×n
que es n!.
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA