Programa para hallar la longitud del Latus Rectum de una Hipérbola

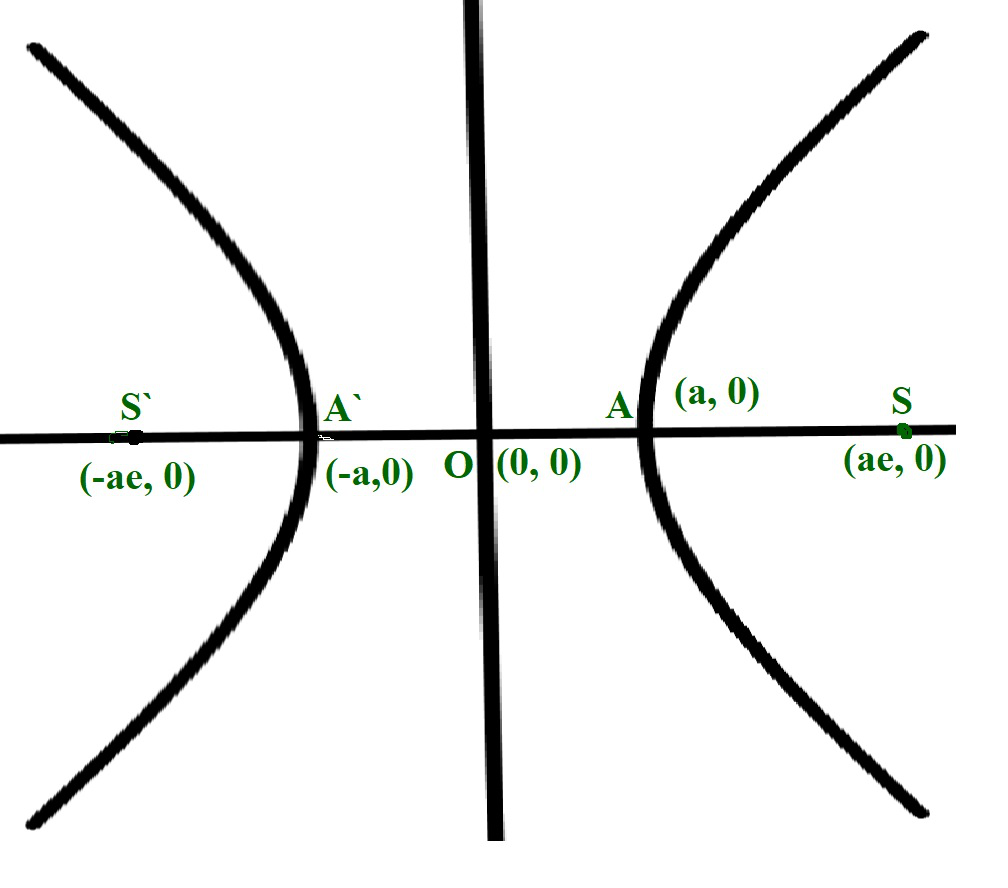
Dados dos números enteros A y B , que representan la longitud de los ejes semi-mayor y semi-menor de una hipérbola , la tarea es encontrar la longitud del lado recto de la hipérbola.

Ejemplos:

Entrada: A = 3, B = 2
Salida: 2.66666

Entrada: A = 6, B = 3
Salida: 3

Aproximación: El Latus Rectum de una hipérbola es la cuerda focal perpendicular al eje mayor y la longitud del Latus Rectum es igual a (Longitud del eje menor) ² /(longitud del eje mayor).

Siga los pasos a continuación para resolver el problema dado:

• Encuentre la longitud del eje mayor de la hipérbola y guárdela en una variable, digamos mayor .
• Encuentre la longitud del eje menor de la hipérbola y guárdela en una variable, digamos minor .
• Después de completar los pasos anteriores, imprima el valor de (menor*menor)/mayor como la longitud resultante del Latus Rectum.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <iostream>
using namespace std;
 
// Function to calculate the length of
// the latus rectum of a hyperbola
double lengthOfLatusRectum(double A,
                           double B)
{
    // Store the length of major axis
    double major = 2.0 * A;
 
    // Store the length of minor axis
    double minor = 2.0 * B;
 
    // Store the length of the
    // latus rectum
    double latus_rectum = (minor * minor)
                          / major;
 
    // Return the length of the
    // latus rectum
    return latus_rectum;
}
 
// Driver Code
int main()
{
    double A = 3.0, B = 2.0;
    cout << lengthOfLatusRectum(A, B);
 
    return 0;
}

// Java program for the above approach
import java.io.*;
 
class GFG{
   
// Function to calculate the length of
// the latus rectum of a hyperbola
static double lengthOfLatusRectum(double A,
                                  double B)
{
     
    // Store the length of major axis
    double major = 2.0 * A;
 
    // Store the length of minor axis
    double minor = 2.0 * B;
 
    // Store the length of the
    // latus rectum
    double latus_rectum = (minor * minor) / major;
 
    // Return the length of the
    // latus rectum
    return latus_rectum;
}
 
// Driver Code
public static void main(String[] args)
{
    double A = 3.0, B = 2.0;
     
    System.out.println(lengthOfLatusRectum(A, B));
}}
 
// This code is contributed by Dharanendra L V.

# Python program for the above approach
 
# Function to calculate the length of
# the latus rectum of a hyperbola
def lengthOfLatusRectum(A,B):
     
    # Store the length of major axis
    major = 2.0 * A
     
    # Store the length of minor axis   
    minor = 2.0 * B
     
    # Store the length of the
    # latus rectum
    latus_rectum = (minor * minor) / major
     
    # Return the length of the
    # latus rectum
    return latus_rectum
 
# Driver Code
A = 3.0
B = 2.0
print(round(lengthOfLatusRectum(A, B),5))
 
# This code is contributed by avanitrachhadiya2155

// C# program for the above approach
using System;
class GFG
{
 
// Function to calculate the length of
// the latus rectum of a hyperbola
static double lengthOfLatusRectum(double A,
                           double B)
{
   
    // Store the length of major axis
    double major = 2.0 * A;
 
    // Store the length of minor axis
    double minor = 2.0 * B;
 
    // Store the length of the
    // latus rectum
    double latus_rectum = (minor * minor)
                          / major;
 
    // Return the length of the
    // latus rectum
    return latus_rectum;
}
 
// Driver Code
public static void Main ()
{
    double A = 3.0, B = 2.0;
    Console.WriteLine(lengthOfLatusRectum(A, B));
 
}}
 
// This code is contributed by ukasp.

<script>
 
// Javascript program for the above approach
  
// Function to calculate the length of
// the latus rectum of a hyperbola
function lengthOfLatusRectum(A, B)
{
     
    // Store the length of major axis
    var major = 2.0 * A;
 
    // Store the length of minor axis
    var minor = 2.0 * B;
 
    // Store the length of the
    // latus rectum
    var latus_rectum = (minor * minor) / major;
 
    // Return the length of the
    // latus rectum
    return latus_rectum;
}
 
// Driver Code
var A = 3.0, B = 2.0;
 
document.write(lengthOfLatusRectum(A, B));
 
// This code is contributed by 29AjayKumar
 
</script>

2.66667

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)