Programa para encontrar la excentricidad de una hipérbola

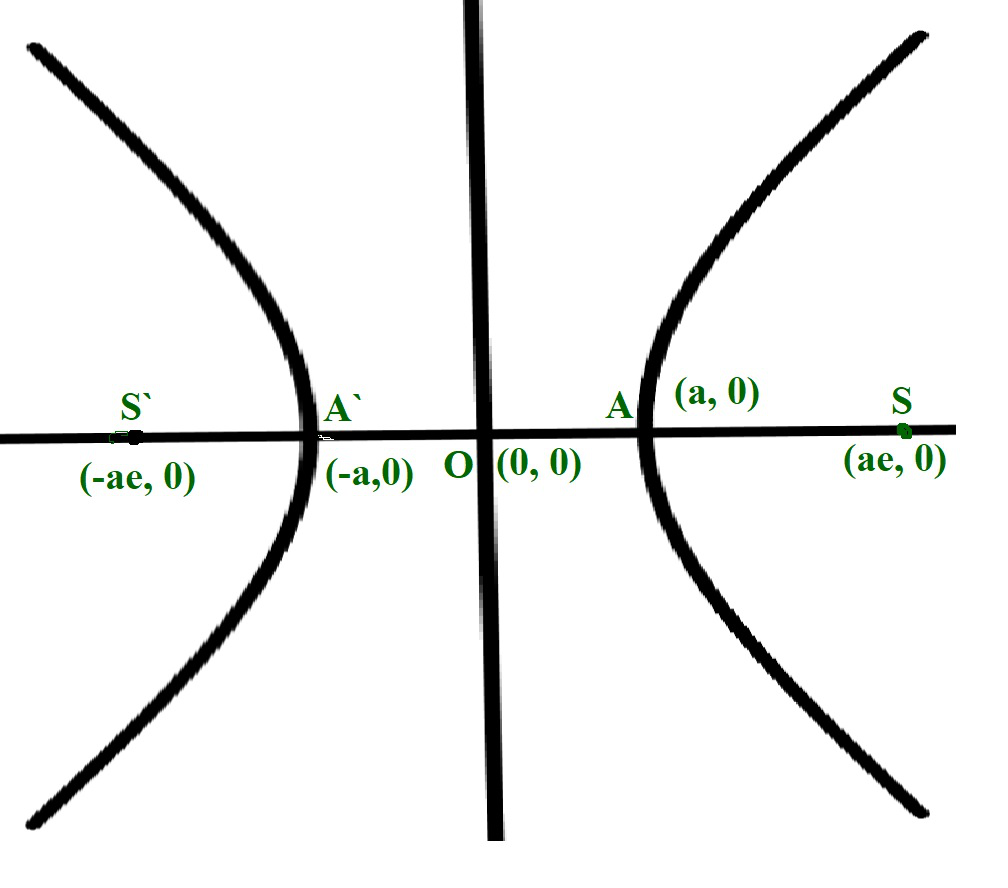
Dados dos números enteros A y B , que representan la longitud del eje semi-mayor y semi-menor de una Hipérbola de la ecuación (X ² / A ² ) – (Y ² / B ² ) = 1 , la tarea es calcular el excentricidad de la hipérbola dada.

Ejemplos:

Entrada: A = 3, B = 2
Salida: 1.20185
Explicación:
La excentricidad de la hipérbola dada es 1.20185.

Entrada: A = 6, B = 3
Salida: 1.11803

Enfoque: El problema dado se puede resolver usando la fórmula para encontrar la excentricidad de una elipse .

• La longitud del semieje mayor es A .
• La longitud del semieje menor es B .
• Por tanto, la excentricidad de la elipse viene dada por 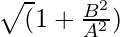  donde A > B

Por lo tanto, la idea es imprimir el valor de   como la excentricidad de la elipse.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the eccentricity
// of a hyperbola
double eccHyperbola(double A, double B)
{
    // Stores the squared ratio
    // of major axis to minor axis
    double r = (double)B * B / A * A;
 
    // Increment r by 1
    r += 1;
 
    // Return the square root of r
    return sqrt(r);
}
 
// Driver Code
int main()
{
    double A = 3.0, B = 2.0;
    cout << eccHyperbola(A, B);
 
    return 0;
}

// Java program for the above approach
import java.util.*;
 
class GFG{
 
// Function to find the eccentricity
// of a hyperbola
static double eccHyperbola(double A, double B)
{
     
    // Stores the squared ratio
    // of major axis to minor axis
    double r = (double)B * B / A * A;
 
    // Increment r by 1
    r += 1;
 
    // Return the square root of r
    return Math.sqrt(r);
}
 
// Driver Code
public static void main(String[] args)
{
    double A = 3.0, B = 2.0;
     
    System.out.print(eccHyperbola(A, B));
}
}
 
// This code is contributed by Amit Katiyar

# Python3 program for the above approach
import math
 
# Function to find the eccentricity
# of a hyperbola
 
 
def eccHyperbola(A, B):
 
    # Stores the squared ratio
    # of major axis to minor axis
    r = B * B / A * A
 
    # Increment r by 1
    r += 1
 
    # Return the square root of r
    return math.sqrt(r)
 
 
# Driver Code
if __name__ == "__main__":
 
    A = 3.0
    B = 2.0
    print(eccHyperbola(A, B))
 
    # This code is contributed by ukasp

// C# program for the above approach
using System;
 
class GFG{
 
// Function to find the eccentricity
// of a hyperbola
static double eccHyperbola(double A, double B)
{
     
    // Stores the squared ratio
    // of major axis to minor axis
    double r = (double)B * B / A * A;
 
    // Increment r by 1
    r += 1;
 
    // Return the square root of r
    return Math.Sqrt(r);
}
 
// Driver Code
public static void Main(String[] args)
{
    double A = 3.0, B = 2.0;
     
    Console.Write(eccHyperbola(A, B));
}
}
 
// This code is contributed by Princi Singh

<script>
 
// Javascript program for the above approach
 
// Function to find the eccentricity
// of a hyperbola
function eccHyperbola(A, B)
{
     
    // Stores the squared ratio
    // of major axis to minor axis
    let r = B * B / A * A;
 
    // Increment r by 1
    r += 1;
 
    // Return the square root of r
    return Math.sqrt(r);
}
 
// Driver Code
let A = 3.0;
let B = 2.0;
 
document.write(eccHyperbola(A, B));
 
// This code is contributed by mohit kumar
 
</script>

2.23607

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)