Dado un entero positivo n . El problema es encontrar la suma de la serie dada 1 + (1+2) + (1+2+3) + (1+2+3+4) + …… + (1+2+3+4+… +n) , donde el i-ésimo término de la serie es la suma de los primeros i números naturales impares.
Ejemplos:
Input : n = 2 Output : 5 (1) + (1+3) = 5 Input : n = 5 Output : 55 (1) + (1+3) + (1+3+5) + (1+3+5+7) + (1+3+5+7+9) = 55
Enfoque ingenuo: usando dos bucles, obtenga la suma de cada i-ésimo término y luego agregue esa suma a la suma final.
C++
// C++ implementation to find the
// sum of the given series
#include <bits/stdc++.h>
using namespace std;
// functionn to find the
// sum of the given series
int sumOfTheSeries(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++) {
// first term of each i-th term
int k = 1;
for (int j = 1; j <= i; j++) {
sum += k;
// next term
k += 2;
}
}
// required sum
return sum;
}
// Driver program
int main()
{
int n = 5;
cout << "Sum = "
<< sumOfTheSeries(n);
return 0;
}
Java
// Java implementation to find
// the sum of the given series
import java.util.*;
class GFG {
// functionn to find the sum
// of the given series
static int sumOfTheSeries(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
{
// first term of each
// i-th term
int k = 1;
for (int j = 1; j <= i; j++)
{
sum += k;
// next term
k += 2;
}
}
// required sum
return sum;
}
/* Driver program */
public static void main(String[] args)
{
int n = 5;
System.out.println("Sum = " +
sumOfTheSeries(n));
}
}
// This code is contributed by Arnav Kr. Mandal.
Python3
# Python3 implementation to find
# the sum of the given series
# functionn to find the sum
# of the given series
def sumOfTheSeries( n ):
sum = 0
for i in range(1, n + 1):
# first term of each i-th term
k = 1
for j in range(1,i+1):
sum += k
# next term
k += 2
# required sum
return sum
# Driver program
n = 5
print("Sum =", sumOfTheSeries(n))
# This code is contributed by "Sharad_Bhardwaj".
C#
// C# implementation to find
// the sum of the given series
using System;
class GFG {
// functionn to find the sum
// of the given series
static int sumOfTheSeries(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++) {
// first term of each
// i-th term
int k = 1;
for (int j = 1; j <= i; j++) {
sum += k;
// next term
k += 2;
}
}
// required sum
return sum;
}
/* Driver program */
public static void Main()
{
int n = 5;
Console.Write("Sum = " +
sumOfTheSeries(n));
}
}
// This code is contributed by vt_m.
php
<?php
// php implementation to find the
// sum of the given series
// functionn to find the
// sum of the given series
function sumOfTheSeries($n)
{
$sum = 0;
for ($i = 1; $i <= $n; $i++) {
// first term of each i-th term
$k = 1;
for ($j = 1; $j <= $i; $j++) {
$sum += $k;
// next term
$k += 2;
}
}
// required sum
return $sum;
}
// Driver program
$n = 5;
echo "Sum = "
. sumOfTheSeries($n);
// This code is contributed by Sam007
?>
Javascript
<script>
// Javascript implementation to find the
// sum of the given series
// functionn to find the
// sum of the given series
function sumOfTheSeries(n)
{
let sum = 0;
for (let i = 1; i <= n; i++) {
// first term of each i-th term
let k = 1;
for (let j = 1; j <= i; j++) {
sum += k;
// next term
k += 2;
}
}
// required sum
return sum;
}
// Driver program
let n = 5;
document.write("Sum = " + sumOfTheSeries(n));
// This code is contributed by gfgking
</script>
Producción:
Sum = 55
Enfoque eficiente:
Sea a n el término n-ésimo de la serie dada.
an = (1 + 3 + 5 + 7 + (2n-1)) = sum of first n odd numbers = n2
Consulte esta publicación para ver la prueba de la fórmula anterior.
Ahora,
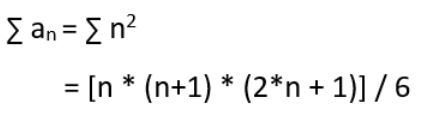
Consulte esta publicación para ver la prueba de la fórmula anterior.
C++
// C++ implementation to find the sum
// of the given series
#include <bits/stdc++.h>
using namespace std;
// functionn to find the sum
// of the given series
int sumOfTheSeries(int n)
{
// required sum
return (n * (n + 1) / 2) *
(2 * n + 1) / 3;
}
// Driver program to test above
int main()
{
int n = 5;
cout << "Sum = "
<< sumOfTheSeries(n);
return 0;
}
Java
// Java implementation to find
// the sum of the given series
import java.io.*;
class GfG {
// function to find the sum
// of the given series
static int sumOfTheSeries(int n)
{
// required sum
return (n * (n + 1) / 2) *
(2 * n + 1) / 3;
}
// Driver program to test above
public static void main (String[] args)
{
int n = 5;
System.out.println("Sum = "+
sumOfTheSeries(n));
}
}
// This code is contributed by Gitanjali.
Python3
# Python3 implementation to find
# the sum of the given series
# functionn to find the sum
# of the given series
def sumOfTheSeries( n ):
# required sum
return int((n * (n + 1) / 2) *
(2 * n + 1) / 3)
# Driver program to test above
n = 5
print("Sum =", sumOfTheSeries(n))
# This code is contributed by "Sharad_Bhardwaj".
C#
// C# implementation to find
// the sum of the given series
using System;
class GfG {
// function to find the sum
// of the given series
static int sumOfTheSeries(int n)
{
// required sum
return (n * (n + 1) / 2) *
(2 * n + 1) / 3;
}
// Driver program to test above
public static void Main()
{
int n = 5;
Console.Write("Sum = " +
sumOfTheSeries(n));
}
}
// This code is contributed by vt_m.
PHP
<?php
// PHP implementation to find the sum
// of the given series
// functionn to find the sum
// of the given series
function sumOfTheSeries($n)
{
// required sum
return ($n * ($n + 1) / 2) *
(2 * $n + 1) / 3;
}
// Driver Code
$n = 5;
echo "Sum = "
. sumOfTheSeries($n);
// This code is contributed by Sam007
?>
Javascript
<script>
// JavaScript program to find
// the sum of the given series
// function to find the sum
// of the given series
function sumOfTheSeries(n)
{
// required sum
return (n * (n + 1) / 2) *
(2 * n + 1) / 3;
}
// Driver Code
let n = 5;
document.write("Sum = " +
sumOfTheSeries(n));
// This code is contributed by avijitmondal1998.
</script>
Producción:
Sum = 55
Publicación traducida automáticamente
Artículo escrito por ayushjauhari14 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA