Análisis de la complejidad de la búsqueda binaria

Complejidades como O(1) y O(n) son fáciles de entender. O(1) significa que requiere un tiempo constante para realizar operaciones como llegar a un elemento en un tiempo constante como en el caso del diccionario y O(n) significa que depende del valor de n para realizar operaciones como buscar un elemento en una array de n elementos. 

Pero para O(Log n) , no es tan simple. Analicemos esto con la ayuda del algoritmo de búsqueda binaria cuya complejidad es O(log n) . 

Búsqueda binaria: busque una array ordenada dividiendo repetidamente el intervalo de búsqueda por la mitad. Comience con un intervalo que cubra todo el arreglo. Si el valor de la clave de búsqueda es menor que el elemento en el medio del intervalo, reduzca el intervalo a la mitad inferior. De lo contrario, redúcelo a la mitad superior. Verifique repetidamente hasta que se encuentre el valor o el intervalo esté vacío. 

Ejemplo: 
 

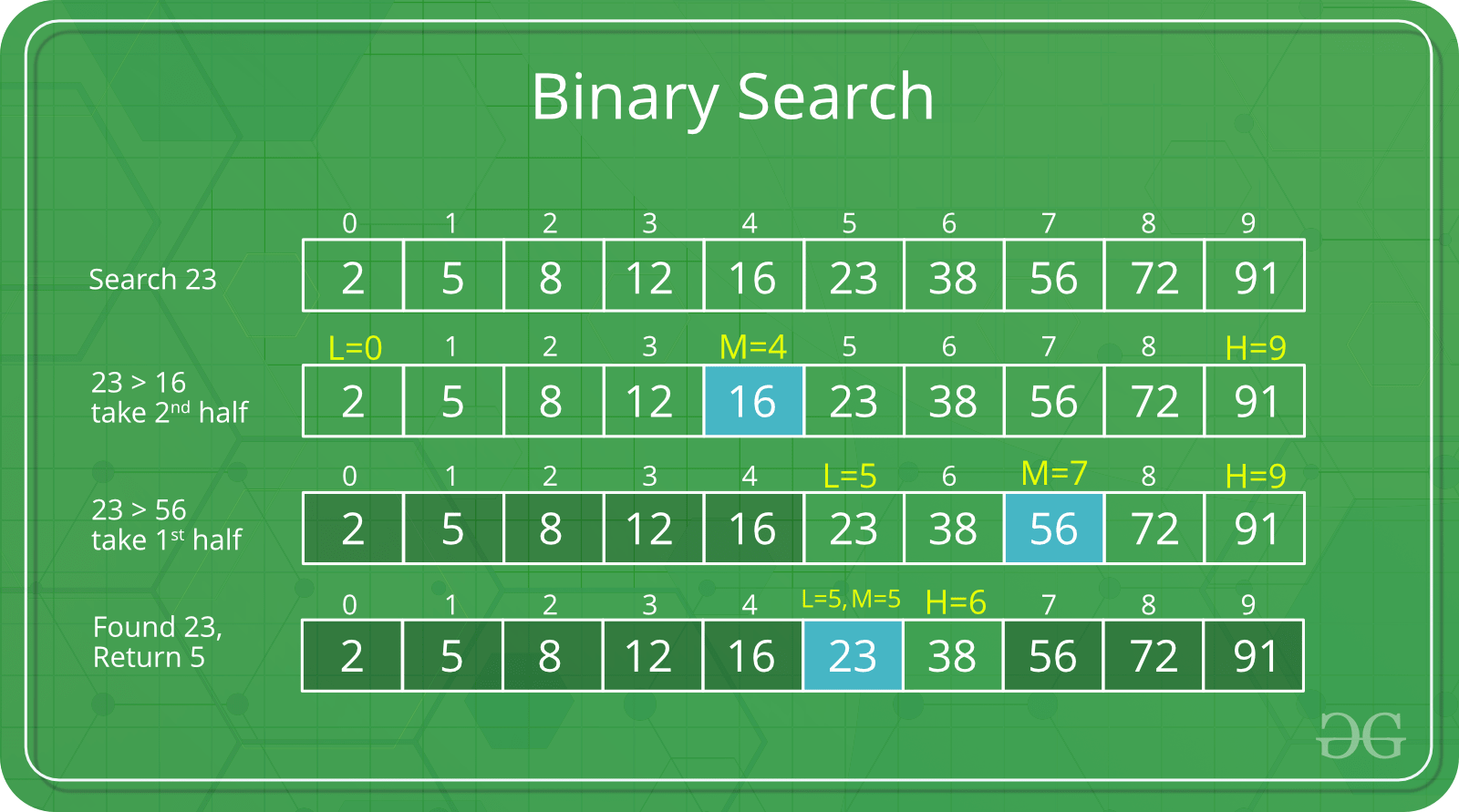
Sorted Array of 10 elements: 2, 5, 8, 12, 16, 23, 38, 56, 72, 91

Let us say we want to search for 23.

Encontrar el elemento dado: 
Ahora, para encontrar 23, habrá muchas iteraciones y cada una tendrá pasos como se menciona en la figura anterior: 

• Iteración 1: 

   

Array: 2, 5, 8, 12, 16, 23, 38, 56, 72, 91

• • Seleccione el elemento del medio. ( aquí 16 )
  • Como 23 es mayor que 16, dividimos el arreglo en dos mitades y consideramos el subarreglo después del elemento 16.
  • Ahora este subarreglo con los elementos después de 16 se tomará en la próxima iteración.
• Iteración 2: 

   

Array: 23, 38, 56, 72, 91

• • Seleccione el elemento del medio. ( ahora 56 )
  • Como 23 es más pequeño que 56, dividimos el arreglo en dos mitades y consideramos el subarreglo antes del elemento 56.
  • Ahora este subarreglo con los elementos anteriores al 56 se tomará en la próxima iteración.
• Iteración 3: 

   

Array: 23, 38

• • Seleccione el elemento del medio. ( ahora 23 )
  • Dado que 23 es el elemento medio. Entonces las iteraciones ahora se detendrán.
  • Digamos que la iteración en Binary Search termina después de k iteraciones. En el ejemplo anterior, termina después de 3 iteraciones, por lo que aquí k = 3
  • En cada iteración, la array se divide por la mitad. Así que digamos que la longitud de la array en cualquier iteración es n
  • En la iteración 1 , 
     

Length of array = n

• En la iteración 2 , 
   

Length of array = n/2

• En la iteración 3 , 
   

Length of array = (n/2)/2 = n/22

• Por lo tanto, después de la iteración k , 
   

Length of array = n/2k

• Además, sabemos que después 
   

After k iterations, the length of array becomes 1

• Por lo tanto , 
   

Length of array = n/2k = 1

=> n = 2k

• Aplicando la función de registro en ambos lados: 
   

=> log2 (n) = log2 (2k)
=> log2 (n) = k log2 2

•  

• Como (log _a (a) = 1) 
  Por lo tanto, 
   

=> k = log2 (n)