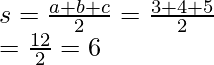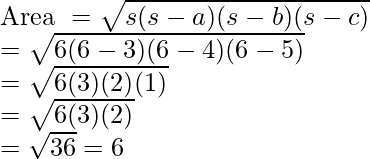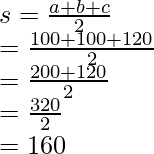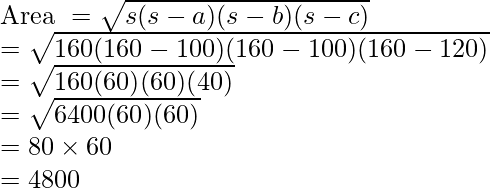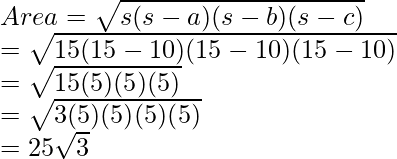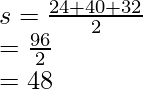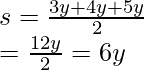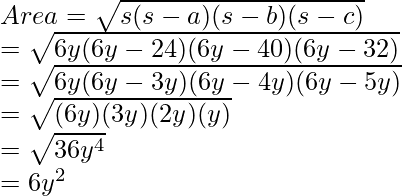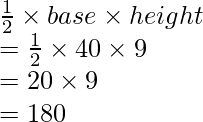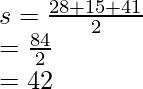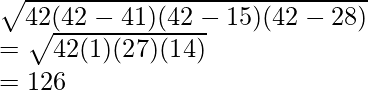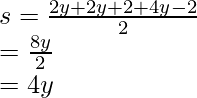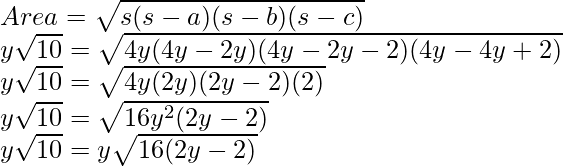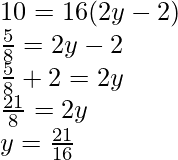Aplicaciones de la fórmula de Heron

Al resolver y encontrar el área de un triángulo, se espera que se proporcionen ciertos parámetros de antemano, por ejemplo, la altura y la base del triángulo deben estar disponibles o, en el caso de un triángulo equilátero, se deben proporcionar las longitudes de los lados.

El área de un triángulo suele estar dada por,

$\frac{1}{2} \times base \times height$

Donde la base y la altura se miden a partir del triángulo dado. Pero a veces puede suceder que no tengamos esa información. Supongamos que solo tenemos información sobre la longitud de los lados. No se sabe la altura, ¿cómo se calculará el área entonces?

La respuesta a esta pregunta es la fórmula de Heron.

Heron nació en Egipto alrededor del año 10AD. Fue un gran matemático, trabajó en matemáticas aplicadas. Su gran cantidad de trabajo giró en torno a cuadrados, rectángulos. Esta fórmula también se llama «Fórmula del héroe».

fórmula de garza

La fórmula de Heron también se conoce como fórmula de Hero, lleva el nombre de un ingeniero muy famoso de Egipto, era famoso y conocido como el «Héroe de Alejandría». Sus obras famosas incluyen la fórmula de Heron, la máquina expendedora, etc. La mejor parte de Heron’s La fórmula era que no requería ningún ángulo o distancia antes de resolver el área de cualquier Triángulo.

Digamos que tenemos un triángulo ABC cuyos lados son de longitud “a”, “b” y “c”.

Entonces el área de ese triángulo dada por Heron,

Area del triangulo ABC $= \sqrt{s(sa)(sb)(sc)}$

Donde a, b y c son la longitud de los lados y s = semiperímetro (La mitad del perímetro)

$s = \frac{a + b + c}{3}$

Esta fórmula nos permite calcular el área del triángulo donde no se da la longitud de la altura.

Aplicación de la fórmula de Heron para encontrar el área de triángulos

La fórmula de Heron se puede usar para encontrar áreas de diferentes tipos de triángulos si se da la longitud de sus lados,

Pregunta: Halla el área del triángulo si sus lados son 3, 5, 4.

Solución:

El área de este triángulo se puede calcular mediante la fórmula de Heron estudiada anteriormente,

Primero calculemos el semiperímetro,

$\\ s = \frac{a + b + c}{2} = \frac{3 + 4 + 5}{2} \\ = \frac{12}{2} = 6$

Introduciendo los valores de s, a, b y c en la fórmula. Calculemos el área.

$\\ \text{Area } = \sqrt{s(s-a)(s-b)(s-c)} \\ = \sqrt{6(6 - 3)(6 - 4)(6 - 5)} \\ = \sqrt{6(3)(2)(1)} \\ = \sqrt{6(3)(2)} \\ = \sqrt{36} = 6$

Por lo tanto, el área del triángulo es de 6 unidades cuadradas.

Aplicación de la fórmula de Heron en la búsqueda del área de cuadriláteros

Sabemos cómo calcular el área de cuadriláteros estándar como rectángulos, cuadrados y trapecios. Pero a veces puede suceder que nuestros cuadriláteros no tengan ninguna de estas formas.

Application of Heron's Formula in Finding Area of Quadrilaterals

El cuadrilátero dado arriba no se encuentra en ninguna de estas categorías, por lo que no se pueden usar nuestras fórmulas estándar. La fórmula de Heron nos ayuda en tales casos. Podemos unir dos vértices opuestos cualquiera en la figura anterior y podemos formar dos triángulos. Entonces se puede calcular el área. Veamos algunos ejemplos al respecto.

Pregunta: Encuentra el área del rombo dado usando la fórmula de Heron.

area of the given rhombus using Heron’s Formula

Solución:

Hay dos triángulos aquí, ambos son similares.

Las longitudes de los lados de ambos triángulos son 100, 100 y 120.

Por lo tanto, el semiperímetro de ambos triángulos es,

$\\ s = \frac{a + b + c}{2} \\ = \frac{100 + 100 + 120}{2} \\ = \frac{200 + 120}{2} \\ = \frac{320}{2} \\ = 160$

ahora calculando el area del triangulo

$\\ \text{Area } = \sqrt{s(s - a)(s - b)(s - c)} \\ = \sqrt{160(160 - 100)(160 - 100)(160 -120)} \\ = \sqrt{160(60)(60)(40)} \\ = \sqrt{6400(60)(60)} \\ = 80 \times 60 \\ = 4800$

Por lo tanto, el área de un solo triángulo es 4800. Ya que hay dos triángulos iguales. Entonces, el área total es de 9600 unidades cuadradas.

Veamos algunos ejemplos de problemas sobre estos conceptos,

Ejemplos de problemas basados en la fórmula de Heron

Pregunta 1: Hay un espacio concreto en forma de triángulo que necesita ser embaldosado. El costo del mosaico es de Rs 20 por unidad cuadrada. Encuentre el costo total de embaldosar el área.

Problem based on Heron’s Formula

Responder:

Las longitudes de los lados dados son 10, 10 y 10.

El semiperímetro “s” = 15

Conocemos el área del triángulo usando la fórmula de Heron.

$\\ Area = \sqrt{s(s - a)(s - b)(s - c)}$

Aquí, s = 15, a = b = c = 10.

$\\ Area = \sqrt{s(s - a)(s - b)(s - c)} \\ = \sqrt{15(15 - 10)(15 - 10)(15 - 10)} \\ = \sqrt{15(5)(5)(5)} \\ = \sqrt{3(5)(5)(5)(5)} \\ = 25\sqrt{3}$

El área del triángulo es 25√3

Entonces, el costo de teselar el área = 25√3 x 20

= 500√3

= 500 (1,73)

= 866 (aprox.)

Por lo tanto, el costo de embaldosar el área es de Rs. 866.

Pregunta 2: La longitud de los lados de un triángulo está en una proporción de 3:5:4 y el perímetro es de 96 m. Encuentra el área del triángulo.

Solución:

Los lados están en proporción de 3:5:4. Supongamos que la longitud de los lados es 3x, 5x y 4x.

3x + 5x + 4x = 96

= 12x = 96

= x = 8.

Por lo tanto, los lados son 24, 40, 32. Ahora calculemos «s» e introduzcamos los valores en la fórmula de Heron.

$\\ s = \frac{24 + 40 + 32}{2} \\ = \frac{96}{2} \\ = 48$

$\\ Area = \sqrt{s(s - a)(s - b)(s - c)} \\ = \sqrt{48(48 - 24)(48 - 40)(48 - 32)} \\ = \sqrt{48(24)(8)(16)} \\ = \sqrt{(24)(2)(24)(8)(16)} \\ = \sqrt{(24^2)(16^2)}\\ = 24 \times 16 = 384$

Pregunta 3: Digamos que los lados del triángulo se dan como 3y, 4y y 5y. Halla la expresión del área del triángulo.

Responder:

Averigüemos el perímetro y el semiperímetro para que podamos reemplazar los valores en la fórmula de Heron.

$\\ s = \frac{3y + 4y + 5y}{2}\\ = \frac{12y}{2} = 6y$

Introduciendo los valores en la fórmula de Heron.

$\\ Area = \sqrt{s(s - a)(s - b)(s - c)} \\ = \sqrt{6y(6y - 24)(6y - 40)(6y - 32)} \\ = \sqrt{6y(6y - 3y)(6y - 4y)(6y - 5y)} \\ = \sqrt{(6y)(3y)(2y)(y)} \\ = \sqrt{36y^4}\\ = 6y^2$

Pregunta 4: Encuentra el área del cuadrilátero dado a continuación:

Problem based on Heron’s Formula

Solución:

El cuadrilátero ABCD se puede dividir en dos triángulos cuya área podemos calcular si unimos A y C.

Ahora tenemos los triángulos ACD y ABC. De los cuales ACD es un triángulo rectángulo.

CA ² = AD ² + CC ²

⇒ CA ² = 9 ² + 40 ²

⇒ CA ² = 81 + 1600

⇒ CA ² = 1681

⇒ CA = 41

Área del triángulo ADC = $\\ \frac{1}{2} \times base \times height \\ = \frac{1}{2} \times 40 \times 9 \\ = 20 \times 9 \\ = 180$

El área del triángulo ABC se calculará usando la fórmula de Heron. Los lados del triángulo son 28,15 y 41.

$\\ s = \frac{28 + 15 + 41}{2} \\ = \frac{84}{2} \\ = 42$

Área del triángulo ABC = $\\ \sqrt{42(42 - 41)(42 - 15)(42 - 28)} \\ = \sqrt{42(1)(27)(14)} \\ = 126$

Área del cuadrilátero = Área del triángulo ADC+ Área del triángulo ABC

= 180 + 126

= 306 unidades cuadradas.

Pregunta 5: Supongamos un triángulo cuyos lados son 2y, 2y + 2 y 4y – 2 y su área es y√10. Halla el valor de y.

Solución:

Calculemos «s»

$\\ s = \frac{2y + 2y + 2 + 4y - 2}{2} \\ = \frac{8y}{2} \\ = 4y$

$\\ Area = \sqrt{s(s - a)(s - b)(s - c)} \\ y\sqrt{10} = \sqrt{4y(4y - 2y)(4y - 2y - 2)(4y - 4y + 2)}\\ y\sqrt{10} = \sqrt{4y(2y)(2y - 2)(2)} \\ y\sqrt{10} = \sqrt{16y^2(2y - 2)} \\ y\sqrt{10} = y\sqrt{16(2y - 2)} \\$

Comparando ambos lados de la ecuación,

$\\ 10 = 16(2y - 2) \\ \frac{5}{8} = 2y - 2 \\ \frac{5}{8} + 2 = 2y \\ \frac{21}{8} = 2y \\ y = \frac{21}{16}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

fórmula de garza

Aplicación de la fórmula de Heron para encontrar el área de triángulos

Aplicación de la fórmula de Heron en la búsqueda del área de cuadriláteros

Ejemplos de problemas basados ​​en la fórmula de Heron

Deja una respuesta Cancelar la respuesta

Ejemplos de problemas basados en la fórmula de Heron