Área del triángulo formado por los ejes de coordenadas y una recta dada

Dada una línea recta con coeficientes de ecuación como a , b y c (ax + by + c = 0), la tarea es encontrar el área del triángulo formado por los ejes de coordenadas y esta línea recta.
Ejemplos: 
 

Input: a = -2, b = 4, c = 3
Output: 0.5625

Input: a = 4, b = 3, c = 12
Output: 6

Enfoque : 
 

1. Sea PQ la recta que tiene AB , el segmento de recta entre los ejes. 
   La ecuación es, 
   ax + by + c = 0 
    
2. entonces, en forma de intersección se puede expresar como, 
   x/(-c/a) + y/(-c/b) = 1 
    
3. Entonces, la intersección x = -c/a 
   la intersección y = -c/b 
    
4. Entonces, está muy claro ahora que la base del triángulo AOB será -c/a 
   y la base del triángulo AOB será -c/b 
    
5. Entonces, el área del triángulo 
   
    

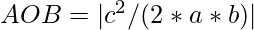
A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program area of triangle
// formed by the axes of co-ordinates
// and a given straight line
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find area
double area(double a, double b, double c)
{
    double d = fabs((c * c) / (2 * a * b));
    return d;
}
 
// Driver code
int main()
{
    double a = -2, b = 4, c = 3;
    cout << area(a, b, c);
    return 0;
}

// Java program area of triangle
// formed by the axes of co-ordinates
// and a given straight line
 
import java.io.*;
 
class GFG
{
 
// Function to find area
static double area(double a, double b, double c)
{
    double d = Math.abs((c * c) / (2 * a * b));
    return d;
}
 
// Driver code
public static void main (String[] args)
{
     
    double a = -2, b = 4, c = 3;
    System.out.println(area(a, b, c));
}
}
 
// This code is contributed by ajit.

# Python3 program area of triangle
# formed by the axes of co-ordinates
# and a given straight line
 
# Function to find area
def area(a, b, c):
 
    d = abs((c * c) / (2 * a * b))
    return d
 
# Driver code
a = -2
b = 4
c = 3
print(area(a, b, c))
 
# This code is contributed
# by mohit kumar

// C# program area of triangle
// formed by the axes of co-ordinates
// and a given straight line
using System;
 
class GFG
{
     
// Function to find area
static double area(double a, double b, double c)
{
    double d = Math.Abs((c * c) / (2 * a * b));
    return d;
}
 
// Driver code
static public void Main ()
{
     
    double a = -2, b = 4, c = 3;
    Console.WriteLine (area(a, b, c));
}
}
 
// This code is contributed by akt_mit.

<?php
// PHP program area of triangle
// formed by the axes of co-ordinates
// and a given straight line
 
// Function to find area
function area($a, $b, $c)
{
    $d = abs(($c * $c) / (2 * $a * $b));
    return $d;
}
 
// Driver code
$a = -2;
$b = 4;
$c = 3;
 
echo area($a, $b, $c);
 
// This code is contributed by Ryuga
?>

<script>
 
// javascript program area of triangle
// formed by the axes of co-ordinates
// and a given straight line
 
// Function to find area
function area(a , b , c)
{
    var d = Math.abs((c * c) / (2 * a * b));
    return d;
}
 
// Driver code
     
var a = -2, b = 4, c = 3;
document.write(area(a, b, c));
 
 
// This code is contributed by Amit Katiyar
 
</script>

0.5625

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)