Área de un triángulo con dos vértices en los puntos medios de los lados opuestos de un cuadrado y el otro vértice sobre el vértice de un cuadrado

Dado un entero positivo N que representa el lado de un cuadrado, la tarea es encontrar el área de un triángulo formado al conectar los puntos medios de dos lados adyacentes y el vértice opuesto a los dos lados.

Ejemplos:

Entrada: N = 10
Salida: 37,5

Entrada: N = 1
Salida: 0,375

Enfoque: El problema dado se puede resolver con base en las siguientes observaciones:

• El lado uno del triángulo será la hipotenusa del triángulo formado con los vértices como dos puntos medios y un vértice del cuadrado en la intersección de los lados cuya longitud del lado está dada por  .
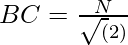• La longitud de los otros dos lados del triángulo está dada por  .
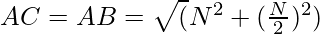• Ahora, los lados del triángulo se conocen, por lo tanto, el área del triángulo se puede calcular usando la fórmula de Heron .

Siga los pasos a continuación para resolver el problema:

• Encuentre el lado del triángulo como se discutió anteriormente en la fórmula y guárdelo en las variables, digamos a , b y c , respectivamente.
• Después de completar los pasos anteriores, imprima el valor de (s*(s – a)*(s – b)*(s – c)) ^1/2 donde s = (a + b + c) / 2 .

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the area of the
// triangle that inscribed in square
double areaOftriangle(int side)
{
    // Stores the length of the first
    // side of triangle
    double a = sqrt(pow(side / 2, 2)
                    + pow(side / 2, 2));
 
    // Stores the length of the second
    // side of triangle
    double b = sqrt(pow(side, 2)
                    + pow(side / 2, 2));
 
    // Stores the length of the third
    // side of triangle
    double c = sqrt(pow(side, 2)
                    + pow(side / 2, 2));
 
    double s = (a + b + c) / 2;
 
    // Stores the area of the triangle
    double area = sqrt(s * (s - a)
                       * (s - b) * (s - c));
 
    // Return the resultant area
    return area;
}
 
// Driver Code
int main()
{
    int N = 10;
    cout << areaOftriangle(N);
 
    return 0;
}

// Java program for the above approach
import java.util.*;
 
class GFG{
  
// Function to find the area of the
// triangle that inscribed in square
static double areaOftriangle(int side)
{
     
    // Stores the length of the first
    // side of triangle
    double a = Math.sqrt(Math.pow(side / 2, 2) +
                         Math.pow(side / 2, 2));
 
    // Stores the length of the second
    // side of triangle
    double b = Math.sqrt(Math.pow(side, 2) +
                         Math.pow(side / 2, 2));
 
    // Stores the length of the third
    // side of triangle
    double c = Math.sqrt(Math.pow(side, 2) +
                         Math.pow(side / 2, 2));
 
    double s = (a + b + c) / 2;
 
    // Stores the area of the triangle
    double area = Math.sqrt(s * (s - a) *
                           (s - b) * (s - c));
 
    // Return the resultant area
    return area;
}
  
// Driver code
public static void main(String[] args)
{
    int N = 10;
     
    System.out.print(areaOftriangle(N));
}
}
 
// This code is contributed by sanjoy_62

# Python3 program for the above approach
from math import sqrt
 
# Function to find the area of the
# triangle that inscribed in square
def areaOftriangle(side):
     
    # Stores the length of the first
    # side of triangle
    a = sqrt(pow(side / 2, 2) + pow(side / 2, 2))
 
    # Stores the length of the second
    # side of triangle
    b = sqrt(pow(side, 2) + pow(side / 2, 2))
 
    # Stores the length of the third
    # side of triangle
    c = sqrt(pow(side, 2) + pow(side / 2, 2))
 
    s = (a + b + c) / 2
 
    # Stores the area of the triangle
    area = sqrt(s * (s - a) * (s - b) * (s - c))
 
    # Return the resultant area
    return round(area, 1)
 
# Driver Code
if __name__ == '__main__':
     
    N = 10
     
    print (areaOftriangle(N))
 
# This code is contributed by mohit kumar 29

// C# program for the above approach
using System;
class GFG{
  
// Function to find the area of the
// triangle that inscribed in square
static double areaOftriangle(int side)
{
     
    // Stores the length of the first
    // side of triangle
    double a = Math.Sqrt(Math.Pow(side / 2, 2) +
                         Math.Pow(side / 2, 2));
 
    // Stores the length of the second
    // side of triangle
    double b = Math.Sqrt(Math.Pow(side, 2) +
                         Math.Pow(side / 2, 2));
 
    // Stores the length of the third
    // side of triangle
    double c = Math.Sqrt(Math.Pow(side, 2) +
                         Math.Pow(side / 2, 2));
 
    double s = (a + b + c) / 2;
 
    // Stores the area of the triangle
    double area = Math.Sqrt(s * (s - a) *
                           (s - b) * (s - c));
 
    // Return the resultant area
    return area;
}
  
// Driver code
public static void Main(string[] args)
{
    int N = 10;
     
    Console.WriteLine(areaOftriangle(N));
}}
 
// This code is contributed by ukasp.

<script>
    // Javascript program for the above approach
     
    // Function to find the area of the
    // triangle that inscribed in square
    function areaOftriangle(side)
    {
 
        // Stores the length of the first
        // side of triangle
        let a = Math.sqrt(Math.pow(side / 2, 2) +
                             Math.pow(side / 2, 2));
 
        // Stores the length of the second
        // side of triangle
        let b = Math.sqrt(Math.pow(side, 2) +
                             Math.pow(side / 2, 2));
 
        // Stores the length of the third
        // side of triangle
        let c = Math.sqrt(Math.pow(side, 2) +
                             Math.pow(side / 2, 2));
 
        let s = (a + b + c) / 2;
 
        // Stores the area of the triangle
        let area = Math.sqrt(s * (s - a) *
                               (s - b) * (s - c));
 
        // Return the resultant area
        return area.toFixed(1);
    }
     
    let N = 10;
      
    document.write(areaOftriangle(N));
 
// This code is contributed by suresh07.
</script>

37.5

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)