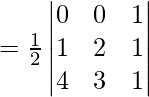Área de un Triángulo usando Determinantes | Clase 12 Matemáticas

Anteriormente hemos aprendido que el determinante es el valor escalar que se calcula a partir de diferentes elementos de la array cuadrada que tiene ciertas propiedades de una transformación lineal. Ahora aprendamos a usar los determinantes para encontrar el área del triángulo, digamos que (x1, y1), (x2, y2), (x3, y3) son los 3 puntos del triángulo en el plano cartesiano ahora el el area del triangulo sera dada como

fórmula para el área del triángulo

$\alpha = \frac{1}{2}\left [ x_{1}(y_{2}-y_{3})+ x_{2}(y_{3}-y_{1}) + x_{3}(y_{1}-y_{2})\right]$

dónde,

∝ = Área del Triángulo

x1, y1, x2, y2, x3 e y3 = vértices del triángulo

La fórmula para ubicar el área se puede representar dentro del tipo de determinantes que se indican a continuación:

$\alpha = \frac{1}{2}\begin{vmatrix} x_{1} &y_{1} &1 \\ x_{2} &y_{2} & 1\\ x_{3} &y_{3} &1 \end{vmatrix}$

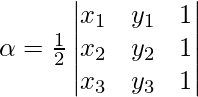
Como todos sabemos, el valor de un determinante puede ser negativo o un valor positivo, pero como estamos hablando de un área y nunca puede tomarse como un valor negativo, tomamos absolutamente el valor del determinante así obtenido.

Si el mundo de Triangulum ya está dado, entonces hacemos uso de los valores positivos y negativos del determinante.

Además, si tres puntos son colineales, podríamos quedarnos con una línea en lugar de un triángulo y debido a que el área encerrada por una línea es cero, el valor del determinante también será cero.

Teniendo en cuenta los puntos mencionados anteriormente, permítanos intentar expandir el determinante que denota el mundo usando técnicas de expansión de determinantes usando menores y cofactores.

Problemas basados en el área de un triángulo

Problema 1: Encuentra el área del triángulo cuyos vértices son (0, 0), (1, 2) y (4, 3).

Solución:

Sea el punto (x1, y1) ==> (0, 0), (x2, y2) ==> (1, 2) y (x3, y3) ==> (4, 3)

$= \frac{1}{2}\begin{vmatrix} 0 &0 &1 \\ 1 &2 & 1\\ 4 &3 &1 \end{vmatrix}$

= (1/2)[3 – 8]

= (1/2)[-5]

= -5/2

= -2.5

El área no se puede representar con negativo. Por lo tanto, el área del triángulo con vértices dados es de 2,5 unidades cuadradas.

Problema 2: Si (k, 2), (2, 4) y (3, 2) son vértices del triángulo de área 4 unidades cuadradas entonces determina el valor de k.

Solución:

Área del triángulo = 4 unidades cuadradas

$= \frac{1}{2}\begin{vmatrix} k &2 &1 \\ 2 &4 & 1\\ 3 &2 &1 \end{vmatrix}$

(1/2){k [4 – 2] – 2[2 – 3] + 1[4 – 12]} = 4

k(2) – 2(-1) + 1(-8) = 8

2k + 2 – 8 = 8

2k – 6 = 8

2k = 8 + 6

2k = 14

k = 7

Entonces, el valor de k es 7.

Problema 3: Los vértices de un triángulo son (-2, -3), (3, 2) y (-1, -8). hallar el area del triangulo??

Solución:

$= \frac{1}{2}\begin{vmatrix} -2 &-3 &1 \\ 3 &2 & 1\\ -1 &-8 &1 \end{vmatrix}$

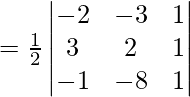
= (1/2) [ -2(2 + 8) + 3(3+1) + 1(-24 + 2) ]

= (1/2) [-2 (10) + 3(4) + 1(-22)]

= (1/2) [ -20 + 12 – 22]

= (1/2) [-42 + 12]

= (1/2) (-30)

= -15

Entonces, el área requerida es de 15 unidades cuadradas.

Publicación traducida automáticamente

Artículo escrito por pulkitagarwal03pulkit y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

fórmula para el área del triángulo

Problemas basados ​​en el área de un triángulo

Deja una respuesta Cancelar la respuesta

Problemas basados en el área de un triángulo