Calcular la razón del área de un triángulo inscrito en una Elipse y el triángulo formado por los puntos correspondientes en el círculo auxiliar

Dados dos números enteros A y B que representan las longitudes de los ejes semi-mayor y semi-menor de una elipse , la tarea es calcular la relación de cualquier triángulo inscrito en la elipse y la del triángulo formado por los puntos correspondientes en su círculo auxiliar .

Ejemplos:

Entrada : A = 1, B = 2
Salida : 2
Explicación : Relación = B / A = 2 / 1 = 2

Entrada : A = 2, B = 3
Salida : 1,5

Acercarse:

La idea se basa en la siguiente fórmula matemática:

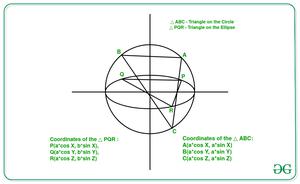
• Sean los 3 puntos de la elipse P(a cosX, b senX), Q(a cosY, b senY), R(a cosZ, b senZ).
• Por lo tanto, los puntos correspondientes en los círculos auxiliares son A(a cosX, a senX), B(a cosY, a senY), C(a cosZ, a senZ). 
• Ahora, usando la fórmula para calcular el área del triángulo usando los puntos dados del triángulo.

Área (PQR) / Área (ABC) = b / a

Siga los pasos a continuación para resolver el problema:

• Almacene la relación entre el semieje mayor y el semieje menor de la elipse en una variable, digamos resultado.
• Imprime el valor del resultado como la respuesta requerida. 

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to calculate ratio of a
// triangle inscribed in an ellipse to
// the triangle on the auxiliary circle
void triangleArea(int a, int b)
{
    // Stores the ratio of the
    // semi-major to semi-minor axes
    double ratio = (double)b / a;
 
    // Print the ratio
    cout << ratio;
}
 
// Driver Code
int main()
{
    int a = 1, b = 2;
    triangleArea(a, b);
 
    return 0;
}

// Java program for the above approach
class GFG{
  
// Function to calculate ratio of a
// triangle inscribed in an ellipse to
// the triangle on the auxiliary circle
static void triangleArea(int a, int b)
{
     
    // Stores the ratio of the
    // semi-major to semi-minor axes
    double ratio = (double)b / a;
 
    // Print the ratio
    System.out.println(ratio);
}
 
// Driver Code
public static void main(String args[])
{
    int a = 1, b = 2;
     
    triangleArea(a, b);
}
}
 
// This code is contributed by AnkThon

# Python3 program for the above approach
 
# Function to calculate ratio of a
# triangle inscribed in an ellipse to
# the triangle on the auxiliary circle
def triangleArea(a, b):
 
    # Stores the ratio of the
    # semi-major to semi-minor axes
    ratio = b / a
 
    # Print the ratio
    print(ratio)
 
# Driver Code
if __name__ == "__main__" :
 
    a = 1
    b = 2
     
    triangleArea(a, b)
 
# This code is contributed by AnkThon

// C# program for the above approach
using System;
using System.Collections.Generic;
 
class GFG{
  
// Function to calculate ratio of a
// triangle inscribed in an ellipse to
// the triangle on the auxiliary circle
static void triangleArea(int a, int b)
{
     
    // Stores the ratio of the
    // semi-major to semi-minor axes
    double ratio = (double)b / a;
 
    // Print the ratio
    Console.WriteLine(ratio);
}
 
// Driver Code
public static void Main()
{
    int a = 1, b = 2;
     
    triangleArea(a, b);
}
}
 
// This code is contributed by bgangwar59

<script>
 
// JavaScript program for the above approach
 
// Function to calculate ratio of a
// triangle inscribed in an ellipse to
// the triangle on the auxiliary circle
function triangleArea(a, b){
 
    // Stores the ratio of the
    // semi-major to semi-minor axes
    ratio = b / a
 
    // Print the ratio
    document.write(ratio)
}
 
// Driver Code
var a = 1
var b = 2
     
triangleArea(a, b)
 
// This code is contributed by AnkThon
 
</script>

2

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)