Clase 12 Soluciones NCERT – Matemáticas Parte I – Aplicación de Derivadas – Ejercicio 6.1

Pregunta 1. Encuentra la tasa de cambio del área de un círculo con respecto a su radio r cuando a) r=3cm b) r=4cm

Solución:

Dado,

radio del circulo=r=3cm

Ahora sabemos que area= πr ² =A

Tasa de cambio del área de un círculo con respecto a r=dA/dr

dA/dr=d/dr πr ² =2πr

entonces, cuando r=3

dA/dr

=2π(3)=6π

cuando r=4

dA/dr

=2π(4)=8π

Pregunta 2. El volumen de un cubo aumenta a razón de cm ³ /s. ¿Qué tan rápido aumenta el área de la superficie cuando la longitud de un borde es de 12 cm?

Solución:

Dado,

Tasa de aumento del volumen =8cm ³ /s

longitud de la arista del cubo = 12 cm = s

Ahora,

volumen (v) de un cubo con longitud de lado ‘s’

v = s ³

Ahora, $\frac{dv}{dt}=\frac{d(s)^3}{dt}=3s^2\frac{ds}{dt}$ [regla de la string]

$\frac{dv}{dt}=8cm^3/s=3(12)^2\frac{ds}{dt}$

$\frac{ds}{dt}=\frac{8cm^3}{3(12)^2cm^2}$

entonces, la tasa de cambio del área de superficie (A)

A=6s ²

$\frac{dA}{dt}=\frac{d}{dt}(6s^2)=36(2s)\frac{ds}{dt}$

$\frac{dA}{dt}=12.12.\frac{ds}{dt}=\frac{8}{3}cm^2/s$

Pregunta 3. El radio de un círculo aumenta uniformemente a razón de 3 cm/s. Encuentre la tasa a la que aumenta el área del círculo cuando el radio es de 10 cm.

Solución:

Dado,

tasa de aumento del radio = 3cm/s=r

Entonces, $\frac{dr}{dt}$ = 3cm\s

Para encontrar: Razón de aumento del Área ( A = πr ²)

$\frac{dA}{dt}$ = π $\frac{d}{dt}(r^2)$ =2πr. $\frac{dr}{dt}$ [string de reglas]

$\frac{dA}{dt}$ =2π(10) ³ =60πr

Pregunta 4. La arista de un cubo variable crece a razón de 3 cm/s. ¿Qué tan rápido aumenta el volumen del cubo cuando la arista mide 10 cm de largo?

Solución:

Dado: tasa de aumento de la arista del cubo, $\frac{ds}{dt}$ =3cm/s

Hallar: Tasa de aumento de volumen (v) del cubo $\frac{dv}{dt}=?$

Ahora, $\frac{dv}{dt}=\frac{d}{dt}(s^3)=3s^2.\frac{ds}{dt}$ [regla de la string]

Asi que, $\frac{dv}{dt}=3(10)^2.3cm^3/s=900cm^3/s$

Pregunta 5. Se deja caer una piedra en un lago tranquilo y las ondas se mueven en círculos a una velocidad de 5 cm/s. En el instante en que el radio de la onda circular es de 8 cm, ¿con qué rapidez aumenta el área encerrada?

Solución:

Dado, Velocidad del agua = tasa de cambio de radio = 5 cm/s

Para encontrar: tasa de aumento del área = $\frac{dA}{dt}=?$

$\frac{dr}{dt}=5cm/s$

$\frac{dA}{dt}$ = π $\frac{d}{dt}(r^2)$ =2πr. $\frac{dr}{dt}$ [string de reglas]

$\frac{dA}{dt}$ = 2π(8)5cm ² /s

⁼ 80πcm2 /s

Pregunta 6. El radio de un círculo aumenta a razón de 0,7 cm/s. ¿Cuál es la tasa de aumento de sus circunstancias?

Solución:

Dado: tasa de aumento del radio, $\frac{dr}{dt}=0.7cm/s$

Circunferencia(P)=2 πr

$\frac{dP}{dt}$ =2π. $\frac{dr}{dt}$ =2π.(0.7)

$\frac{dP}{dt}$ =1.4π cm/s o 4.4cm/s [tomando π=22/7]

Pregunta 7. La longitud x de un rectángulo disminuye a razón de 5 cm/minuto y el ancho y aumenta a razón de 4 cm/minuto. Cuando x = 8 cm y y = 6 cm, encuentre las tasas de cambio de (a) el perímetro yb) el área del rectángulo.

Solución:

Dado: Tasa de cambio de longitud, $\frac{dx}{dt}=-5cm/min$

Tasa de cambio de ancho, $\frac{dy}{dt}=4cm/min$

Ahora, perímetro P=2(r+y)

Área A=xy

entonces, a) $\frac{dP}{dt}=\frac{d}{dt}(2(x+Y))=\frac{2dx}{dt}+\frac{2dy}{dt}$

$\frac{dP}{dt}=2.(-5)+2.(4)=-2cm/min$

b) $\frac{dA}{dt}=\frac{d}{dx}(x.y)=x\frac{dy}{dt}+y\frac{dx}{dt}$ [x es decreciente, y es creciente]

$\frac{dA}{dt}=8(4)+6(-5)=2cm/min$

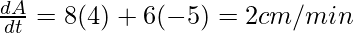
Pregunta 8. Un globo, que siempre permanece esférico al inflarse, se infla bombeando 900 centímetros cúbicos de gas por segundo. Encuentre la tasa a la que aumenta el radio del globo cuando el radio es de 15 cm.

Solución:

Dado, Cantidad de gas bombeado por segundo/ Tasa de cambio de volumen $\frac{dv}{dt}$ = 900 cm ³ /s

Para encontrar: Tasa de cambio del radio, $\frac{dr}{dt}$ cuando r=15cm.

v= $\frac{4}{3}$ πr ³

$\frac{dv}{dt}$ = 4πr ² $\frac{dr}{dt}$

Ahora, $\frac{dv}{dt}$ =4π(15) ² . $\frac{dr}{dt}$

900=900π. $\frac{dr}{dt}$

$\frac{dr}{dt}$ = 1/πcm/s

Pregunta 9. Un globo, en el que siempre permanece esférico, tiene un radio variable. Encuentre la tasa a la que su volumen aumenta con el radio cuando el último es de 10 cm.

Solución:

Sea el radio r y el volumen v.

v= $\frac{4}{3}$ πr ³

Hallar: Tasa de cambio de volumen con respecto a

es decir $\frac{dv}{dr}=?$

Ahora, $\frac{dv}{dt}=\frac{4}{3}$ π $\frac{d}{dr}$ .r ³ =4πr ²

$\frac{dv}{dr}$ ⁼ 400πcm2

Pregunta 10. Una escalera de 5 m de largo está apoyada contra una pared. La parte inferior de la escalera se tira por el suelo, alejándola de la pared, a razón de 2 cm/s. ¿Qué tan rápido disminuye su altura sobre la pared cuando el pie de la escalera está a 4 m de la pared?

Solución:

Dado: Longitud de las escaleras = 5m

En ∆ ABC, AC=5m, BC=4m, & ∠ABC=90°,

Entonces, por el teorema de Pitágoras,

AB= $\sqrt{(5)^2-(4)^2}$ =3

Ahora, sea AB=x & BC=y

entonces, x ² ,y ² =5 ² o x ² ,y ² =25 ———1

Derivando ambos lados de 1 por t, obtenemos

$2x.\frac{dx}{dt}+2y.\frac{dy}{dt}=0$

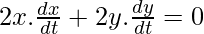
o

$x.\frac{dx}{dt}=-y.\frac{dy}{dt}$

Ahora en BC=y=4,

$\frac{dy}{dt}=2cm/s$

asi que $x.\frac{dx}{dt}=-y\frac{dy}{dt}$

$3\frac{dx}{dt}=-4(2)$

$\frac{dx}{dt}=\frac{-8}{3}cm/s$ [el signo negativo significa que AB está disminuyendo]

Pregunta 11. Una partícula se mueve a lo largo de la curva 6y=x ³ + 2. Encuentra los puntos en la curva en los que la coordenada y cambia 8 veces más rápido que la coordenada x.

Solución:

Dado: curva 6y=x ³ +2 ————1

y $\frac{dy}{dt}=8.\frac{dx}{dt}$ ———-2

Diferencialmente 1 con respecto a él, obtenemos,

$\frac{6dy}{dt}=3x^2.\frac{dx}{dt}$

de 2 6.8. $\frac{dx}{dt}=3x^2.\frac{dx}{dt}$

¹⁶ =x2

x=±4 ————-3

Ahora para las coordenadas y, pon 3

6y=x ³ +2

cuando x = -4

6y = -64+2

y = $\frac{32}{3}$

y, cuando x = 4

6 años = 66

y = 11

Pregunta 12. El radio de una burbuja de aire aumenta a razón de 1/2 cm/s. ¿A qué tasa aumenta el volumen de la burbuja cuando el radio es de 1 cm?

Solución:

Dado: Tasa de incremento del radio $\frac{dr}{dt}=\frac{1}{2}$ cm/s

Para encontrar: tasa de aumento de volumen, $\frac{dv}{dt}=?$

Ahora, v=4/3 πr ³

$\frac{dv}{dt}$ = $\frac{4}{3}$ π $\frac{d}{dt}(r^3)$ =4πr ² $\frac{dr}{dt}$
$\frac{dv}{dt}$ =4π(1) ² . $\frac{1}{2}$ cm ³ /s

$\frac{dv}{dt}$ =2π cm ³ /s

Pregunta 13. Un globo, que siempre permanece esférico, tiene un diámetro variable 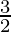$\frac{3}{2}$ (2x+1). Encuentre la tasa de cambio de su volumen con respecto a x.

Solución:

Dado: Diámetro de la esfera=3/2(2x+1)=d

Entonces, el radio de la esfera será d/2=3/4(2x+1)=r

$\frac{dr}{dx} = \frac{3}{4}$ (2)

$\frac{dr}{dx} = \frac{3}{2}$

Ahora, volumen =4/3 πr ³

Tasa de cambio de volumen con respecto al radio

$\frac{dv}{dr}$ = $\frac{4}{3}$ π $\frac{d}{dr}(r^3)$ =4πr ²

$\frac{dv}{dr} . \frac{dr}{dx}$ = 4π( $(\frac{3(2x+1)}{4})^2 . \frac{3}{2}$

$\frac{dv}{dx} = \frac{27}{8}$ π (2x+1) ²

Pregunta 14. Sale arena de un tubo a razón de 12 cm ³ /s. La arena que cae forma un cono en el suelo de tal manera que la altura del cono es siempre un sexto del radio de la base. ¿Qué tan rápido aumenta la altura del cono cuando la altura es de 4 cm?

Solución:

Dado: Tasa de caída de arena=12cm ³ /s

Ahora bien, esta tasa es básicamente la tasa de cambio del cono.

asi que, $\frac{dv}{dt}=12cm^3/s$

Ahora, radio =r

altura =r

la altura es siempre un sexto del radio, entonces,

h=r/6 o r=6h

Para encontrar: Tasa de cambio de altura =dh/dt=?

Ahora, volumen v=1/3 πr ² h=1/3.π(6h) ² .h

v=12πh ³

$\frac{dv}{dt}$ =12π $\frac{d}{dt}(h^3)$ =12π3h ² . $\frac{dh}{dt}$

12 =36π.(4)2. $\frac{dh}{dt}$

$\frac{12}{36.16}$ = π $\frac{dh}{dt}$

$\frac{dh}{dt}$ =1 / 48πcm/s

Pregunta 15. El costo total C(x) en rupias asociado con la producción de x unidades de un artículo está dado por C(x)=0.003x ² +15x+4000. Encuentre el costo marginal cuando se producen 17 unidades.

Solución:

Dado: c(x)=0.007x ³ -0.003x ² +15c+4000

Ahora, el cambio en el costo total con respecto a las unidades se conoce como costo marginal, es decir $\frac{dc(x)}{dx}$

$\frac{d[(x)]}{dx}=\frac{d}{dx}(0.007x^3-0.003x^2+15x+4000)$

Coste marginal=0,021x ² -0,006x+15

Costo marginal cuando se producen 17 unidades

=0.221(17) ² -0.006(17)+15

=6.069-0.102+15

=20.967

Pregunta 16. El ingreso total en rupias de la escala de x unidades de un producto viene dado por R(x)=13x ³ +26x+15. Encuentre el ingreso marginal cuando x=7.

Solución:

El ingreso marginal es la tasa de cambio del ingreso total con respecto al no. de unidades.

Entonces, ingreso marginal = $\frac{d}{dx}[R(x)]$

Ingreso marginal = $\frac{d}{dx}(13x^2+26x+15)$

$=26x+26=26(x+1)$

Ingreso marginal cuando (x=7)

=26 (8)

=208

Pregunta 17. La tasa de cambio del área del círculo con respecto a su radio r en r= 6cm es (A) 10π (B) 12π (C) 8π (D) 11π.

Solución:

Área, A=πr ² ,donde r es el radio

La tasa de cambio de área con respecto a su radio r es,

$\frac{dA}{dr}$ =π $\frac{d}{dr}(r^2)$ =2πr

$\frac{dA}{dr}$ =2π(6)=12π

Pregunta 18. El ingreso total en rupias recibido por la venta de x unidades de un producto viene dado por R(x)=3x ² +36x+5. El ingreso marginal, cuando x=15 es (A) 116 (B) 96 (C) 90 (D) 126

Solución:

Ingreso Marginal= $\frac{d}{dx}(R(x))$

Ingresos marginales = 6x + 36

El ingreso marginal en x=15 es 6 (15)+36=126

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la tasa de cambio del área de un círculo con respecto a su radio r cuando a) r=3cm b) r=4cm

Pregunta 2. El volumen de un cubo aumenta a razón de cm 3 /s. ¿Qué tan rápido aumenta el área de la superficie cuando la longitud de un borde es de 12 cm?

Pregunta 3. El radio de un círculo aumenta uniformemente a razón de 3 cm/s. Encuentre la tasa a la que aumenta el área del círculo cuando el radio es de 10 cm.

Pregunta 4. La arista de un cubo variable crece a razón de 3 cm/s. ¿Qué tan rápido aumenta el volumen del cubo cuando la arista mide 10 cm de largo?

Pregunta 5. Se deja caer una piedra en un lago tranquilo y las ondas se mueven en círculos a una velocidad de 5 cm/s. En el instante en que el radio de la onda circular es de 8 cm, ¿con qué rapidez aumenta el área encerrada?

Pregunta 6. El radio de un círculo aumenta a razón de 0,7 cm/s. ¿Cuál es la tasa de aumento de sus circunstancias?

Pregunta 7. La longitud x de un rectángulo disminuye a razón de 5 cm/minuto y el ancho y aumenta a razón de 4 cm/minuto. Cuando x = 8 cm y y = 6 cm, encuentre las tasas de cambio de (a) el perímetro yb) el área del rectángulo.

Pregunta 8. Un globo, que siempre permanece esférico al inflarse, se infla bombeando 900 centímetros cúbicos de gas por segundo. Encuentre la tasa a la que aumenta el radio del globo cuando el radio es de 15 cm.

Pregunta 9. Un globo, en el que siempre permanece esférico, tiene un radio variable. Encuentre la tasa a la que su volumen aumenta con el radio cuando el último es de 10 cm.

Pregunta 10. Una escalera de 5 m de largo está apoyada contra una pared. La parte inferior de la escalera se tira por el suelo, alejándola de la pared, a razón de 2 cm/s. ¿Qué tan rápido disminuye su altura sobre la pared cuando el pie de la escalera está a 4 m de la pared?

Pregunta 11. Una partícula se mueve a lo largo de la curva 6y=x 3 + 2. Encuentra los puntos en la curva en los que la coordenada y cambia 8 veces más rápido que la coordenada x.

Pregunta 12. El radio de una burbuja de aire aumenta a razón de 1/2 cm/s. ¿A qué tasa aumenta el volumen de la burbuja cuando el radio es de 1 cm?

Pregunta 13. Un globo, que siempre permanece esférico, tiene un diámetro variable (2x+1). Encuentre la tasa de cambio de su volumen con respecto a x.

Pregunta 14. Sale arena de un tubo a razón de 12 cm 3 /s. La arena que cae forma un cono en el suelo de tal manera que la altura del cono es siempre un sexto del radio de la base. ¿Qué tan rápido aumenta la altura del cono cuando la altura es de 4 cm?

Pregunta 15. El costo total C(x) en rupias asociado con la producción de x unidades de un artículo está dado por C(x)=0.003x 2 +15x+4000. Encuentre el costo marginal cuando se producen 17 unidades.

Pregunta 16. El ingreso total en rupias de la escala de x unidades de un producto viene dado por R(x)=13x 3 +26x+15. Encuentre el ingreso marginal cuando x=7.

Pregunta 17. La tasa de cambio del área del círculo con respecto a su radio r en r= 6cm es (A) 10π (B) 12π (C) 8π (D) 11π.

Pregunta 18. El ingreso total en rupias recibido por la venta de x unidades de un producto viene dado por R(x)=3x 2 +36x+5. El ingreso marginal, cuando x=15 es (A) 116 (B) 96 (C) 90 (D) 126

Deja una respuesta Cancelar la respuesta

Pregunta 2. El volumen de un cubo aumenta a razón de cm ³ /s. ¿Qué tan rápido aumenta el área de la superficie cuando la longitud de un borde es de 12 cm?

Pregunta 11. Una partícula se mueve a lo largo de la curva 6y=x ³ + 2. Encuentra los puntos en la curva en los que la coordenada y cambia 8 veces más rápido que la coordenada x.

Pregunta 13. Un globo, que siempre permanece esférico, tiene un diámetro variable $\frac{3}{2}$ (2x+1). Encuentre la tasa de cambio de su volumen con respecto a x.

Pregunta 14. Sale arena de un tubo a razón de 12 cm ³ /s. La arena que cae forma un cono en el suelo de tal manera que la altura del cono es siempre un sexto del radio de la base. ¿Qué tan rápido aumenta la altura del cono cuando la altura es de 4 cm?

Pregunta 15. El costo total C(x) en rupias asociado con la producción de x unidades de un artículo está dado por C(x)=0.003x ² +15x+4000. Encuentre el costo marginal cuando se producen 17 unidades.

Pregunta 16. El ingreso total en rupias de la escala de x unidades de un producto viene dado por R(x)=13x ³ +26x+15. Encuentre el ingreso marginal cuando x=7.

Pregunta 18. El ingreso total en rupias recibido por la venta de x unidades de un producto viene dado por R(x)=3x ² +36x+5. El ingreso marginal, cuando x=15 es (A) 116 (B) 96 (C) 90 (D) 126