Capítulo 6 Aplicación de Derivadas – Ejercicio 6.2| Serie 1
Pregunta 11. Demostrar que la función f dada por f(x) = x 2 – x + 1 no es estrictamente creciente ni decreciente en (– 1, 1).
Solución:
Dado: f(x) = x 2 – x + 1
f'(x) = 2x – 1
Para estrictamente creciente, f'(x) > 0
2x – 1 > 0
X > 1/2
Entonces, la función f(x) es creciente para x > 1/2 en el intervalo (1/2, 1) -(El intervalo dado es (-1, 1)
De manera similar, para decrecer f'(x) < 0
2x – 1 < 0
X < 1/2
Entonces, la función f(x) es creciente para x < 1/2 en el intervalo (-1, 1/2) -(El intervalo dado es (-1, 1)
Por lo tanto, la función f(x) = x 2 – x + 1 no es estrictamente creciente ni decreciente.
Pregunta 12. ¿Cuáles de las siguientes funciones son decrecientes en (0, π/2).
(A) cos x (B) cos 2x (C) cos 3x (D) tan x
Solución:
(A) f(x) = cos x
f'(x) = -sen x
Ahora en el intervalo (0, π/2), sen x es positivo (porque es el segundo cuadrante)
Entonces, -sen x < 0
∴ f'(x) < 0
f(x) = cos x es estrictamente decreciente en(0, π/2).
(B) f(x) = cos 2x
f'(x) = -2 sen 2x
Ahora en el intervalo (0, π/2), sen x es positivo (porque es el segundo cuadrante)
-sen 2x < 0
∴ f'(x) < 0,
f(x) = cos 2x es estrictamente decreciente en(0, π/2).
(C) f(x) = cos 3x
f'(x) = -3sen 3x
Sea 3x = t
Entonces en sen 3x = sen t
Cuando t ∈(0, π), sen t + >0 o 3x ∈ (0, π)
Pero cuando π/3 < x < π/2
π < 3x < 3π/2
Aquí sen 3x < 0
Entonces, en x ∈ (0, π/3),
f'(x) = -3sen 3x < 0 & en x∈(π/3, π/2), f'(x) = -3sen 3x > 0
f'(x) está cambiando de signo, por lo que f(x) no es estrictamente decreciente.
(D) f(x) = tan x
f'(x) = segundo 2 x
Ahora en x ∈ (0, π/2), sec 2 x > 0
Por lo tanto, f(x) es estrictamente creciente en (0, π/2).
Entonces, las opciones (A) y (B) son decrecientes en (0, π/2).
Pregunta 13. ¿En cuál de los siguientes intervalos es decreciente la función f dada por f(x) = x 100 + sen x – 1?
(A) (0, 1) (B) π/2, π (C) 0, π/2 (D) Ninguno de estos
Solución:
f(x) = x 100 + sen x – 1
f'(x) = 100x 99 + cos x
(A) En el intervalo (0, 1), x > 0, entonces 100x 99 > 0
y para cos x: (0, 1°) = (0, 0,57°) > 0
Por lo tanto, f(x)es estrictamente creciente en el intervalo(0, 1)
(B) En (π/2, π) intervalo,
Para 100x 99 : x ∈ (π/2, π) = (11/7, 22/7) = (1.5, 3.1) > 1
Entonces, x 99 > 1. Por lo tanto, 100x 99 > 100
Para Cos x: (π/2, π) en el segundo cuadrante y en el segundo cuadrante cos x es negativo, entonces el valor está en -1 y 0.
Por lo tanto, f(x)es estrictamente creciente en el intervalo (π/2, π)
(C) En el intervalo (0, π/2), tanto cos x > 0 como 100x 99 > 0
Entonces f'(x) > 0
Por lo tanto, f(x)es estrictamente creciente en el intervalo (0, π/2)
Entonces, la opción correcta es (D).
Pregunta 14. ¿Para qué valores de a la función f dada por f(x) = x 2 + ax + 1 es creciente en (1, 2)?
Solución:
Dado: f(x) = x 2 + ax + 1
f'(x) = 2x + a
Ahora, x ∈ (1, 2), 2x ∈ (2, 4)
2x + un ∈ (2 + un, 4 + un)
Para que f(x) sea estrictamente creciente, f'(x) > 0
Si el valor mínimo de f'(x) > 0 entonces
f'(x) en todo su dominio será > 0.
f'(x) min > 0
2 + a > 0
a > -2
Pregunta 15. Sea I cualquier intervalo disjunto de [–1, 1]. Demostrar que la función f dada por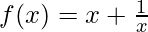 
es creciente en I.
Solución:
Claramente el intervalo máximo I es R-(-1,1)
Ahora, f(x) =
f'(x) =
Se da que I sea cualquier intervalo disjunto de [–1, 1]
Entonces, para cada x ∈ I o x < -1 o x > 1
Entonces, para x < -1, f'(x) es positivo.
Entonces, para x < 1, f'(x) es positiva.
Por lo tanto, f'(x) > 0 ∀ x ∈ I, entonces, f(x) es estrictamente creciente en I.
Pregunta 16. Demuestra que la función f dada por f(x) = log sen x es creciente en (0, π/2) y decreciente en (π/2, π).
Solución:
f(x) = log sen x
f'(x) =
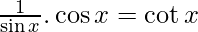
Intervalo (0, π/2), es primer cuadrante, aquí cot x es positivo.
Entonces, f'(x) = cot x es positivo (es decir, cot x > 0)
Por lo tanto, f(x) es estrictamente creciente en el intervalo (0, π/2)
Intervalo (π/2, π), es segundo cuadrante, aquí cot x es negativo.
Entonces, f'(x) = cot x es negativo (es decir, cot x < 0)
Por lo tanto, f(x) es estrictamente decreciente en el intervalo (π/2, π)
Pregunta 17. Demuestra que la función f dada por f(x) = log|cos x| es decreciente en (0, π/2) y creciente en (π/2, π).
Solución:
f(x) = logaritmo cos x
f'(x) = 1/cos x (-sen x) = -tan x
Intervalo (0, π/2), es el primer cuadrante, aquí tan x es positivo.
Entonces, f'(x) = -tan x es negativo (es decir, tan x < 0)
Por lo tanto, f(x) es estrictamente decreciente en el intervalo (0, π/2)
Intervalo (π/2, π), es el segundo cuadrante, aquí tan x es negativo.
Entonces, f'(x) = -tan x es positivo (es decir, tan x > 0)
Por lo tanto, f(x) es estrictamente creciente en el intervalo (π/2, π)
Pregunta 18. Demuestra que la función dada por f(x) = x 3 – 3x 2 + 3x – 100 es creciente en R.
Solución:
f(x) = x 3 – 3x 2 + 3x – 100
f'(x) = 3x 2 – 6x + 3
f'(x) = 3(x 2 – 2x + 1)
f'(x) = 3(x – 1) 2 ≥ 0 ∀ x en R
Entonces f(x) es estrictamente creciente en R.
Pregunta 19. El intervalo en el que y = x 2 e -x es creciente es
(A) (– ∞, ∞) (B) (– 2, 0) (C) (2, ∞) (D) (0, 2)
Solución:
Dado, f(x) = x 2 e -x
f'(x) = x 2 (-e -x ) + e -x .2x
f'(x) = e -x (2x – x 2 )
f'(x) = e -x .x(2 – x)
Para que f(x) sea creciente, f'(x) ≥ 0
Entonces, f'(x) ≥ 0
e -x .x.(2 – x) ≥ 0
x.(2 – x) ≥ 0
x(x – 2) ≥ 0
x ∈ [0, 2]
Entonces, f(x) es estrictamente creciente en el intervalo (0, 2). Opción correcta en D.
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA