Soluciones NCERT Clase 12 – Matemáticas Parte I – Aplicación de Derivadas – Ejercicio 6.2

Pregunta 1. Demuestre que la función dada por f (x) = 3x + 17 es creciente en R.

Solución:

Si para una función f(x), f'(x) > 0 para todo x, entonces la función es estrictamente creciente. (viceversa no es cierto)

Dado: f(x) = 3x + 17

f'(x) = 3 > 0 -(Siempre mayor que cero)

Por tanto, 3x + 17 es estrictamente creciente en R.

Pregunta 2. Muestre que la función está dada por f (x) = e ^2x es creciente en R.

Solución:

Si para una función f(x), f'(x) > 0 para todo x, entonces la función es estrictamente creciente. (viceversa no es cierto)

Dado: f(x) = e ^2x

f'(x) = 2e ^2x > 0

Por lo tanto, f(x) = e ^2x es estrictamente creciente en ∞

Pregunta 3. Demuestra que la función dada por f (x) = sen x es

(i) aumentando en (0, π/2)

(ii) decretando en (π/2, π)

(iii) ni creciente ni decreciente en (0, π)

Solución:

Dado: f(x) = sen x

Entonces, f'(x) = d/dx(sen x) = cos x

(i) Ahora en (0, π/2), f'(x) = cos x > 0 (positivo en el primer cuadrante)

Por lo tanto, f(x) = sen x es estrictamente creciente en (0, π/2).

(ii) En (π/2, π), f'(x) = cos x < 0 -(negativa en el segundo cuadrante)

Por lo tanto, f(x) = sen x es estrictamente decreciente en (π/2,π)

(iii) Como sabemos que f'(x) = cos x es positivo en el intervalo (0, π/2)

y f'(x) = cos x es negativo en el intervalo (π/2, π)

Por lo tanto, no es ni creciente ni decreciente.

Pregunta 4. Encuentra los intervalos en los que la función f dada por f(x) = 2x ² – 3x es

(yo) aumentando

(ii) decreciente

Solución:

Dado: f(x) = 2x ² – 3x

f'(x) = $\frac{d(2x^2-3x)}{dx}$ = 4x – 3 -(1)

= x = 3/4

Entonces los intervalos son (-∞, 3/4) y (3/4, ∞)

(i) Intervalo (3/4, ∞) sea x = 1

Entonces, de la ecuación (1) f'(x) > 0

Por lo tanto, f es estrictamente creciente en el intervalo (3/4, ∞)

(ii) Intervalo (-∞, 3/4) sea x = 0.5

Entonces, de la ecuación (1) f'(x) < 0

Por lo tanto, f es estrictamente decreciente en el intervalo (-∞, 3/4)

Pregunta 5. Encuentra los intervalos en los que la función f dada por f(x) = 2x ³ – 3x ² – 36x + 7 es

(yo) aumentando

(ii) decreciente

Solución:

Dado: f(x) = 2x ³ – 3x ² – 36x + 7

f'(x) = $\frac{d(2x^3-3x^2-36x+7)}{dx}$ = 6x ² – 6x – 36 -(1)

f'(x) = 6(x ² – x – 6)

Al poner f'(x) = 0, obtenemos

6(x ² – x – 6) = 0

(x ² – x – 6) = 0

x = -2, x = 3

Entonces, los intervalos son (-∞, -2), (-2, 3) y (3, ∞)

Para (-∞, -2) intervalo, tome x = -3

De la ecuación (1), obtenemos

f'(x) = (+)(-)(-) = (+) > 0

Entonces, f es estrictamente creciente en el intervalo (-∞, -2)

Para el intervalo (-2, 3), tome x = 2

De la ecuación (1), obtenemos

f'(x) = (+)(+)(-) = (-) < 0

Entonces, f es estrictamente decreciente en el intervalo (-2, 3)

Para (3, ∞)intervalo, tome x = 4

De la ecuación (1), obtenemos

f'(x) = (+)(+)(+) = (+) > 0

Entonces, f es estrictamente creciente en el intervalo (3, ∞)

(i) f es estrictamente creciente en el intervalo (-∞, -2) y (3, ∞)

(ii) f es estrictamente decreciente en el intervalo (-2, 3)

Pregunta 6. Encuentra los intervalos en los que las siguientes funciones son estrictamente crecientes o decrecientes:

(i) x ² + 2x – 5

(ii) 10 – 6x – 2x ²

(iii) -2x ³ – 9x ² – 12x + 1

(iv) 6 – 9x – x ²

(v) (x + 1) ³ (x – 3) ³

Solución:

(i) f(x) = x2 ⁺ 2x – 5

f'(x) = 2x + 2 -(1)

Al poner f'(x) = 0, obtenemos

2x + 2 = 0

x = -1

Entonces, los intervalos son (-∞, -1) y (-1, ∞)

Para (-∞, -1) intervalo tomar x = -2

De la ecuación (1), f'(x) = (-) < 0

Entonces, f es estrictamente decreciente

Para (-1, ∞) intervalo tomar x = 0

De la ecuación (1), f'(x) = (+) > 0

Entonces, f es estrictamente creciente

(ii) f(x) = 10 – 6x – 2x ²

f'(x) = -6 – 4x

Al poner f'(x) = 0, obtenemos

-6 – 4x = 0

x = -3/2

Entonces, los intervalos son (-∞, -3/2) y (-3/2, ∞)

Para (-∞, -3/2) intervalo tomar x = -2

De la ecuación (1), f'(x) = (-)(-) = (+) > 0

Entonces, f es estrictamente creciente

Para (-3/2, ∞) intervalo tomar x = -1

De la ecuación (1), f'(x) = (-)(+) = (-) < 0

Entonces, f es estrictamente decreciente

(iii) f(x) = -2x ³ – 9x ² – 12x + 1

f'(x) = -6x ² – 8x – 12

Al poner f'(x) = 0, obtenemos

-6x ² – 8x – 12 = 0

-6(x + 1)(x + 2) = 0

X = -1, X = -2

Entonces, los intervalos son (-∞, -2), (-2, -1) y (-1, ∞)

Para (-∞, -2) intervalo tomar x = -3

De la ecuación (1), f'(x) = (-)(-)(-) = (-) < 0

Entonces, f es estrictamente decreciente

Para (-2, -1) intervalo tomar x = -1.5

De la ecuación (1), f'(x) = (-)(-)(+) = (+) > 0

Entonces, f es estrictamente creciente

Para (-1, ∞) intervalo tomar x = 0

De la ecuación (1), f'(x) = (-)(+)(+) = (-) < 0

Entonces, f es estrictamente decreciente

(iv) f(x) = 6 – 9x – x ²

f'(x) = -9 – 2x

Al poner f'(x) = 0, obtenemos

-9 – 2x = 0

x = -9/2

Entonces, los intervalos son (-∞, -9/2) y (-9/2, ∞)

Para que f sea estrictamente creciente, f'(x) > 0

– 9 – 2x > 0

x > -9/2

Entonces f es estrictamente creciente en el intervalo (-∞, -9/2)

Para que f sea estrictamente decreciente, f'(x) < 0

-9 – 2x < 0

x < -9/2

Entonces f es estrictamente decreciente en el intervalo (-9/2, ∞)

(v) f(x) = (x + 1) ³ (x – 3) ³

f'(x) = (x + 3) ³ .3(x – 3) ³ + (x – 3) ³ .3(x + 1) ²

f'(x) = 6(x – 3) ² (x + 1) ² (x – 1)

Ahora, el factor de (x – 3) ² y (x + 1) ² no son negativos para todo x

Para que f sea estrictamente creciente, f'(x) > 0

(x – 1) > 0

X > 1

Entonces, f es estrictamente creciente en el intervalo (1, ∞)

Para que f sea estrictamente decreciente, f'(x) < 0

(x – 1) < 0

xo < 1

Entonces, f es estrictamente decreciente en el intervalo (-∞, 1)

Pregunta 7. Muestre que y = log(1 + x) – 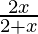$\frac{2x}{2+x}$ , es una función creciente de x en todo su dominio.

Solución:

f(x) = registro(1+x) $\frac{-2x}{2+x}, x>-1$

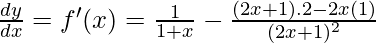
$\frac{dy}{dx}=f'(x)=\frac{1}{1+x}-\frac{(2x+1).2-2x(1)}{(2x+1)^2}$

f'(x)= $\frac{1}{1+x}-\frac{4+2x-2x}{(2x+1)^2}$

$f'(x)=\frac{1}{1+x}-\frac{4}{(2+x)^2}$

$f'(x)=\frac{(x+2)^2-4(x+1)}{(x+1)(x+2)}$

$f'(x)=\frac{x^2}{(x+1)(x+2)^2}$

Entonces, el dominio de la función dada es x > -1

Ahora, x ² > 0, (x + 2) ² ≥ 0, x + 1 > 0

De la ecuación anterior f'(x) ≥ 0 ∀ x en el dominio (x > -1) y f es una función creciente.

Pregunta 8. Encuentra los valores de x para los cuales y = [x(x – 2)] ² es una función creciente.

Solución:

Dado: y = f(x) = [x(x – 2)] ² = x ² (x– 2x) ²

= x ⁴ – 4x ³ + 4x ²

f'(x) = 4x ³ – 12x ² + 8x

f'(x) = 4x(x – 2)(x – 1)

x = 0, x = 1, x = 2

Entonces, (∞, 0], [0, 1], [1, 2], [2, ∞)

Para (∞, 0], sea x = -1

Entonces, f'(x) = (-)(-)(-) = (-) ≤ 0

f(x) es decreciente

Para [0, 1], sea x = 1/2

Entonces, f'(x) = (+)(-)(-) = (+) ≥ 0

f(x) es creciente

De manera similar, para [1, 2], f(x) es decreciente

Para [2,∞), f(x) es creciente

Entonces, f(x) es creciente en el intervalo [0, 1] y [2,∞)

Pregunta 9. Demuestra que y = 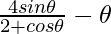$\frac{4sin\theta}{2+cos\theta}-\theta$ es una función creciente de θ en [0, π/2].

Solución:

y = f(θ) = $\frac{4\sinθ}{(2+\cosθ)^2}-θ$

$f'(θ)=\frac{(2+\cosθ).4\cosθ-4\sinθ(-\sinθ)}{(2+\cosθ)^2}$

$f'(θ)=\frac{4.(2\cosθ+\cos^2θ+\sin^2θ)}{(2+\cosθ)^2}-1$

$f'(θ)=\frac{8\cosθ+4}{(\cosθ+2)^2}$

$f'(θ)=\frac{8\cosθ+4-(2+\cosθ)^2}{(2+\cosθ)^2}$

$f'(θ)=\frac{4\cosθ-\cos^2θ}{(2+\cosθ)^2}$

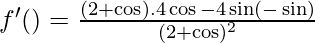
Ahora 0 ≤ θ ≤ π/2, y tenemos 0 ≤ cosθ ≤ 1,

Entonces, 4 – cosθ > 0

Por lo tanto f'(θ) ≥ 0 para 0 ≤ θ ≤ π/2

Por tanto, f'(x) = $\frac{4\sinθ}{2+\cosθ}-θ$ es estrictamente creciente en el intervalo (θ, π/2).

Pregunta 10. Demuestra que la función logarítmica es creciente en (0, ∞).

Solución:

Dado: f(x) = log(x) -(función logarítmica)

f'(x) = 1/x ∀ x en (0, ∞)

Por lo tanto, x > 0, entonces, 1/x > 0

Por lo tanto, la función logarítmica es estrictamente creciente en el intervalo (0, ∞)

Capítulo 6 Aplicación de Derivadas – Ejercicio 6.2 | conjunto 2

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Soluciones NCERT Clase 12 – Matemáticas Parte I – Aplicación de Derivadas – Ejercicio 6.2 | Serie 1

Pregunta 1. Demuestre que la función dada por f (x) = 3x + 17 es creciente en R.

Pregunta 2. Muestre que la función está dada por f (x) = e ^2x es creciente en R.

Pregunta 3. Demuestra que la función dada por f (x) = sen x es

(i) aumentando en (0, π/2)

(ii) decretando en (π/2, π)

(iii) ni creciente ni decreciente en (0, π)

Pregunta 4. Encuentra los intervalos en los que la función f dada por f(x) = 2x ² – 3x es

(yo) aumentando

(ii) decreciente

Pregunta 5. Encuentra los intervalos en los que la función f dada por f(x) = 2x ³ – 3x ² – 36x + 7 es

(yo) aumentando

(ii) decreciente

Pregunta 6. Encuentra los intervalos en los que las siguientes funciones son estrictamente crecientes o decrecientes:

(i) x ² + 2x – 5

(ii) 10 – 6x – 2x ²

(iii) -2x ³ – 9x ² – 12x + 1

(iv) 6 – 9x – x ²

(v) (x + 1) ³ (x – 3) ³

Pregunta 7. Muestre que y = log(1 + x) – $\frac{2x}{2+x}$ , es una función creciente de x en todo su dominio.

Pregunta 8. Encuentra los valores de x para los cuales y = [x(x – 2)] ² es una función creciente.

Pregunta 9. Demuestra que y = $\frac{4sin\theta}{2+cos\theta}-\theta$ es una función creciente de θ en [0, π/2].

Pregunta 10. Demuestra que la función logarítmica es creciente en (0, ∞).

Capítulo 6 Aplicación de Derivadas – Ejercicio 6.2 | conjunto 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. Demuestre que la función dada por f (x) = 3x + 17 es creciente en R.

Pregunta 2. Muestre que la función está dada por f (x) = e 2x es creciente en R.

Pregunta 3. Demuestra que la función dada por f (x) = sen x es

(i) aumentando en (0, π/2)

(ii) decretando en (π/2, π)

(iii) ni creciente ni decreciente en (0, π)

Pregunta 4. Encuentra los intervalos en los que la función f dada por f(x) = 2x 2 – 3x es

(yo) aumentando

(ii) decreciente

Pregunta 5. Encuentra los intervalos en los que la función f dada por f(x) = 2x 3 – 3x 2 – 36x + 7 es

(yo) aumentando

(ii) decreciente

Pregunta 6. Encuentra los intervalos en los que las siguientes funciones son estrictamente crecientes o decrecientes:

(i) x 2 + 2x – 5

(ii) 10 – 6x – 2x 2

(iii) -2x 3 – 9x 2 – 12x + 1

(iv) 6 – 9x – x 2

(v) (x + 1) 3 (x – 3) 3

Pregunta 7. Muestre que y = log(1 + x) – , es una función creciente de x en todo su dominio.

Pregunta 8. Encuentra los valores de x para los cuales y = [x(x – 2)] 2 es una función creciente.

Pregunta 9. Demuestra que y = es una función creciente de θ en [0, π/2].

Pregunta 10. Demuestra que la función logarítmica es creciente en (0, ∞).

Capítulo 6 Aplicación de Derivadas – Ejercicio 6.2 | conjunto 2

Deja una respuesta Cancelar la respuesta

Pregunta 2. Muestre que la función está dada por f (x) = e ^2x es creciente en R.

Pregunta 4. Encuentra los intervalos en los que la función f dada por f(x) = 2x ² – 3x es

Pregunta 5. Encuentra los intervalos en los que la función f dada por f(x) = 2x ³ – 3x ² – 36x + 7 es

(i) x ² + 2x – 5

(ii) 10 – 6x – 2x ²

(iii) -2x ³ – 9x ² – 12x + 1

(iv) 6 – 9x – x ²

(v) (x + 1) ³ (x – 3) ³

Pregunta 7. Muestre que y = log(1 + x) – $\frac{2x}{2+x}$ , es una función creciente de x en todo su dominio.

Pregunta 8. Encuentra los valores de x para los cuales y = [x(x – 2)] ² es una función creciente.

Pregunta 9. Demuestra que y = $\frac{4sin\theta}{2+cos\theta}-\theta$ es una función creciente de θ en [0, π/2].