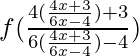Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 1 Relaciones y funciones – Ejercicio 1.3

Posted on by Rudeus Greyrat

Pregunta 1. Sean f : {1, 3, 4} -> {1, 2, 5} y g : {1, 2, 5} -> {1, 3} dadas por f = {(1, 2) , (3, 5), (4, 1) y g = {(1, 3), (2, 5), (5, 1)}. Anota gof.

Solución: 

f= {(1, 2), (3, 5), (4, 1)}

g= {(1, 3), (2, 3), (5, 1)}

f(1)= 2, g(2) = 3 => gof(1) = 3

f(3) = 5, g(5) = 1 => gof(3) = 1

f(4) =1, g(1) = 3 => gof(4) = 3 

=> golf = {(1,3), (3,1), (4,3)}

Pregunta 2. Sean f, g y h funciones de R a R. Demostrar que (f+g) oh = foh + goh, (f * g) oh = (foh) * (goh).

Solución:

f: R-> R, g: R-> R, h: R-> R

(f+g) oh(x) = (f+g) oh(x)

= (f+g) [h(x)]

= f[h(x)] + g[h(x)]

= foh(x) + goh(x)

(f+g) oh = foh + goh  

(f * g) oh (x) = (f * g) oh (x)

= (f * g) [h(x)]

= f[h(x)] * g[h(x)]

= foh(x) * goh (x)

(f * g) oh = (foh) * (goh)

Pregunta 3. Encuentra gof y niebla, si

(i) f(x) = |x| yg(x) = |5x – 2|

(ii) f(x) = 8x 3   y g(x) = x 1/3

Solución: 

(yo) Tenemos,        

f(x) = |x| yg(x) = | 5x – 2 |

gof(x) = g(f(x)) = g(|x|)

=> gof(x) = | 5 |x|-2 |

niebla(x) = f(g(x)) = f(|5x-2|)

=> niebla(x) = || 5x-2|| = | 5x -2 | 

(ii) Tenemos,

f(x) = 8x 3 y g(x) = x 1/3

gof(x) = g(f(x)) = g(8x 3 )

=> gof(x) = (8x 3 ) 1/3 = 2x

niebla(x) = f(g(x)) = f(x 1/3 )

=> niebla(x) = 8(x 1/3 ) 3 = 8x

Pregunta 4. Si f(x) = 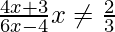 \frac{4x+3}{6x-4}x \neq \frac{2}{3}  , demuestre que fof(x) = x para todo  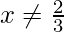x \neq \frac{2}{3}  . ¿Cuál es el inverso de f?

Solución:   

Dado que,

f (x) = \frac{4x+3}{6x-4}x \neq \frac{2}{3}

Ahora, 

fof(x) = f(f(x)) = f(\frac{4x+3}{6x-4})

= f(\frac{4(\frac{4x+3}{6x-4})+3}{6(\frac{4x+3}{6x-4})-4})

Al simplificar tomando MCM = (6x-4)

fo(x) =  \frac{16x + 12 + 18x - 12}{24x + 18 -24x + 16}

=> fof (x) =  \frac{34x}{34} = x 

=> fof(x) = I A (x) para todos x \neq \frac{2}{3}

=> fof(x) = I A tal que A = R –  {\frac{2}{3}}  que es el dominio de f

=> f -1 = f          

Por lo tanto, probado.

Pregunta 5. Indique con razón si las siguientes funciones tienen inversa. Encuentre la inversa, si existe.

(yo) f : {1, 2, 3, 4} -> {10}

con f = {(1, 10), (2, 10), (3,10), (4,10)}

(ii) g: {5, 6, 7, 8} -> {1, 2, 3, 4}

con g = {(5, 4), (6, 3), (7, 4), (8, 2)}

(iii) h : {2, 3, 4, 5} -> {7, 9, 11, 13}

con h : {(2, 7), (3, 9), (4, 11), (5, 13)}

Solución:

(i) Tenemos f(1) = f(2) = f(3) = f(4) = 10 lo que significa que f es muchos-uno 

y no uno-uno, por lo que la inversa de f no existe.

(ii) Aquí g(5) = g(7) =4, es decir, g es muchos-uno, por lo que el inverso de g no existe.

(iii) Dado que el rango de h = {7, 9, 11, 13} = codominio, por lo tanto, h es sobre,

Además, cada elemento de dominio tiene una imagen única en h, por lo tanto h es uno-uno.

Ahora, dado que h es tanto uno como sobre uno, entonces existe el inverso de h.

h -1 = {(7, 2), (9, 3), (11, 4), (13, 5)}

Pregunta 6. Demostrar que f : [-1, 1] -> R, dado por f(x) = 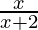 \frac{x}{x+2}  es uno-uno. Encuentra el inverso de la función f : {-1,1} -> Rango f.

Solución: 

Sean x, y  [-1, 1]   \in

f(x) =  \frac{x}{x+2}

f(y) = \frac{y}{y+2}

Ahora, 

Sea f(x) = f(y) 

\frac{x}{x+2} = \frac{y}{y+2}   

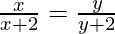
=> x(x+2) = y(x+2)

=> xy + 2x = xy + 2y

=> 2x = 2y

=> x = y

=> f es uno-uno

También,

X = [-1, 1] y,

Y = {  y \in R : y = \frac{x}{x+2} , x \in X  } = rango de f.

=> f está sobre

Como f es uno y sobre, entonces existe el inverso de f.

Sea y = f(x) => x =f -1 (y)

=> y = \frac{x}{x+2}            

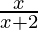
=> xy + 2y = x

=> 2y = x(1 – y)

=> x = \frac{2y}{1 - y}, y \ne 1

Por tanto, f : Y-> X está definida por f(y) =  \frac{2y}{1-y}, y \ne 1  .

Pregunta 7. Considere f : R -> R viene dado por f(x) = 4x + 3 . Demuestre que f es invertible. Encuentra el inverso de f.

Solución:

Se da que,

f(x) = 4x + 3 donde f : R -> R

Dejar, 

f(x) = f(y) 

=> 4x + 3 = 4y + 3

=> 4x = 4y

=> x = y

=> f es una función uno a uno 

También,

Sea y = 4x + 3 donde y  \in   R

=> x = \frac{y-3}{4}  \in R

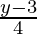
Ya que para cualquier  y \in R . existe  x = \frac{y-3}{4} \in R  tal que

f(x) =  f(\frac{y-3}{4}) = 4  (\frac{y-3}{4})  +3 = y

=> f está sobre

Dado que f es tanto uno como sobre uno, entonces existe f -1

=> f -1 (y) = \frac{y-3}{4}

Pregunta 8. Considere f : R + -> [4, 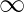 \infty  ) dada por f(x) = x 2 + 4. Demuestre que f es invertible con la inversa f -1 de f dada por f -1 (y) =  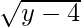\sqrt{ y -4} , donde R + es el conjunto de todos los números reales no negativos.

Solución: 

Sea f(x) = f(y)

=> x + 4 = y + 4

=> x2 = y2

=> x = y [ x,y  \in  R + ]

=> f es uno-uno

Sea y = x 2 + 4 donde y \in [4, \infty )

=> x 2 = y – 4  \geq  4 [ y \geq 4 ]

=> x = \sqrt{y -4}

Por lo tanto, para cualquier y  \in R  , existe x =  \sqrt{y-4}  \in R

=> f está sobre

Como f es tanto uno como sobre uno, f -1 existe para todo  y \geq 4 ,

=> f -1 (y) = \sqrt{y-4}

Pregunta 9. Considere R + -> [ -5, 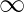 \infty ) dada por f (x) = 9x 2 + 6x -5. Demostrar que f es invertible con f -1 (y) =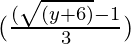 (\frac{(\sqrt{(y+6)}-1}{3})

Solución: 

Sea f(x) = f(y)

=> 9x 2 + 6x -5 = 9y 2 + 6y – 5

=> 9x 2 + 6x = 9y 2 + 6y

=> 9(x 2 – y 2 ) + 6 (x – y) = 0

=> (x – y) [9 (x + y) + 6] = 0

=> x – y =0

=> x = y

=> f es uno-uno

Ahora, sea y = 9x 2 + 6x – 5

=> 9x 2 + 6x – 5 (x + y) = 0

=> x = \frac{-6 \pm \sqrt{6*6 + 4*9(5+y)} }{18} = \frac{\sqrt{(y+6)}-1}{3}   

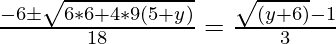
=> f(x) = f(\frac{\sqrt{(y+6)}-1}{3}) = 9 (\frac{\sqrt{(y+6)}-1}{3})^{2}+(\frac{\sqrt{(y+6)}-1}{3}) -5

Al simplificar, tenemos f (x) = y 

=> f está sobre

Dado que f es tanto uno como sobre uno. f -1 existe

f -1 (y) = \frac{\sqrt{(y+6)}-1}{3}

Pregunta 10. Sea f : X -> Y una función invertible. Demostrar que f tiene inversa única. 

Solución:

Tenemos,

f : X -> Y es una función invertible

Sean g y h dos inversos distintos de f.

Entonces, para todo y \in  Y,

niebla (y) = yo (y) = foh (y)

=> fg (y)) = f(h (y))

=> g(y) = h(y) [f es uno-uno]

=> g = h [g es uno-uno]

lo que contradice nuestra suposición. 

Por lo tanto, f tiene un único inverso.

Pregunta 11. Considere f : {1, 2, 3} -> {a, b, c} dada por f (1) = a, f (2) = b, f (3) = c. Encuentre f y demuestre que (f -1 )f -1 = f.

Solución:

Dado que,

f(1) = una, f(2) = segundo, f(3) = c

Tenemos,

f = {(1, a), (2, b), (c, 3)}

lo que muestra que f es tanto uno como sobre uno y, por lo tanto, f es invertible.

Por lo tanto,

f -1 = {(a, 1), (b, 2), (c, 3)} 

También,

(f -1 ) -1 = {(1, a), (2, b), (3, c)}

=> (f -1 ) -1 = f 

Por lo tanto probado.

Pregunta 12. Sea f: X -> Y una función invertible. Muestre que el inverso de f -1 es f, es decir, (f -1 ) -1 = f.

Solución:

Como f es una función invertible,

=> f es a la vez uno-uno y sobre

También,

Sea g : Y -> X , donde g es una función uno y sobre tal que

gof (x) = yo x y niebla (y) = yo y => g = f -1

=> f -1 o (f -1 ) -1 = yo

=> fo [f -1 o (f -1 ) -1 ] = fo I

=> (fo -1 ) o (f -1 ) -1 = f 

=> Yo o (f -1 ) -1 = f

Por lo tanto, (f -1 ) -1 = f

Pregunta 13. Si f : R -> R dada por f (x) = (3 – x 3 ) 1/3 , entonces fof (x) es:

(A) x 1/3                      (B) x 3                     (C) x. (D) (3 – x 3 )

Solución:

Respuesta: (C)

Tenemos,

f(x) = (3 – x 3 ) 1/3           donde f : R -> R

Ahora,

fof(x) = f(f(x))

=> fof(x) = f((3 – x 3 ) 1/3 ) 

=> fo(x) = [3 – ((3 – x 3 ) 1/3 ) 3 ] 1/3  

=> fo(x) = [3 – (3 – x 3 )] 1/3              

=> fo(x) = (x 3 ) 1/3

=> fo(x) = x

Por lo tanto, la opción C es correcta.

Pregunta 14. Sea f : R -{ 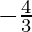 -\frac{4}{3} } -> R una función definida como f(x) =  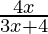\frac{4x}{3x+4}  . El inverso de f es el mapa g : Rango f -> R – {  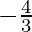-\frac{4}{3}  } dado por

(A) g(y) =  \frac{3y}{3-4y}                                               (B) g(y) = \frac{4y}{4-3y}

(C) g(y) =  \frac{4y}{3-4y}                                               (D) g(y) = \frac{3y}{4-3y}

Solución:

Respuesta: (B)

Sea y = f(x)

=> y = \frac{4x}{3x+4}

=> 3xy + 4y = 4x

=> x( 4 – 3y) = 4y

=> x = \frac{4y}{4-3y}  

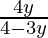
f -1 (y) = g (y) = \frac{4y}{4-3y}

Publicación traducida automáticamente

Artículo escrito por sarthaksaxena9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *