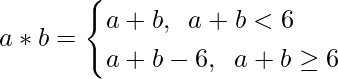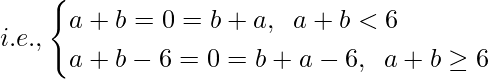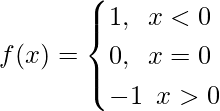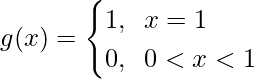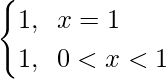Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 1 Relaciones y funciones – Ejercicio misceláneo en el Capítulo 1 | conjunto 2

Pregunta 11: Sean S = {a, b, c} y T = {1, 2, 3}. Encuentre F ^–1 de las siguientes funciones F de S a T, si existe.

(i) F = {(a, 3), (b, 2), (c, 1)} 

Solución:

Como, F = {(a, 3), (b, 2), (c, 1)} y S = {a,b,c} y T={1,2,3}

F: S→T se define como

F(a) = 3, F(b) = 2 y F(c) = 1

F es uno-uno y sobre.

Tomando F ^-1 , entonces F ^-1 : T→S

a = F ^-1 (3), b = F ^-1 (2) y c = F ^-1 (1)

F – ¹ = {(3,a),(2,b),(1,c)}

(ii) F = {(a, 2), (b, 1), (c, 1)}

Solución:

Como, F = {(a, 2), (b, 1), (c, 1)}

F: S→T se define como

F(a) = 2, F(b) = 1 y F(c) = 1

Aquí, F(b) = F(c) pero b ≠ c

Por lo tanto, F no es uno-uno.

Entonces, F no es invertible y F ^-1 no existe.

Pregunta 12. Considere las operaciones binarias ∗ : R × R → R y o : R × R → R definidas como a ∗b = |a – b| y aob = a, ∀ a, b ∈ R. Demuestre que ∗ es conmutativo pero no asociativo, o es asociativo pero no conmutativo. Además, demuestre que ∀ a, b, c ∈ R, a ∗ (boc) = (a ∗ b) o (a ∗ c). [Si es así, decimos que la operación ∗ reparte sobre la operación o]. ¿Se distribuye sobre ∗? Justifica tu respuesta.

Solución:

Operaciones binarias ∗ : R × R → R definida como a ∗b = |a – b|

a*b = |ab|

b*a = |ba| = |-(ab)| = |ab|

a*b = b*a

Por lo tanto, ∗ es conmutativo.

Ahora, tomemos a=1, b=2 y c=3 para una mejor comprensión

a*(b*c) = a*|bc| = |a-|bc|| = |1-|2-3|| = 0

(a*b)*c = |ab|*c = ||ab|-c| = ||1-2|-3| = 2

a*(b*c) ≠ (a*b)*c

Por lo tanto, ∗ no es asociativo.

Operaciones binarias o : R × R → R definidas como aob = a, ∀ a, b ∈ R

aob = un

boa = b

aob ≠ boa

Por lo tanto, o no es conmutativo.

ao (boc) = aob = a

(aob) oc = aoc = a

ao (boc) ≠ (aob) oc

Por lo tanto, o es asociativo.

Comprobemos si a ∗ (boc) = (a ∗ b) o (a ∗ c) a, b, c ∈ R

a ∗ (boc) = a * b = |ab|

(a ∗ b) o (a ∗ c) = |ab| o |ca| = |ab|

Por tanto, a ∗ (boc) = (a ∗ b) o (a ∗ c)

Ahora, busquemos ao (b * c) = (aob) * (aoc)

ao (b * c) = un

(aob) * (aoc) = a * a = |aa| = 0

Por lo tanto, ao (b * c) ≠ (aob) * (aoc)

o no se distribuye sobre ∗

Pregunta 13. Dado un conjunto X no vacío, sea ∗ : P(X) × P(X) → P(X) definido como A * B = (A – B) ∪ (B – A), ∀ A, B ∈ P(X). Muestre que el conjunto vacío φ es la identidad de la operación ∗ y que todos los elementos A de P(X) son invertibles con A ^–1 = A. 

(Pista: (A – φ) ∪ (φ – A) = A y (A – A) ∪ (A – A) = A ∗ A = φ).

Solución:

Conjunto X, tal que P(X) × P(X) → P(X) se define como A * B = (A – B) ∪ (B – A), ∀ A, B ∈ P(X)

φ*A = (φ-A) U (A-φ) = φ UA = A

A*φ = (A-φ) U (φ-A) = AU φ = A

Por lo tanto, φ es el elemento de identidad para la operación * en P(X)

A*A = (AA) U (AA) = φ U φ = φ

⇒ A = A ^-1

Por tanto, todos los elementos A de P(X) son invertibles con A ^–1 = A. 

Pregunta 14. Defina una operación binaria ∗ en el conjunto {0, 1, 2, 3, 4, 5} como 

Muestre que cero es la identidad para esta operación y que cada elemento a ≠ 0 del conjunto es invertible con 6, siendo a el inverso de a.

Solución:

Sea el conjunto x = {0, 1, 2, 3, 4, 5}

Tomemos i como elemento de identidad, donde a*i = a = i*a ∀ a ∈ x

un*0 = un

0*a = a, cuando (a+0<6)

Por lo tanto, cero es la identidad para esta operación.

Un elemento a ∈ x es invertible si existe b ∈ x tal que a*b = b*a = 0

De las ecuaciones anteriores, tenemos

a = -b o b = 6-a

Pero, como x = {0, 1, 2, 3, 4, 5} y a,b∈ x. Entonces a≠-b

Por lo tanto, b = 6-a es el inverso de un elemento a∈ x

a≠0

a – ¹ = 6-a

Pregunta 15. Sean A = {– 1, 0, 1, 2}, B = {– 4, – 2, 0, 2} y f, g : A → B funciones definidas por f(x) = x ² – x, x ∈ A y 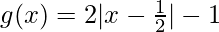  x ∈ A. ¿F y g son iguales? Justifica tu respuesta. 

(Pista: se puede notar que dos funciones f : A → B y g : A → B tales que f(a) = g (a) ∀ a ∈ A, se llaman funciones iguales).

Solución:

Dado, f, g : A → B ser funciones definidas por f(x) = x ² – x, x ∈ A y g(x) =    x ∈ A

En x = -1

f(0) = (-1) ² – (-1) = 2

g(0) =   = 2

Aquí, f(-1) = g(-1) y 2=2

En x = 0

f(0) = 0 ² – 0 = 0

g(0) =   = 0

Aquí, f(0) = g(0) y 0=0

En x = 1

f(1) = 1 ² – 1 = 0

g(1) =   = 0

Aquí, f(1) = g(1) y 1=1

En x = 2

f(1) = 2 ² – 2 = 2

g(1) =   = 2

Aquí, f(2) = g(2) y 2=2

Para todo c∈ A, f(c) = g(c)

Por lo tanto, f y g son funciones iguales.

Pregunta 16. Sea A = {1, 2, 3}. Entonces el número de relaciones que contienen (1, 2) y (1, 3) que son reflexivas y simétricas pero no transitivas es

(A) 1 

(B) 2 

(C) 3 

(D) 4

Solución:

R = {(1,1),(1,2),(1,3),(2,1),(2,2),(3,1),(3,3)}

Reflexivo : (1,1), (2,2), (3,3) ∈ R

Simétrico: (1,2), (2,1)∈ R y (1,3), (3,1) ∈ R

R no es Transitiva porque, (1,2), (1,3) ∈ R pero (3,2) ∉R

Entonces, si sumamos (3,2) y (2,3) o ambos, entonces R se volverá transitivo.

Nuevo, R = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3, 2),(3,3)}

Por lo tanto, A es la opción correcta.

Pregunta 17. Sea A = {1, 2, 3}. Entonces el número de relaciones de equivalencia que contienen (1, 2) es

(A) 1 

(B) 2 

(C) 3 

(D) 4

Solución:

Relaciones de equivalencia más pequeñas que contienen (1, 2):

R = {(1,1),(2,2),(1,2),(2,1),(3,3)}

o R = {(1,1),(2,2),(1,2),(2,1),(3,2),(2,3)(3,3)}

Por lo tanto, B es la opción correcta.

Pregunta 18. Sea f : R → R la Función Signum definida como

y g : R → R sea la función de mayor entero dada por g (x) = [x], donde [x] es el mayor entero menor o igual que x. Entonces, ¿la niebla y el gof coinciden en (0, 1]?

Solución:

Dado, f : R → R y g : R → R

cuando x ∈ (0,1]

[x] = 1, cuando x=1

[x] = 0, cuando 0<x<1

Ahora, niebla(x)=f(g(x)) = f([x])

 

Y ahora gof(x) = g(f(x))

g(1) = [1] = 1

g(0) = [0] = 0

g(-1) = [-1] = -1

Cuando x ∈ (0,1), fog = 0 y gof = 1. fog(1) ≠ gof(1)

Por tanto, fog y gof no coinciden en (0, 1).

Pregunta 19. Número de operaciones binarias en el conjunto {a, b} son

(A) 10 

(B) 16 

(C) 20 

(D) 8

Solución:

Sea A = {a,b}

A x A = {a,b} x {a,b}

R = {(a,a),(a,b),(b,a),(b,b)}

El número de elementos es 4.

Por lo tanto, el número de operaciones binarias en el conjunto será 2 ⁴ = 16

Por lo tanto, B es la opción correcta.