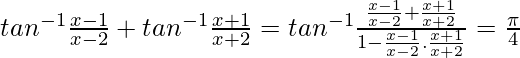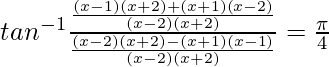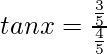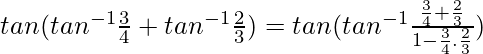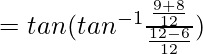Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 2 Funciones trigonométricas inversas – Ejercicio 2.2

Capítulo 2 Funciones trigonométricas inversas – Ejercicio 2.2 | Serie 1

Encuentre los valores de cada uno de los siguientes:

Pregunta 11. tan ⁻¹ [2cos(2sen ⁻¹ 1/2)]

Solución:

Supongamos que sen ⁻¹ 1/2 = x

Entonces, senx = 1/2

Por lo tanto, x = π /6 = sen ⁻¹ 1/2

Por lo tanto, tan ⁻¹ [2 cos (2 sin ⁻¹ 1/2)] = tan ⁻¹ [2 cos(2 * π /6)]

= tan ⁻¹ [2cos( π /3)]

Además, coseno ( π/3 ) = 1/2

Por lo tanto, tan ⁻¹ [2cos( π /3)] = tan ⁻¹ [(2 * 1/2)]

= tan ⁻¹ [1] = π /4

Pregunta 12. cot(tan ⁻¹ a + cot ⁻¹ a)

Solución:

Sabemos, tan ⁻¹ x + cot ⁻¹ x = π /2

Por lo tanto, cot(tan ⁻¹ a + cot ⁻¹ a) = cot( π /2) =0

Pregunta 13. $tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}],|x|<1,y>0,xy<1$

Solución:

Sabemos, 2tan ^-1 x = $sin^{-1}\frac{2 x}{1+x^2}$ y 2tan ^-1 y = $cos^{-1}[\frac{1 - y^2 }{1+y^2}]$

$\therefore tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}]$

= tan( 1/2)[2( tan ⁻¹x + tan ⁻¹y) ]

= bronceado [ bronceado ⁻¹x + bronceado ⁻¹y ]

Además, tan ⁻¹x + tan ⁻¹y = $tan^{-1}\frac{x+y}{1-xy}$

Por lo tanto, tan[ tan ⁻¹x + tan ⁻¹y] = $tan[tan^{-1}\frac{x+y}{1-xy}]$

= (x + y)/(1 – xy)

Pregunta 14. Si sin(sin ⁻¹ 1/5 + cos ⁻¹ x) = 1 entonces encuentra el valor de x

Solución:

sen ⁻¹ 1/5 + cos ⁻¹ x = sen ⁻¹ 1

Sabemos, sen ⁻¹ 1 = π/2

Por lo tanto, sen ⁻¹ 1/5 + cos ⁻¹ x = π/2

sen ⁻¹ 1/5 = π/2 – cos ⁻¹ x

Ya que, sen ⁻¹ x + cos ⁻¹ x = π/2

Por tanto, π/2 – cos ⁻¹ x = sen ⁻¹ x

sen ⁻¹ 1/5 = sen ⁻¹ x

Entonces, x = 1/5

Pregunta 15. Si 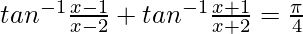$tan^{-1}\frac{x-1}{x-2} + tan^{-1}\frac{x+1}{x+2} = \frac{\pi}{4}$ , entonces encuentra el valor de x

Solución:

Sabemos, tan ⁻¹ x + tan ⁻¹ y = $tan^{-1}\frac{x+y}{1-xy}$

$tan^{-1}\frac{x-1}{x-2} + tan^{-1}\frac{x+1}{x+2} =tan^{-1}\frac{\frac{x-1}{x-2}+\frac{x+1}{x+2}}{1-\frac{x-1}{x-2}.\frac{x+1}{x+2}} = \frac{\pi}{4}$

$tan^{-1}\frac{\frac{(x-1)(x+2)+(x+1)(x-2)}{(x-2)(x+2)}}{\frac{(x-2)(x+2)-(x+1)(x-1)}{(x-2)(x+2)}} = \frac{\pi}{4}$

$tan^{-1}\frac{(x-1)(x+2)+(x+1)(x-2)}{(x-2)(x+2)-(x+1)(x-1)} = \frac{\pi}{4}$

$tan^{-1}(\frac{x^2+2x-x-2+x^2-2x+x-2}{x^2-4-x^2+1}) = \frac{\pi}{4}$

$tan^{-1}(\frac{x^2+x-2+x^2-x-2}{-3}) = \frac{\pi}{4}$

$tan^{-1}(\frac{2x^2-4}{-3}) = \frac{\pi}{4}$

$\frac{2x^2-4}{-3} = tan(\frac{\pi}{4})$

$\frac{2x^2-4}{-3} = 1$

2x ² – 4 = -3

2x ² – 4 + 3 = 0

2x ² – 1 = 0

× ² = 1/2

x = 1/√2, -1/√2

Encuentra los valores de cada una de las expresiones en los ejercicios 16 a 18.

Pregunta 16. sen ^{− 1} (sen2π/3)

Solución:

Sabemos que sen ⁻¹ ( senθ ) = θ cuando θ ∈ [- π/2, π/2], pero $\frac{2 \pi}{3} > \frac{\pi}{2}$

Entonces, sin ^{− 1} (sin2π/3) se puede escribir como $sin^{-1}[sin(\pi-\frac{2\pi}{3})]$

sin ^{− 1} (sinπ/3) aquí $\frac{-\pi}{2}<\frac{\pi}{3}<\frac{\pi}{2}$

Por lo tanto, sen ^{− 1} (senπ/3) = π/3

Pregunta 17. tan ⁻¹ (tan3π/4)

Solución:

Sabemos que tan ⁻¹ (tanθ) = θ cuando $\theta \epsilon(\frac{-\pi}{2},\frac{\pi}{2})$ pero $\frac{3 \pi}{4} > \frac{\pi}{2}$

Entonces, tan ⁻¹ (tan3π/4) se puede escribir como tan ⁻¹ (-tan(-3π/4))

= bronceado ⁻¹ [- bronceado ( π – π/4 )]

= bronceado ⁻¹ [- bronceado ( π/4 )]

= – bronceado ⁻¹ [ bronceado ( π/4 )]

= – π/4 donde $\frac{-\pi}{4} \epsilon(\frac{-\pi}{2},\frac{\pi}{2})$

Pregunta 18. 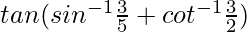$tan(sin^{-1}\frac{3}{5} + cot^{-1}\frac{3}{2})$

Solución:

Supongamos $sin^{-1}\frac{3}{5}$ = x , entonces senx = 3/5

Sabemos, $cosx = \sqrt{1-sin^2x}$

$\therefore cosx = \sqrt{1-(\frac{3}{5})^2}$

$cosx = \sqrt{1-\frac{9}{25}}$

$cosx = \sqrt{\frac{25-9}{25}}$

$cosx = \sqrt{\frac{16}{25}}$

cos x = 4/5

Sabemos, $tanx = \frac{sinx}{cosx}$

Asi que, $tanx = \frac{\frac{3}{5}}{\frac{4}{5}}$

tanx = 3/4

También, $tan^{-1}\frac{1}{x} = cot^{-1}x$

Por eso, $tan(sin^{-1}\frac{3}{5} + cot^{-1}\frac{3}{2}) = tan(tan^{-1}\frac{3}{4}+tan^{-1}\frac{2}{3})$

bronceado ^-1 x + bronceado ^-1 y = $tan^{-1}\frac{x+y}{1-xy}$

Asi que, $tan(tan^{-1}\frac{3}{4}+tan^{-1}\frac{2}{3}) = tan(tan^{-1}\frac {\frac{3}{4}+\frac{2}{3}}{1-\frac{3}{4}.\frac{2}{3}})$

$= tan(tan^{-1}\frac{\frac{9+8}{12}}{\frac{12-6}{12}})$

$= tan(tan^{-1}\frac{17}{6})$

= 17/6

Pregunta 19. cos ⁻¹ (cos7π/6) es igual a

(i) 7π/6 (ii) 5π/6 (iii)π/3 (iv)π/6

Solución:

Sabemos que cos ⁻¹ (cosθ) = θ, θ ∈ [0, π]

cos ⁻¹ (cosθ) = θ, θ ∈ [0, π]

Aquí, 7π/6 > π

Entonces, cos ⁻¹ (cos7π/6) se puede escribir como cos ⁻¹ (cos(-7π/6))

= cos ⁻¹ [ cos (2 π – 7 π/6 )] [cos(2π + θ) = θ]

= cos ⁻¹ [ cos (5 π/6 )] donde 5π/6 ∈ [0, π]

Por lo tanto, cos ⁻¹ [ cos (5 π/6 )] = 5 π/6

Pregunta 20. $sin[\frac{\pi}{3} - sin^{-1}(-\frac{1}{2} )]$

(i) 1/2 (ii) 1/3 (iii) 1/4 (iv) 1

Solución:

Supongamos sen ^-1 (-1/2)= x, entonces senx = -1/2

Por lo tanto, x = -π/6

Por tanto, sen[π/3 – (-π/6)]

= sen[π/3 + (π/6)]

= pecado[3π/6]

= pecado[π/2]

= 1

Pregunta 21. 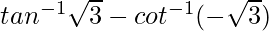$tan^{-1}\sqrt{3} - cot^{-1}(-\sqrt{3})$ es igual a

(i) π (ii) -π/2 (iii)0 (iv)2√3

Solución:

Sabemos, cot(−x) = −cotx

Por lo tanto, tan ^-1 3 – cot ^-1 (-3) = tan ^-1 3 – [-cot ^-1 (3)]

= bronceado ^-1 3 + cuna ^-1 3

Ya que, tan ^-1 x + cot ^-1 x = π/2

bronceado ^-1 3 + cuna ^-1 3 = -π/2

Publicación traducida automáticamente

Artículo escrito por pritishnagpal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 2 Funciones trigonométricas inversas – Ejercicio 2.2 | conjunto 2

Capítulo 2 Funciones trigonométricas inversas – Ejercicio 2.2 | Serie 1

Encuentre los valores de cada uno de los siguientes:

Pregunta 11. tan ⁻¹ [2cos(2sen ⁻¹ 1/2)]

Pregunta 12. cot(tan ⁻¹ a + cot ⁻¹ a)

Pregunta 13. $tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}],|x|<1,y>0,xy<1$

Pregunta 14. Si sin(sin ⁻¹ 1/5 + cos ⁻¹ x) = 1 entonces encuentra el valor de x

Pregunta 15. Si $tan^{-1}\frac{x-1}{x-2} + tan^{-1}\frac{x+1}{x+2} = \frac{\pi}{4}$ , entonces encuentra el valor de x

Encuentra los valores de cada una de las expresiones en los ejercicios 16 a 18.

Pregunta 16. sen ^{− 1} (sen2π/3)

Pregunta 17. tan ⁻¹ (tan3π/4)

Pregunta 18. $tan(sin^{-1}\frac{3}{5} + cot^{-1}\frac{3}{2})$

Pregunta 19. cos ⁻¹ (cos7π/6) es igual a

(i) 7π/6 (ii) 5π/6 (iii)π/3 (iv)π/6

Pregunta 20. $sin[\frac{\pi}{3} - sin^{-1}(-\frac{1}{2} )]$

(i) 1/2 (ii) 1/3 (iii) 1/4 (iv) 1

Pregunta 21. $tan^{-1}\sqrt{3} - cot^{-1}(-\sqrt{3})$ es igual a

(i) π (ii) -π/2 (iii)0 (iv)2√3

Deja una respuesta Cancelar la respuesta

Capítulo 2 Funciones trigonométricas inversas – Ejercicio 2.2 | Serie 1

Encuentre los valores de cada uno de los siguientes:

Pregunta 11. tan −1 [2cos(2sen −1 1/2​)]

Pregunta 12. cot(tan −1 a + cot −1 a)

Pregunta 13.

Pregunta 14. Si sin(sin −1 1/5​ + cos −1 x) = 1 entonces encuentra el valor de x

Pregunta 15. Si , entonces encuentra el valor de x

Encuentra los valores de cada una de las expresiones en los ejercicios 16 a 18.

Pregunta 16. sen − 1 (sen2π/3​)

Pregunta 17. tan −1 (tan3π/4​)

Pregunta 18.

Pregunta 19. cos −1 (cos7π/6​) es igual a

(i) 7π/6 (ii) 5π/6 (iii)π/3 (iv)π/6

Pregunta 20.

(i) 1/2 (ii) 1/3 (iii) 1/4 (iv) 1

Pregunta 21. es igual a

(i) π (ii) -π/2 (iii)0 (iv)2√3

Deja una respuesta Cancelar la respuesta

Pregunta 11. tan ⁻¹ [2cos(2sen ⁻¹ 1/2)]

Pregunta 12. cot(tan ⁻¹ a + cot ⁻¹ a)

Pregunta 13. $tan\frac{1}{2}[sin^{-1}\frac{2x}{1+x^2}+cos^{-1}\frac{1-y^2}{1+y^2}],|x|<1,y>0,xy<1$

Pregunta 14. Si sin(sin ⁻¹ 1/5 + cos ⁻¹ x) = 1 entonces encuentra el valor de x

Pregunta 15. Si $tan^{-1}\frac{x-1}{x-2} + tan^{-1}\frac{x+1}{x+2} = \frac{\pi}{4}$ , entonces encuentra el valor de x

Pregunta 16. sen ^{− 1} (sen2π/3)

Pregunta 17. tan ⁻¹ (tan3π/4)

Pregunta 18. $tan(sin^{-1}\frac{3}{5} + cot^{-1}\frac{3}{2})$

Pregunta 19. cos ⁻¹ (cos7π/6) es igual a

Pregunta 20. $sin[\frac{\pi}{3} - sin^{-1}(-\frac{1}{2} )]$

Pregunta 21. $tan^{-1}\sqrt{3} - cot^{-1}(-\sqrt{3})$ es igual a