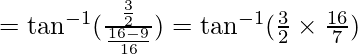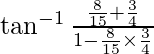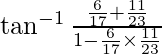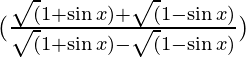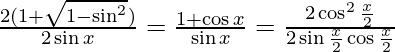Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 2 Funciones trigonométricas inversas – Ejercicio misceláneo en el Capítulo 2 | Serie 1

Posted on by Rudeus Greyrat

Pregunta 1. Encuentra el valor de 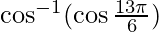{\cos }^{-1}(\cos \frac {13\pi} {6})

Solución: 

Lo sabemos \cos^{-1} (\cos x)=x  

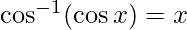
Aquí, \frac {13\pi} {6} \notin [0,\pi].

Ahora,  {\cos }^{-1}(\cos \frac {13\pi} {6})  se puede escribir como:

{\cos }^{-1}(\cos \frac {13\pi} {6})={\cos }^{-1}[\cos( 2\pi+\frac {\pi} {6})] , dónde \frac{\pi} {6} \in [0,\pi].

Por lo tanto, el valor de  {\cos }^{-1}(\cos \frac {13\pi} {6})  = π/ 6

Pregunta 2. Encuentra el valor de 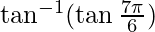\tan^{-1}(\tan \frac {7\pi}{6})

Solución: 

Lo sabemos \tan^{-1} (\tan x)=x

Aquí, \frac {7\pi}{6} \notin(\frac{-\pi}{2},\frac{\pi}{2})

Ahora,  \tan^{-1}(\tan \frac {7\pi}{6})  se puede escribir como:

\tan^{-1}(\tan \frac {7\pi}{6})=\tan^{-1}[\tan( 2\pi -\frac {5\pi}{6})]       -[\tan(2\pi-x)=-\tan x]

\tan^{-1}[-\tan(\frac {5\pi}{6}) ]=\tan^{-1}[\tan(-\frac {5\pi}{6})]

=\tan^{-1}[\tan(\pi-\frac {5\pi}{6})]=\tan^{-1}[\tan( \frac {\pi}{6})],  dónde \frac{\pi}{6} \in (\frac{-\pi}{2},\frac{\pi}{2})

Por lo tanto, el valor de  \tan^{-1}(\tan\frac{7\pi}{6})  = π/ 6

Pregunta 3. Prueba 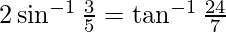2\sin^{-1} \frac{3}{5}=\tan^{-1} \frac{24}{7}

Solución: 

Sea   -(1) \sin^{-1} \frac{3}{5}=x        

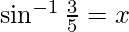
sen x = 3/5

Entonces, \cos x = \sqrt{1-(\frac{3}{5})^2 } = 4/5

tan x = 3/4

Por eso, x=\tan^{-1} \frac{3}{4}

Ahora pon el valor de x de la ecuación (1), obtenemos

\sin^{-1} \frac{3}{5}=\tan^{-1} \frac{3}{4}

Ahora tenemos

LHS = 2 \sin^{-1} \frac{3}{5}=2 \tan^{-1} \frac{3}{4}

=  \tan^{-1}(\frac{2 \times \frac{3}{4}}{1-(\frac{3}{4})^{2}})                 –[2\tan^{-1} x=\tan^{-1} \frac{2x}{1-x^2}]

= \tan^{-1}(\frac{ \frac{3}{2}}{\frac{16-9}{16}})=\tan^{-1} (\frac{3}{2} \times \frac{16}{7})

=\tan^{-1} \frac{24}{7}

Por lo tanto, probado.

Pregunta 4. Demostrar 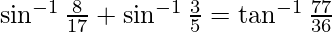\sin^{-1} \frac{8}{17}+\sin^{-1} \frac{3}{5}=\tan^{-1} \frac{77}{36}

Solución: 

Dejar \sin^{-1} \frac{8}{17}=x  

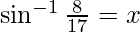
Entonces sen x = 8/17 

 porque x = \sqrt{1-(\frac{8}{17})^2}=\sqrt \frac{225}{289}  = 15/17

Por lo tanto, \tan x=\frac{8}{15}\implies x=\tan^{-1}\frac{8}{15}

\sin^{-1} \frac{8}{17}=\tan^{-1} \frac{8}{17}          -(1)

Ahora deja \sin^{-1} \frac{3}{5}=y

Entonces, sen y = 3/5 

\cos y=\sqrt{1- (\frac{3}{5})^2}=\sqrt{ (\frac{16}{25})}  = 4/5

\therefore \tan y =\frac{3}{4} \implies y=\tan^{-1} \frac{3}{4}

\therefore \sin^{-1} \frac{3}{5}=\tan^{-1} \frac{3}{4}      -(2)

Ahora tenemos:

LHS=\sin^{-1} \frac{8}{17}+\sin^{-1} \frac{3}{5}

 De la ecuación (1) y (2), obtenemos

= \tan^{-1} \frac{8}{15}+\tan^{-1} \frac{3}{4}                          

= \tan^{-1} \frac{{\frac{8}{15}+ \frac{3}{4}} }{1-{\frac{8}{15}\times \frac{3}{4}}}

=  \tan^{-1}(\frac{32+45}{60-24})                                  –[\tan^{-1} x + \tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]

= \tan^{-1} \frac{77}{36}

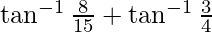
Por lo tanto probado

Pregunta 5. Demostrar 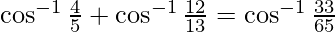\cos^{-1}\frac{4}{5}+\cos^{-1}\frac{12}{13}=\cos^{-1}\frac{33}{65}

Solución: 

Dejar \cos^{-1}\frac{4}{5}= x

Entonces, cos x = 4/5

\sin x = \sqrt {1- (\frac{4}{5})^{2}}  = 3/5

\therefore \tan x =\frac{3}{4} \implies x=\tan^{-1} \frac{3}{4}

\therefore \cos^{-1} \frac{4}{5}=\tan^{-1} \frac{3}{4}         -(1)

Ahora deja \cos^{-1} \frac{12}{13}=x

Entonces, cos y = 3/4 

\sin^{-1} y=\frac{5}{13}

\therefore\tan y= \frac{5}{12} \implies y=\tan^{-1} \frac{5}{12}

\therefore \cos ^{-1} \frac{12}{13}=\tan^{-1} \frac{5}{12}             -(2)

Dejar \cos^{-1} \frac{33}{65}=z  

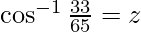
Entonces, cos z = 33/65

sen z = 56/65 

\therefore \tan z = \frac{56}{65} \implies z= tan^{-1}\frac{56}{33}

\therefore \cos^{-1} \frac{33}{65}= \tan^{-1} \frac{56}{33}     -(3)

Ahora, probaremos que: 

LHS =\cos^{-1} \frac{3}{5}\cos^{-1} \frac{12}{13}

De la ecuación (1) y la ecuación (2)

= \tan^{-1} \frac{3}{4}+\tan^{-1} \frac{5}{12}                                                                  

=  \tan^{-1} \frac{{\frac{3}{4}+ \frac{5}{12}} }{1-{\frac{3}{4}\times \frac{5}{12}}}          –[\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]

= \tan^{-1} \frac{36+20}{48-15}

= \tan^{-1} \frac{56}{33}

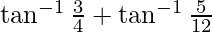
Usando la ecuación (3)

= \tan^{-1} \frac{56}{33}                                                                                                   

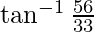
Por lo tanto probado

Pregunta 6. Demostrar 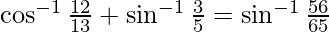\cos^{-1} \frac{12}{13}+\sin^{-1} \frac{3}{5}=\sin^{-1} \frac{56}{65}

Solución: 

Dejar \sin^{-1} \frac{3}{5}=x   

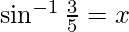
Entonces , sen x = 3/5 

\cos x =\sqrt{1- (\frac{3}{5})^{2}}=\sqrt \frac{16}{25}  = 4/5

\therefore \tan x = \frac{3}{4} \implies x= \tan^{-1} \frac{3}{4}

\therefore \sin^{-1} \frac{3}{5}= \tan^{-1} \frac{3}{4}            -(1)

Ahora deja \cos^{-1} \frac{12}{13}=y   

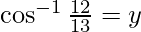
Entonces, cos y = 12/13 y sen y = 5/13

\therefore \tan y = \frac{5}{12} \implies y= \tan^{-1} \frac{5}{12}

\therefore \cos^{-1} \frac{12}{13}= \tan^{-1} \frac{5}{12}         -(2)                                                             

Dejar \sin^{-1} \frac{56}{65}=z

Entonces, sen z = 56/65 y cos z = 33/65

\therefore \tan z = \frac{56}{33} \implies z=\tan ^{-1} \frac{56}{33}

\therefore \sin^{-1} \frac{56}{65}= \tan^{-1} \frac{56}{33}            -(3)

Ahora tenemos:

IZQ=\cos^{-1} \frac{12}{13}+ \sin^{-1} \frac{3}{5}

De la ecuación (1) y la ecuación (2)

=\tan^{-1} \frac{5}{12}+\tan^{-1} \frac{3}{4}                                                                            

=  \tan^{-1} \frac{{\frac{5}{12}+ \frac{3}{4}} }{1-{\frac{5}{12}\times \frac{3}{4}}}                –[\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]

= \tan^{-1} \frac{20+36}{48-15}

= \tan^{-1} \frac{56}{33}

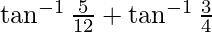
De la ecuación (3)

= \sin^{-1} \frac{56}{65}     

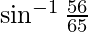
Por lo tanto probado                                                                                                           

Pregunta 7. Demostrar 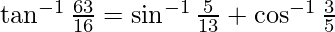\tan^{-1} \frac{63}{16}= \sin^{-1} \frac{5}{13}+\cos^{-1} \frac{3}{5}

Solución:

Dejar \sin^{-1} \frac{5}{13}=x    

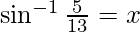
Entonces, sen x = 5/13 y cos x = 12/13.

\tan^{-1} \frac{7+5}{35-1}+\tan^{-1} \frac{8+3}{24-1}

\therefore \tan x= \frac{5}{12} \to x= \tan^{-1} \frac{5}{12}

\therefore \sin^{-1} \frac{5}{13}= \tan^{-1} \frac{5}{12}                    -(1)

Dejar \cos^{-1} \frac{3}{5}=y      

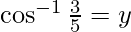
Entonces, cos y = 3/5 y sen y = 4/5

\therefore \tan y= \frac{4}{3} \implies y= \tan^{-1}\frac{4}{3}

\therefore \cos ^{-1}\frac{3}{5}=\tan^{-1} \frac{4}{3}                 -(2)

De la ecuación (1) y (2), tenemos

lado derecho=\sin^{-1} \frac{5}{13}+\cos^{-1} \frac{3}{5}

=\tan^{-1} \frac{5}{12}+\tan^{-1} \frac{4}{3}

=  \tan^{-1} \frac{{\frac{5}{12}+ \frac{4}{3}} }{1-{\frac{5}{12}\times \frac{4}{3}}}           –[\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]

=\tan^{-1} \frac{15+48}{36-20}

=\tan^{-1} \frac{63}{16}

LHS = RHS

Por lo tanto probado

Pregunta 8. Demostrar 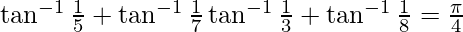\tan^{-1} \frac{1}{5}+\tan^{-1} \frac{1}{7}\tan^{-1} \frac{1}{3}+\tan^{-1} \frac{1}{8}=\frac{\pi}{4}

Solución:

LHS=\tan^{-1} \frac{1}{5}+\tan^{-1} \frac{1}{7}\tan^{-1} \frac{1}{3}+\tan^{-1} \frac{1}{8}

=  \tan^{-1} \frac{{\frac{1}{5}+ \frac{1}{7}} }{1-{\frac{1}{5}\times \frac{1}{7}}} +\tan^{-1} \frac{{\frac{1}{3}+ \frac{1}{8}} }{1-{\frac{1}{3}\times \frac{1}{8}}}      –[\tan^{-1} x +\tan^{-1} y=\tan^{-1} \frac{x+y}{1-xy}]

= \tan^{-1} \frac{7+5}{35-1}+\tan^{-1} \frac{8+3}{24-1}

= \tan^{-1} \frac{12}{34}+\tan^{-1} \frac{11}{23}

= \tan^{-1} \frac{6}{17}+\tan^{-1} \frac{11}{23}

= \tan^{-1} \frac{{\frac{6}{17}+ \frac{11}{23}} }{1-{\frac{6}{17}\times \frac{11}{23}}}

= \tan^{-1} \frac{138 + 187}{391-66}

= \tan^{-1} \frac{325}{325}=\tan^{-1} 1

= π/4 

LHS = RHS

Por lo tanto probado

Pregunta 9. Demostrar \tan^{-1} \sqrt x= \frac{1}{2} \cos^{-1} (\frac{1-x}{1+x}),x\in[0,1]

Solución:

Sea x = tan 2 θ

Después,\sqrt x=\tan \theta \implies\theta=\tan^{-1} \sqrt x.

\therefore \frac{1-x}{1+x}+\frac{1-\tan^{2}\theta}{1+\tan^{2}\theta}=\cos 2\theta

Ahora tenemos

lado derecho = \frac{1}{2} \cos ^{-1}(\frac{1-x}{1+x})= \frac{1}{2} \cos ^{-1} (\cos 2 \theta)=\frac{1}{2} \times 2 \theta=\theta=\tan^{-1}\sqrt x

LHS = RHS

Por lo tanto probado

Pregunta 10. Demostrar 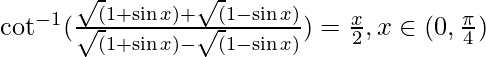\cot^{-1} (\frac{\sqrt ({1+ \sin x}) + \sqrt ({1-\sin x})} {\sqrt ({1+ \sin x})-\sqrt ({1- \sin x})})=\frac{x}{2},x\in(0,\frac{\pi}{4})

Solución:

Considerar (\frac{\sqrt ({1+ \sin x}) + \sqrt ({1-\sin x})} {\sqrt ({1+ \sin x})-\sqrt ({1- \sin x})})

Al racionalizar

= \frac{(\sqrt ({1+ \sin x}) + \sqrt ({1-\sin x}))^{2}}{(\sqrt{ ({1+ \sin x})}-\sqrt({1- \sin x}))^{2}}                          

= \frac{( {1+ \sin x)} + {(1-\sin x)} + 2 \sqrt{(1+\sin x)(1-\sin x)}}{{ {1+ \sin x}}-{1+\sin x}}

=\frac{2(1+\sqrt{1-\sin^{2}})}{2\sin x}=\frac{1+\cos x}{\sin x}=\frac{2\cos ^{2}\frac{x}{2}}{2\sin \frac{x}{2}\cos\frac{x}{2}}

= \cot \frac{x}{2}

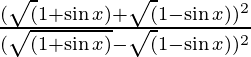
LHS =  \cot^{-1} (\frac{\sqrt ({1+ \sin x}) + \sqrt ({1-\sin x})} {\sqrt ({1+ \sin x})-\sqrt ({1- \sin x})})={\cot}^{-1}({\cot( \frac x 2)}) = x/2

LHS = RHS

Por lo tanto probado

Capítulo 2 Funciones trigonométricas inversas – Ejercicio misceláneo en el Capítulo 2 | conjunto 2

Publicación traducida automáticamente

Artículo escrito por simardeep032002 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *