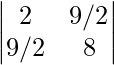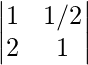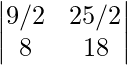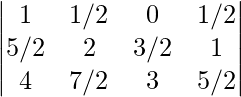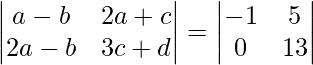Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 3 Arrays – Ejercicio 3.1

Pregunta 1. En la array A = 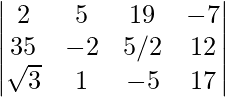$\begin{vmatrix} 2&5&19&-7\\ 35&-2&5/2&12\\ \sqrt{3}&1&-5&17\\ \end{vmatrix}$ , escribe:

(i) El orden de la array

Solución:

Podemos ver que la array contiene 3 filas y 4 columnas Entonces, el orden de esta array es 3×4

(ii) El número de elementos

Solución:

Sabemos que el número de elementos en la array = producto del número de filas y el número de columnas en la array Entonces, el número de elementos = 3 x 4 =12.

(iii) Escriba los elementos a ₁₃ , a ₂₁ , a ₃₃ , a ₂₄ , a ₂₃

Solución:

a ₁₃ = Elemento en primera fila y tercera columna, es decir, 19

a ₂₁ = Elemento en la segunda fila y primera columna, es decir, 35

a ₃₃ = Elemento en tercera fila y tercera columna, es decir, -5

a ₂₄ = Elemento en la segunda fila y cuarta columna, es decir, 12

a ₂₃ = Elemento en la segunda fila y tercera columna, es decir, 5/2

Pregunta 2. Si una array tiene 24 elementos, ¿cuáles son los posibles órdenes que puede tener? ¿Y si tiene 13 elementos?

Solución:

Sabemos que el número de elementos en la array es el producto del número

de filas y número de columnas en la array.

Si la array tiene un orden de mxn, entonces el número de elementos es mn en esa array.

Entonces tenemos que encontrar los pares ordenados de números naturales cuyo producto es 24.

Los pares ordenados son: (1, 24), (24, 1), (2, 12), (12, 2), (3, 8), (8, 3), (4, 6), (6, 4)

Por lo tanto, los órdenes posibles son: 1 × 24, 24 × 1, 2 × 12, 12 × 2, 3 × 8, 8 × 3, 4 × 6 y 6 × 4

Si la array tiene 13 elementos, los pares ordenados serán (1, 13) y (13, 1)

Por lo tanto, los órdenes posibles son: 1×13 y 13×1

Pregunta 3. Si una array tiene 18 elementos, ¿cuáles son los posibles órdenes que puede tener? ¿Qué pasa si tiene 5 elementos?

Solución:

Sabemos que el número de elementos en la array es el producto del número

de filas y número de columnas en la array.

Si la array tiene un orden de mxn, entonces el número de elementos es mn en esa array.

Entonces tenemos que encontrar los pares ordenados de números naturales cuyo producto es 18.

Los pares ordenados son: (1, 18), (18, 1), (2, 9), (9, 2), (3, 6) y (6, 3)

Por lo tanto, los órdenes posibles son: 1 × 18, 18 × 1, 2 × 9, 9 × 2, 3 × 6 y 6 × 3

Si la array tiene 5 elementos, los pares ordenados serán (1, 5) y (5, 1)

Por lo tanto, los órdenes posibles son: 1×5 y 5×1

Pregunta 4. Construya una array de 2×2, A = [a _ij ] cuyos elementos estén dados por:

( i) un _ij = (i + j) ^2/2

Solución:

Elementos en esta array de 2×2 = a ₁₁ , a ₁₂ ,a ₂₁ ,a ₂₂

a ₁₁ => i = 1 y j = 1 => (1 + 1) ^2/2 = 4/2 = 2

a ₁₂ => i = 1 y j = 2 => (1 + 2) ^2/2 = 9/2

a ₂₁ => i = 2 y j = 1 => (2 + 1) ^2/2 = 9/2

a ₂₂ => i = 2 y j = 2 =>(2 + 2) ² /2 = 16/2 = 8

La array resultante es:

$\begin{vmatrix} 2&9/2\\ 9/2&8\\ \end{vmatrix}$

(ii) aij ₌ i/j

Solución:

Elementos en esta array de 2×2 = a ₁₁ , a ₁₂ ,a ₂₁ ,a ₂₂

a ₁₁ => i = 1 y j = 1 = 1/1 = 1

a ₁₂ => i = 1 y j = 2 = 1/2

a ₂₁ => i = 2 y j = 1 = 2/1 = 2

a ₂₂ => i = 2 y j = 2 = 2/2 = 1

La array resultante es:

$\begin{vmatrix} 1&1/2\\ 2&1\\ \end{vmatrix}$

(iii) aij ₌ (i + 2j ) ^2/2

Solución:

Elementos en esta array de 2×2 = a ₁₁ , a ₁₂ , a ₂₁ , a ₂₂

a ₁₁ => i = 1 y j = 1 => (1 + 2 x 1) ^2/2 = 9/2

a ₁₂ => i = 1 y j = 2 => (1 + 2 x 2) ^2/2 = 25/2

a ₂₁ => i = 2 y j = 1 =>(2 + 2 x 1) ² /2 = 16/2 = 8

a ₂₂ => i = 2 y j = 2 =>(2 + 2 x 2) ² /2 = 36/2 = 18

La array resultante es:

$\begin{vmatrix} 9/2&25/2\\ 8&18\\ \end{vmatrix}$

Pregunta 5. Construye una array de 3×4, cuyos elementos están dados por:

(i) aij ₌ 1/2 {|-3i + j|}

Solución:

Los elementos de esta array de 3 x 4 son ₁₁ , ₁₂ , ₁₃ , ₁₄ , ₂₁ , ₂₂ , ₂₃ , ₂₄_,₃₁ , ₃₂ , 33 , ₃₄

a ₁₁ => i = 1 y j = 1 => 1/2 (|-3 x 1 + 1|) = 1

a ₁₂ => i = 1 y j = 2 => 1/2 (|-3 x 1 + 2|) = 1/2

a ₁₃ => i = 1 y j = 3 => 1/2 (|-3 x 1 + 3) = 0

a ₁₄ => i = 1 y j = 4 => 1/2 (|-3 x 1 + 4|) = 1/2

a ₂₁ => i = 2 y j = 1 => 1/2 (|-3 x 2 + 1|) = 5/2

a ₂₂ => i = 2 y j = 2 => 1/2 (|-3 x 2 + 2|) = 2

a ₂₃ => i = 2 y j = 3 => 1/2 (|-3 x 2 + 3|) = 3/2

a ₂₄ => i = 2 y j = 4 => 1/2 (|-3 x 2 + 4|) = 1

a ₃₁ => i = 3 y j = 1 => 1/2 (|-3 x 3 + 1|) = 4

a ₃₂ => i = 3 y j = 2 => 1/2 (|-3 x 3 + 2|) = 7/2

a ₃₃ => i = 3 y j = 3 => 1/2 (|-3 x 3 + 3|) = 3

a ₃₄ => i = 3 y j = 4 => 1/2 (|-3 x 3 + 4|) = 5/2

La array resultante es:

$\begin{vmatrix} 1&1/2&0&1/2\\ 5/2&2&3/2&1\\ 4&7/2&3&5/2\\ \end{vmatrix}$

(ii) un _ij = 2i – j

Solución:

Los elementos de esta array de 3 x 4 son ₁₁ , ₁₂ , ₁₃ , ₁₄ , ₂₁ , ₂₂ , ₂₃ , ₂₄_,₃₁ , ₃₂ , 33 , ₃₄

Asi que,

a ₁₁ => i = 1 y j = 1 => 2 x 1 – 1 = 1

a ₁₂ => i = 1 y j = 2 => 2 x 1 – 2 = 0

a ₁₃ => i = 1 y j = 3 => 2 x 1 – 3 = -1

a ₁₄ => i = 1 y j = 4 => 2 x 1 – 4 = -2

a ₂₁ => i = 2 y j = 1 => 2 x 2 – 1 = 3

a ₂₂ => i = 2 y j = 2 => 2 x 2 – 2 = 2

a ₂₃ => i = 2 y j = 3 => 2 x 2 – 3 = 1

a ₂₄ => i = 2 y j = 4 => 2 x 2 – 4 = 0

a ₃₁ => i = 3 y j = 1 => 2 x 3 – 1 = 5

a ₃₂ => i = 3 y j = 2 => 2 x 3 – 2 = 4

a ₃₃ => i = 3 y j = 3 => 2 x 3 – 3 = 3

a ₃₄ => i = 3 y j = 4 => 2 x 3 – 4 = 2

La array resultante es: $\begin{vmatrix} 1&0&-1&-2\\ 3&2&1&0\\ 5&4&3&2\\ \end{vmatrix}$

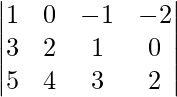
Pregunta 6. Encuentra los valores de x, y y z a partir de las siguientes ecuaciones:

(i) 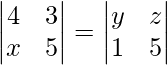$\begin{vmatrix} 4&3\\ x&5\\ \end{vmatrix} = \begin{vmatrix} y&z\\ 1&5\\ \end{vmatrix}$

Solución:

Podemos comparar o igualar ambas arrays porque ambas son iguales

Entonces al igualar ambas arrays obtenemos

x = 1; y = 4; z = 3

(ii) 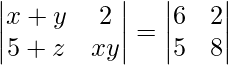$\begin{vmatrix} x+y&2\\ 5+z&xy\\ \end{vmatrix} = \begin{vmatrix} 6&2\\ 5&8\\ \end{vmatrix}$

Solución:

Podemos comparar o igualar ambas arrays porque ambas son iguales

Entonces, al igualar ambas arrays. obtenemos

x + y = 6 -(1)

5 + z = 5 -(2)

xy = 8 -(3)

Ahora, podemos resolver estas ecuaciones.

z = 0 de la ecuación (2)

x = 6 – y -(4)

Ahora poniendo el valor de x de eq(4) en eq(3)

(6 – y)(y) = 8

6y – y2 ⁼ 8

y ² – 6y + 8 = 0 -(5)

Ahora tenemos que factorizar esta ecuación.

(y – 4)(y – 2) = 0

ya sea y – 4 = 0 o y – 2 = 0

entonces, y = 2 o y = 4

Ponga estos valores en la ecuación (4) obtenemos

x = 4 y x = 2

Por lo tanto, el valor de x = 2 , y = 4 , z = 0

(iii) 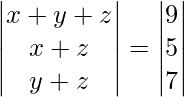$\begin{vmatrix} x+y+z\\ x+z\\ y+z\\ \end{vmatrix} = \begin{vmatrix} 9\\ 5\\ 7\\ \end{vmatrix}$

Solución:

Podemos comparar o igualar ambas arrays porque ambas son iguales

Entonces, al igualar ambas arrays, obtenemos

x + y + z = 9 -(1)

x + z = 5 -(2)

y + z = 7 -(3)

Si ponemos el valor de eq(2) en eq(1)

obtenemos, 5 + y = 9

y = 4

Al poner el valor de y en la ecuación (3)

4 + z = 7

z = 3

Al poner el valor de z en la ecuación (2)

x + 3 = 5

x = 2

Entonces, el valor de x = 2; y = 4; z = 3

Pregunta 7. Encuentra el valor de a, b, c y d de la ecuación:

$\begin{vmatrix} a-b&2a+c\\ 2a-b&3c+d\\ \end{vmatrix} = \begin{vmatrix} -1&5\\ 0&13\\ \end{vmatrix}$

Solución:

Podemos comparar o igualar ambas arrays porque ambas son iguales

Entonces, al igualar ambas arrays, obtenemos

a – b = -1 -(1)

2a – b = 0 -(2)

2a + c= 5 -(3)

3c + d = 13 -(4)

Al resolver la ecuación (1) y la ecuación (2) obtenemos

un = 1

Al poner a = 1 en la ecuación (3) obtenemos

c = 3

Al poner a = 1 en la ecuación (2) obtenemos

segundo = 2

Al poner c = 3 en la ecuación (4) obtenemos

re = 4

Entonces, el valor de a = 1; b = 2; c = 3; re = 4

Pregunta 8. A = [a _ij ] _mxn es una array cuadrada, si

(A) m < n (B) m > n (C) m = n (D) Ninguno de estos

Solución:

Esta será una array cuadrada si el número de filas = número de columnas

Entonces, m = n es la opción correcta.

Por lo tanto, la opción de respuesta es C.

Pregunta 9. ¿Cuáles de los valores dados de x e y hacen que el siguiente par de arrays sea igual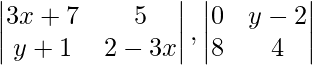 $\begin{vmatrix} 3x+7&5\\ y+1&2-3x\\ \end{vmatrix}, \begin{vmatrix} 0&y-2\\ 8&4\\ \end{vmatrix}$

(A) x = -1/3, y = 7 (B) No es posible encontrar (C) y = 7, x = -2/3 (D) x = -1/3, y = -2/3

Solución:

Podemos comparar o igualar ambas arrays porque ambas son iguales

Así que al igualar ambas arrays obtenemos;

3x + 7 = 0 -(1)

y + 1 = 8 -(2)

2 – 3x = 4 -(3)

y – 2 = 5 -(4)

De eq(2) y eq(4) obtenemos el mismo valor de y, es decir, y=7

pero al resolver la ecuación (1) obtenemos el valor de x = -7/3 y al resolver la ecuación (3) obtenemos el valor de x = -2/3

Ambos valores de x son diferentes para el valor de y. Por lo tanto, no es posible encontrar.

Por lo tanto, la opción correcta es B

Pregunta 10. El número de todas las arrays posibles de orden 3 × 3 con cada entrada 0 o 1 es:

(A) 27 (B) 18 (C) 81 (D) 512

Solución:

Sabemos que el número de elementos en una array de orden mxn es mn.

Entonces, el número de elementos en una array de 3 x 3 es 9.

Para cada elemento tenemos dos opciones, 0 o 1

Entonces, número total de arrays posibles de orden 3 x 3 con cada entrada 0 o 1 = 2 ⁹ = 512

La opción correcta es D

Publicación traducida automáticamente

Artículo escrito por DivyansheeVarshney y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. En la array A = , escribe:

(i) El orden de la array

(ii) El número de elementos

(iii) Escriba los elementos a 13 , a 21 , a 33 , a 24 , a 23

Pregunta 2. Si una array tiene 24 elementos, ¿cuáles son los posibles órdenes que puede tener? ¿Y si tiene 13 elementos?

Pregunta 3. Si una array tiene 18 elementos, ¿cuáles son los posibles órdenes que puede tener? ¿Qué pasa si tiene 5 elementos?

Pregunta 4. Construya una array de 2×2, A = [a ij ] cuyos elementos estén dados por:

( i) un ij = (i + j) 2/2

(ii) aij = i/j

(iii) aij = (i + 2j ) 2/2

Pregunta 5. Construye una array de 3×4, cuyos elementos están dados por:

(i) aij = 1/2 {|-3i + j|}

(ii) un ij = 2i – j

Pregunta 6. Encuentra los valores de x, y y z a partir de las siguientes ecuaciones:

(i)

(ii)

(iii)

Pregunta 7. Encuentra el valor de a, b, c y d de la ecuación:

Pregunta 8. A = [a ij ] mxn es una array cuadrada, si

(A) m < n (B) m > n (C) m = n (D) Ninguno de estos

Pregunta 9. ¿Cuáles de los valores dados de x e y hacen que el siguiente par de arrays sea igual

(A) x = -1/3, y = 7 (B) No es posible encontrar (C) y = 7, x = -2/3 (D) x = -1/3, y = -2/3

Pregunta 10. El número de todas las arrays posibles de orden 3 × 3 con cada entrada 0 o 1 es:

(A) 27 (B) 18 (C) 81 (D) 512

Deja una respuesta Cancelar la respuesta

Pregunta 1. En la array A = $\begin{vmatrix} 2&5&19&-7\\ 35&-2&5/2&12\\ \sqrt{3}&1&-5&17\\ \end{vmatrix}$ , escribe:

(iii) Escriba los elementos a ₁₃ , a ₂₁ , a ₃₃ , a ₂₄ , a ₂₃

Pregunta 4. Construya una array de 2×2, A = [a _ij ] cuyos elementos estén dados por:

( i) un _ij = (i + j) ^2/2

(ii) aij ₌ i/j

(iii) aij ₌ (i + 2j ) ^2/2

(i) aij ₌ 1/2 {|-3i + j|}

(ii) un _ij = 2i – j

(i) $\begin{vmatrix} 4&3\\ x&5\\ \end{vmatrix} = \begin{vmatrix} y&z\\ 1&5\\ \end{vmatrix}$

(ii) $\begin{vmatrix} x+y&2\\ 5+z&xy\\ \end{vmatrix} = \begin{vmatrix} 6&2\\ 5&8\\ \end{vmatrix}$

(iii) $\begin{vmatrix} x+y+z\\ x+z\\ y+z\\ \end{vmatrix} = \begin{vmatrix} 9\\ 5\\ 7\\ \end{vmatrix}$

Pregunta 8. A = [a _ij ] _mxn es una array cuadrada, si

Pregunta 9. ¿Cuáles de los valores dados de x e y hacen que el siguiente par de arrays sea igual $\begin{vmatrix} 3x+7&5\\ y+1&2-3x\\ \end{vmatrix}, \begin{vmatrix} 0&y-2\\ 8&4\\ \end{vmatrix}$