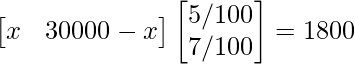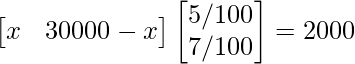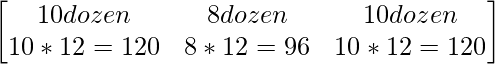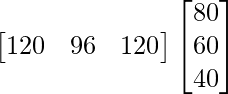Capítulo 3 Arrays – Ejercicio 3.2 | Serie 1
Pregunta 11. Si ![Rendered by QuickLaTeX.com x\left[\begin{array}{l} 2 \\ 3 \end{array}\right]+y\left[\begin{array}{c} -1 \\ 1 \end{array}\right]=\left[\begin{array}{l} 10 \\ 5 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43bb18c5c94ec6ec243b6059b04551d5_l3.png) , encuentra los valores de x e y.
, encuentra los valores de x e y.
Solución:
Dado:
Igualando las entradas correspondientes, tenemos
2x – y = 10 -(1)
3x + y = 5 -(2)
Sumando las ecuaciones (1) y (2), tenemos 5x = 15 ⇒ x = 3
Poniendo x = 3 en la ecuación (2)
9 + y = 5 ⇒ y = -4
Por lo tanto, x = 3 y y = -4
Pregunta 12. Dado ![Rendered by QuickLaTeX.com 3\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]=\left[\begin{array}{cc} x & 0 \\ -1 & 2 w \end{array}\right]+\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43d6ccb2b7ea5050cc3607f19fa50b88_l3.png) , encuentra los valores de x, y, z y w.
, encuentra los valores de x, y, z y w.
Solución:
Dado:
Igualando las entradas correspondientes, tenemos
3x = x + 4 ⇒ 2x = 4 ⇒ x = 2
y 3y = 6 + x + y
⇒ 2y = 6 + 2
⇒ 2 años = 8
⇒ y = 4
y 3z = -1 + z + w ⇒ 2z – w = – 1 -(1)
y 3w = 2w + 3 ⇒ w = 3
Poniendo w = 3 en la ecuación (i), 2z – 3 = -1
⇒ 2z = 2 ⇒ z = 1
Por lo tanto, x = 2, y = 4, z = 1, w = 3
Pregunta 13. Si ![Rendered by QuickLaTeX.com F(x)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46f434f084a2e0e8815d48f44e56e794_l3.png) , demuestre que F(x) F(y) = F(x + y).
, demuestre que F(x) F(y) = F(x + y).
Solución:
= F(x + y)
= F(x) F(y) = F(x + y)
Pregunta 14. Demuestra que
Solución:
(i) LHS =
lado derecho =
Por lo tanto, de (1) y (2), obtenemos
es decir, LHS ≠ RHS
(ii) LHS =
Multiplica ambas arrays.
RHS=
Por lo tanto,
IZQ ≠ DERECHO
es decir
Pregunta 15. Encuentra A 2 – 5A + 6I, si 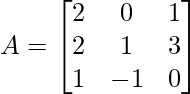
Solución:
Pregunta 16. Si 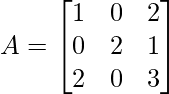 , prueba que A 3 – 6A 2 + 7A + 2I = 0
, prueba que A 3 – 6A 2 + 7A + 2I = 0
Solución:
= 0 (array cero)
= lado derecho
Por lo tanto probado
Pregunta 17. Si 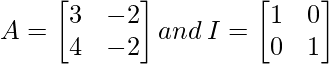 , encuentra k tal que A 2 = kA – 2I
, encuentra k tal que A 2 = kA – 2I
Solución:
Dado:
Igualando las entradas correspondientes, tenemos
3k – 2 = 1
3k = 3
k = 1
y 4k = 4
k = 1
y -4 = -2k – 2
2k = 2
k = 1
Por lo tanto, k = 1
Pregunta 18. Si 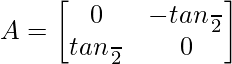 e I es la array identidad de orden 2, demostrar que I + A = (I – A)
e I es la array identidad de orden 2, demostrar que I + A = (I – A)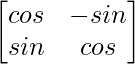
Solución:
LHS = RHS
Por lo tanto, Probado.
Pregunta 19. Un fondo fiduciario tiene ₹ 30,000 que deben invertirse en dos tipos diferentes de bonos. El primer bono paga 5% de interés anual y el segundo bono paga 7% de interés anual. Utilizando la multiplicación de arrays, determine cómo dividir ₹ 30 000 entre los dos tipos de bonos. Si el fideicomiso debe obtener un interés total anual de:
(a) 1800 rupias
(b) 2000 rupias
Solución:
Let invertido en el primer bono = Rs x
Entonces, la suma de dinero invertida en el segundo bono = ₹(30000 – x)
Se da que el primer bono paga 5% de interés anual y el segundo bono paga 7% de interés anual.
Así, para obtener un interés total anual de ₹1800, obtenemos:
⇒ 5x/100 + 7(30000 − x)/100 = 1800
⇒ 5x + 210000 -7x = 180000
⇒ 210000 -2x = 180000
⇒ 2x = 210000 – 180000
⇒ 2x = 30000
⇒ x = 15000
Por lo tanto, para obtener un interés total anual de 1800 rupias, el fondo fiduciario debe invertir 15 000 rupias en el primer bono y los 15 000 rupias restantes en el segundo bono.
Por lo tanto, la cantidad invertida en cada tipo de bonos se puede representar en forma de array con cada columna correspondiente a un tipo diferente de bono como:
X =
Por lo tanto, el interés obtenido después de un año se puede expresar en representación matricial como:
⇒ 5x/100 + 7(30000 − x)/100 = 2000
⇒ 5x + 210000 − 7x = 200000
⇒ 210000 − 2x = 200000
⇒ 2x = 210000 – 200000
⇒ 2x = 10000
⇒ x = 5000
Por lo tanto, para obtener un interés total anual de ₹ 2000, el fondo fiduciario debe invertir ₹ 5000 en el primer bono y los restantes ₹ (30 000 − 5000) = ₹ 25 000 en el segundo bono.
Pregunta 20. La librería de una escuela en particular tiene 10 docenas de libros de química, 8 docenas de libros de física, 10 docenas de libros de economía. Sus precios de venta son Rs.80, Rs.60 y Rs.40 cada uno respectivamente. Encuentre la cantidad total que recibirá la librería por vender todos los libros usando álgebra matricial.
Solución:
Sea el número de libros como array 1 × 3 = B =
Sea el precio de venta de cada libro una array de 3 × 1 S =
Por lo tanto, Monto total recibido por la venta de todos los libros = BS =
Por lo tanto, la cantidad total recibida por la venta de todos los libros = Rs 20.160
Suponga que X, Y, Z, W y P son arrays de orden 2 × n, 3 × k, 2 × p, n × 3 y p × k, respectivamente. Elige la respuesta correcta en los ejercicios 21 y 22.
Pregunta 21. Las restricciones sobre n, k y p para que se defina PY + WY son:
(A) k = 3, p = n (B) k es arbitrario, p = 2
(C) p es arbitrario, k = 3 (D) k = 2, p = 3
Solución:
Ya que, las Arrays P e Y son del orden p × k y 3 × k respectivamente.
Por lo tanto, la array PY estará definida si k = 3.
Entonces, PY será del orden p × k = p × 3.
Las arrays W e Y son del orden n × 3 y 3 × k = 3 × 3 respectivamente.
Como el número de columnas en W es igual al número de filas en Y, la array WY está bien definida y es del orden n × 3.
Las arrays PY y WY solo se pueden sumar cuando sus órdenes son iguales.
Por lo tanto, PY es del orden p × 3 y WY es del orden n × 3.
Por lo tanto, debemos tener p = n.
Por lo tanto, k = 3 y p = n son las restricciones sobre n, k y p por lo que se definirá PY + WY.
Por lo tanto, la respuesta es (A)
Pregunta 22. Si n = p, entonces el orden de la array 7X – 5Z es:
(A) p × 2 (B) 2 × n
(C) n × 3 (D) p × n
Solución:
La array X es del orden 2 × n.
Por lo tanto, la array 7X también es del mismo orden.
La array Z es de orden 2 × p = 2 × n -(∵ p = n)
Luego, Matrix 5Z también es del mismo orden.
Ahora bien, ambas arrays 7X y 5Z son del orden 2 × n.
Así, la array 7X – 5Z está bien definida y es del orden de 2 × n.
Por lo tanto, la respuesta es (B)
Publicación traducida automáticamente
Artículo escrito por kavyagupta0098 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com x\left[\begin{array}{l} 2 \\ 3 \end{array}\right]+y\left[\begin{array}{c} -1 \\ 1 \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right] \\ \Rightarrow\left[\begin{array}{c} 2 x \\ 3 x \end{array}\right]+\left[\begin{array}{c} -y \\ y \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right] \\ \Rightarrow\left[\begin{array}{c} 2 x-y \\ 3 x+y \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98d4ff2cf373ee4d5b00628ba17384c8_l3.png)
![Rendered by QuickLaTeX.com 3\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]=\left[\begin{array}{cc} x & 0 \\ -1 & 2 w \end{array}\right]+\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31f3360e6c083e580727463507f5d44b_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow\left[\begin{array}{ll} 3 x & 3 y \\ 3 z & 3 w \end{array}\right]=\left[\begin{array}{cc} x+4 & 6+x+y \\ -1+z+w & 2 w+3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11ae60b9823a2f32ed0ca6c856180197_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &\text { } F(x)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right], F(y)=\left[\begin{array}{ccc} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &F(x+y)=\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &F(x) F(y)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{array}\right] \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-04bb9df8467cc89985c725bd5905be69_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a4d00b03c154b780aceca9f218a5673_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos x \cos y-\sin x \sin y+0 & -\cos x \sin y-\sin x \cos y+0 & 0 \\ \sin x \cos y+\cos x \sin y+0 & -\sin x \sin y+\cos x \cos y+0 & 0 \\ 0 & 0 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ed8ecbefdf20a6993a583556ebd16716_l3.png)
![Rendered by QuickLaTeX.com (i) \left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1eb15d50720dc1055c4a1c8a59148792_l3.png)
![Rendered by QuickLaTeX.com \text { (ii) }\left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right] \neq\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c2ccbd5a0fa5d443c15b462a084d002_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\\ =\left[\begin{array}{ll} 5(2)-1(3) & 5(1)-1(4) \\ 6(2)+7(3) & 6(1)+7(4) \end{array}\right]\\ =\left[\begin{array}{cc} 10-3 & 5-4 \\ 12+21 & 6+28 \end{array}\right]\\ =\left[\begin{array}{cc} 7 & 1 \\ 33 & 34 \end{array}\right] \ \ \ -(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-063ca2ef15297322293644aa5cb7dc0a_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{ll} 5 & -1 \\ 6 & 7 \end{array}\right]\\ =\left[\begin{array}{ll} 2(5)+1(6) & 2(-1)+1(7) \\ 3(5)+4(6) & 3(-1)+4(7) \end{array}\right]\\ =\left[\begin{array}{cc} 10+6 & -2+7 \\ 15+24 & -3+28 \end{array}\right]\\ =\left[\begin{array}{ll} 16 & 5 \\ 39 & 25 \end{array}\right] \ \ \ -(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-065d58fda09e5f4b315411a5d4207c85_l3.png)
![Rendered by QuickLaTeX.com \text { }\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ffaa396b4e6533945db9456725a54f43_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ffc3013f1d2ee42b7505410e2e00df98_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{lll} 1(-1)+2(0)+3(2) & 1(1)+2(-1)+3(3) & 1(0)+2(1)+3(4) \\ 0(-1)+1(0)+0(2) & 0(1)+1(-1)+0(3) & 0(0)+1(1)+0(4) \\ 1(-1)+1(0)+0(2) & 1(1)+1(-1)+0(3) & 1(0)+1(1)+0(4) \end{array}\right]\\ =\left[\begin{array}{ccc} 5 & 8 & 14 \\ 0 & -1 & 1 \\ -1 & 0 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20c4a3322adc5550d12d6c51c31cd5ac_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-940891d7eeb234d5c1b9cbf4327d1db4_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{ccc} -1(1)+1(0)+0(1) & (-1) 2+1(1)+0(1) & (-1) 3+1(0)+0(0) \\ 0(1)+(-1) 0+1(1) & (0) 2+1(-1)+1(1) & (0) 3+0(-1)+1(0) \\ 2(1)+3(0)+4(1) & 2(2)+3(1)+4(1) & 2(3)+3(0)+4(0) \end{array}\right] \\ =\left[\begin{array}{ccc} -1 & -1 & -3 \\ 1 & 0 & 0 \\ 6 & 11 & 6 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-edd6af7bf96d10094a792cdefbba7284_l3.png)
![Rendered by QuickLaTeX.com \text { }\left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right] \neq\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a551f96aca879e1e19af23baf7d25e47_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &A^{2}-5 A+6 I=\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]-5\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]+6\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &=\left[\begin{array}{lll} 4+0+1 & 0+0-1 & 2+0+0 \\ 4+2+3 & 0+1-3 & 2+3+0 \\ 2-2+0 & 0-1-0 & 1-3+0 \end{array}\right]-\left[\begin{array}{ccc} 10 & 0 & 5 \\ 10 & 5 & 15 \\ 5 & -5 & 0 \end{array}\right]+\left[\begin{array}{lll} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{array}\right] \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-635f8626628550aad7c391a308bf5852_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{array}{l} =\left[\begin{array}{ccc} 5 & -1 & 2 \\ 9 & -2 & 5 \\ 0 & -1 & -2 \end{array}\right]-\left[\begin{array}{ccc} 10 & 0 & 5 \\ 10 & 5 & 15 \\ 5 & -5 & 0 \end{array}\right]+\left[\begin{array}{ccc} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{array}\right] \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-04dc370ab07157528701f3254c10f018_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{ccc} 5-10+6 & -1-0+0 & 2-5+0 \\ 9-10+0 & -2-5+6 & 5-15+0 \\ 0-5+0 & -1+5+0 & -2+0+6 \end{array}\right] \\ =\left[\begin{array}{ccc} 1 & -1 & -3 \\ -1 & -1 & -10 \\ -5 & 4 & 4 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c40482c486ab015274a3bc455b34e605_l3.png)
![Rendered by QuickLaTeX.com A=\begin{bmatrix}1&0&2\\0&2&1\\2&0&3\\\end{bmatrix} A^{2} \\=A * A=\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right] \\ =\left[\begin{array}{lll} 1+0+4 & 0+0+0 & 2+0+6 \\ 0+0+2 & 0+4+0 & 0+2+3 \\ 2+0+6 & 0+0+0 & 4+0+9 \end{array}\right] \\ =\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b694c409dd14718e28b15bbdd973a476_l3.png)
![Rendered by QuickLaTeX.com 6 A^{2} =6\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]=\left[\begin{array}{ccc} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{array}\right] \\ A^{3} =A^{2} \times A \\ =\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right] \\ =\left[\begin{array}{lll} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb8226fd84f309168ea8c20eec8738b2_l3.png)
![Rendered by QuickLaTeX.com A^{3} - 6 A^{2}+7 A+2 I=\left[\begin{array}{ccc} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{array}\right]-\left[\begin{array}{ccc} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{array}\right]+\left[\begin{array}{ccc} 7 & 0 & 14 \\ 0 & 14 & 7 \\ 14 & 0 & 21 \end{array}\right]+\left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array}\right]\\ =\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c17b534af2d4af9ddd59e3b3e66761e_l3.png)
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr} 3 & -2 \\ 4 & -2 \end{array}\right] \text { and } I=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\\ A^{2}=k A-2 I \Rightarrow\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]=k\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]-2\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\\ \Rightarrow\left[\begin{array}{cc} 9-8 & -6+4 \\ 12-8 & -8+4 \end{array}\right]=\left[\begin{array}{cc} 3 k & -2 k \\ 4 k & -2 k \end{array}\right]-\left[\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ll} 1 & -2 \\ 4 & -4 \end{array}\right]=\left[\begin{array}{ll} 3 k-2 & -2 k-0 \\ 4 k-0 & -2 k-2 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdbfc5ee9888bc2885e4fe8eb317b98a_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \text { L.H.S. } I+A=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]+\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]=\left[\begin{array}{cc} 1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1 \end{array}\right] \\ \text { Now, } I-A=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]-\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]=\left[\begin{array}{cc} 1 & \tan \frac{\alpha}{2} \\ -\tan \frac{\alpha}{2} & 1 \end{array}\right] \\ \text { R.H.S. }=(I-A)\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]=\left[\begin{array}{cc} 1 & \tan \frac{\alpha}{2} \\ -\tan \frac{\alpha}{2} & 1 \end{array}\right]\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-692503b6fcfa700919c4d1d5b7669c9c_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &=\left[\begin{array}{ccc} \cos \alpha+\sin \alpha \tan \frac{\alpha}{2} & -\sin \alpha+\cos \alpha \tan \frac{\alpha}{2} \\ -\cos \alpha \tan \frac{\alpha}{2}+\sin \alpha & \sin \alpha \tan \frac{\alpha}{2}+\cos \alpha \\ \end{array}\right]\\ &\text {} \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-913532a6e25d0f84186415a01e778cf1_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos \alpha \cos \frac{\alpha}{2}+\sin \alpha \sin \frac{\alpha}{2}{\cos \frac{\alpha}{2}} & \frac{\alpha \sin \alpha \cos \frac{\alpha}{2}+\cos \alpha \sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \ \\ \hline \frac{-\cos \alpha \sin \frac{\alpha}{2}+\sin \alpha \cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{\sin \alpha \sin \frac{\alpha}{2}+\cos \alpha \cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0078e771b174f50320e2262731bacbf_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &=\left[\begin{array}{cc} \frac{\cos \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} & \frac{-\sin \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} \\ \frac{\sin \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} & \frac{\cos \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} \end{array}\right]=\left[\begin{array}{ccc} \frac{\cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{-\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \\ \frac{\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{\cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \end{array}\right]=\left[\begin{array}{cc} 1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1 \end{array}\right]\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f95a8fcd4cde16269dbe05e0a402d2fb_l3.png)