Pregunta 1. Deja 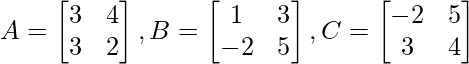
Encuentre cada uno de los siguientes:
(yo) A + B
(ii) A-B
(iii) 3A-C
(iv) AB
(v) BA
Solución:
(i)
(ii)
(iii)
(iv)
(v)
Pregunta 2. Calcula lo siguiente:
Solución:
(i)
(ii)
(iii)
(iv)
Pregunta 3. Calcula los productos indicados.
Solución:
(i)
(ii)
(iii)
(iv)
(v)
(vi)
Pregunta 4. Si  , entonces calcula (A + B) y (B – C). Además, verifique que A + (B – C) = (A + B) – C.
, entonces calcula (A + B) y (B – C). Además, verifique que A + (B – C) = (A + B) – C.
Solución:
Ahora tenemos que mostrar A + (B – C) = (A + B) – C
LHS = RHS
Por lo tanto, demostrado
Pregunta 5. Si 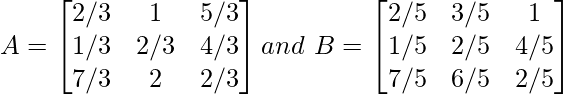 , entonces calcule 3A – 5B.
, entonces calcule 3A – 5B.
Solución:
Pregunta 6. Simplifica 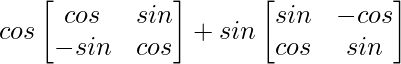
Solución:
= 1 = array identidad
Pregunta 7. Encuentra X e Y si
(i) 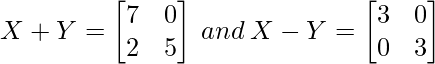
(ii) 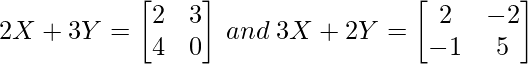
Solución:
(i) Dado:
Sumando (1) y (2), obtenemos
(ii) Dado:
Ahora, multiplicando la ecuación (1) por 2 y la ecuación (2) por 3 obtenemos
Restando la ecuación (4) de (3), obtenemos,
Pregunta 8. Encuentra X, si 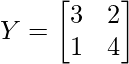 y
y 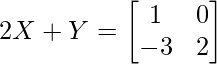
Solución:
Pregunta 9. Encuentra X e Y, si 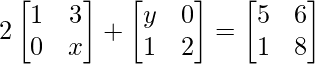
Solución:
Dado:
Igualando las entradas correspondientes, tenemos
2 + y = 5 y 2x + 2 = 8
y = 5 – 2 y 2(x + 1) = 8
y = 3 y x + 1 = 4
Por lo tanto, y = 3 y x = 3
Pregunta 10. Resuelva la ecuación para x, y, z y t, si 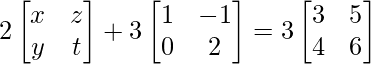
Solución:
Dado:
Al comparar ambos lados, tenemos
2x + 3 = 9 ⇒ 2x = 9 – 3 ⇒ 2x = 6 ⇒ x = 3
2z – 3 = 15 ⇒ 2z = 15 + 3 ⇒ 2z = 18 ⇒ z = 9
2y = 12 ⇒ y = 6
2t + 6 = 18 ⇒ 2t = 18 – 6 ⇒ 2t = 12 ⇒ t = 6
Por lo tanto, x = 3, y = 6, z = 9, t = 6
Capítulo 3 Arrays – Ejercicio 3.2 | conjunto 2
Publicación traducida automáticamente
Artículo escrito por kavyagupta0098 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com A+B=\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]+\left[\begin{array}{cc} 1 & 3 \\ -2 & 5 \end{array}\right] \\ =\left[\begin{array}{ll} 2+1 & 4+3 \\ 3-2 & 2+5 \end{array}\right] \\ =\left[\begin{array}{ll} 3 & 7 \\ 1 & 7 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e393f4a87f4b904215d929c9593b921_l3.png)
![Rendered by QuickLaTeX.com A-B=\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]-\left[\begin{array}{cc} 1 & 3 \\ -2 & 5 \end{array}\right] \\ =\left[\begin{array}{cc} 2-1 & 4-3 \\ 3 & -(-2) & 2-5 \end{array}\right] \\ =\left[\begin{array}{cc} 1 & 1 \\ 5 & -3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-478953432e19dbe17bb8427a4908d701_l3.png)
![Rendered by QuickLaTeX.com 3 A-C=3\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]-\left[\begin{array}{cc} -2 & 5 \\ 3 & 4 \end{array}\right] \\ =\left[\begin{array}{ll} 3 \times 2 & 3 \times 4 \\ 3 \times 3 & 3 \times 2 \end{array}\right]-\left[\begin{array}{cc} -2 & 5 \\ 3 & 4 \end{array}\right] \\ =\left[\begin{array}{lc} 6 & 12 \\ 9 & 6 \end{array}\right]-\left[\begin{array}{cc} -2 & 5 \\ 3 & 4 \end{array}\right] \\ =\left[\begin{array}{ll} 6+2 & 12-5 \\ 9 -3 & 6-4 \end{array}\right] \\ =\left[\begin{array}{ll} 8 & 7 \\ 6 & 2 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c66aa0dd6c6bd1c778f96428a0d2df48_l3.png)
![Rendered by QuickLaTeX.com A B=\left[\begin{array}{ll} 2 & 4 \\ 3 & 2 \end{array}\right]\left[\begin{array}{cc} 1 & 3 \\ -2 & 5 \end{array}\right]\\ =\left[\begin{array}{ll} 2(1)+4(-2) & 2(3)+4(5) \\ 3(1)+2(-2) & 3(3)+2(5) \end{array}\right]\\ =\left[\begin{array}{ll} 2-8 & 6+20 \\ 3-4 & 9+10 \end{array}\right]\\ =\left[\begin{array}{ll} -6 & 26 \\ -1 & 19 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc1d2c9cdcde55503987b6014870ae56_l3.png)
![Rendered by QuickLaTeX.com BA =\left[\begin{array}{cc} 1 & 3 \\ -2 & 5 \end{array}\right]\left[\begin{array}{cc} 2 & 4 \\ 3 & 2 \end{array}\right] \\ =\left[\begin{array}{cc} 1(2)+3(3) & 1(4)+3(2) \\ -2(2)+5(3) & -2(4)+5(2) \end{array}\right] \\ =\left[\begin{array}{rr} 2+9 & 4+6 \\ -4+15 & -8+10 \end{array}\right] \\ =\left[\begin{array}{cc} 11 & 10 \\ 11 & 2 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-50438532600587682c9d23822e341148_l3.png)
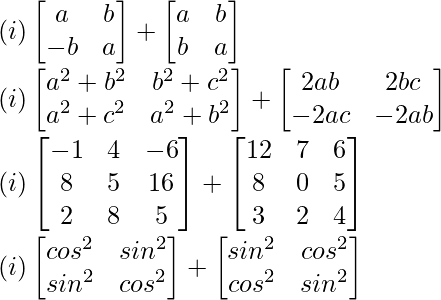
![Rendered by QuickLaTeX.com {\left[\begin{array}{cc} a & b \\ -b & a \end{array}\right]+\left[\begin{array}{cc} a & b \\ b & a \end{array}\right]} \\ =\left[\begin{array}{cc} a+a & b+b \\ -b+b & a+a \end{array}\right] \\ =\left[\begin{array}{cc} 2 a & 2 b \\ 0 & 2 a \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f89f20bdf4b80978129b6fd4c8ecf79e_l3.png)
![Rendered by QuickLaTeX.com {\left[\begin{array}{l} a^{2}+b^{2} & b^{2}+c^{2} \\ a^{2}+c^{2} & a^{2}+b^{2} \end{array}\right]+\left[\begin{array}{cc} 2 a b & 2 b c \\ -2 a c & -2 a b \end{array}\right]} \\ =\left[\begin{array}{ll} a^{2}+b^{2}+2 a b & b^{2}+c^{2}+2 b c \\ a^{2}+c^{2}-2 a c & a^{2}+b^{2}-2 a b \end{array}\right] \\ =\left[\begin{array}{c} (a+b)^{2}&(b+c)^{2} \\ (a-c)^{2} & (a-b)^{2} \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b4bf81268525c108da2e92e74d22fb22_l3.png)
![Rendered by QuickLaTeX.com {\left[\begin{array}{ccc} -1 & 4 & -6 \\ 8 & 5 & 16 \\ 2 & 8 & 5 \end{array}\right]+\left[\begin{array}{ccc} 12 & 7 & 6 \\ 8 & 0 & 5 \\ 3 & 2 & 4 \end{array}\right]} \\ =\left[\begin{array}{ccc} -1+12 & 4+7 & -6+6 \\ 8+8 & 5+0 & 16+5 \\ 2+3 & 8+2 & 5+4 \end{array}\right] \\ =\left[\begin{array}{ccc} 11 & 11 & 0 \\ 16 & 5 & 21 \\ 5 & 10 & 9 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e21bd1a4d82430ee9ae82fe38b6d769c_l3.png)
![Rendered by QuickLaTeX.com {\left[\begin{array}{ll} \cos ^{2} x & \sin ^{2} x \\ \sin ^{2} x & \cos ^{2} x \end{array}\right]+\left[\begin{array}{ll} \sin ^{2} x & \cos ^{2} x \\ \cos ^{2} x & \sin ^{2} x \end{array}\right]} \\ =\left[\begin{array}{cc} \cos ^{2} x+\sin ^{2} x & \cos ^{2} x+\sin ^{2} x \\ \sin ^{2} x+\cos ^{2} x & \cos ^{2} x+\sin ^{2} x \end{array}\right] \\ =\left[\begin{array}{ll} 1 & 1 \\ 1 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cdce3b7a1ed46f6ab4591fee33a4229a_l3.png)
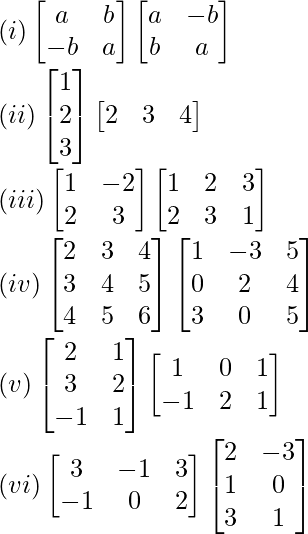
![Rendered by QuickLaTeX.com {\left[\begin{array}{cc} a & b \\ -b & a \end{array}\right]\left[\begin{array}{cc} a & -b \\ b & a \end{array}\right]} \\ =\left[\begin{array}{cc} a(a)+b(b) & a(-b)+b(a) \\ -b(a)+a(b) & -b(-b)+a(a) \end{array}\right] \\ =\left[\begin{array}{cc} a^{2}+b^{2} & -a b+a b \\ -a b+a b & b^{2}+a^{2} \end{array}\right] \\ =\left[\begin{array}{cc} a^{2}+b^{2} & 0 \\ 0 & b^{2}+a^{2} \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c4860d686e58b3dc0471d63ba32f2499_l3.png)
![Rendered by QuickLaTeX.com {\left[\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right]\left[\begin{array}{lll} 2 & 3 & 4 \end{array}\right]} \\ =\left[\begin{array}{lll} 1(2) & 1(3) & 1(4) \\ 2(2) & 2(3) & 2(4) \\ 3(2) & 3(3) & 3(4) \end{array}\right] \\ =\left[\begin{array}{lll} 2 & 3 & 4 \\ 4 & 6 & 8 \\ 6 & 9 & 12 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-44a7d98fb1d4a1e2b3a93a383f6a493a_l3.png)
![Rendered by QuickLaTeX.com {\left[\begin{array}{cc} 1 & -2 \\ 2 & 3 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 3 & 2 & 1 \end{array}\right]} \\ =\left[\begin{array}{llll} 1(1)-2(2) & 1(2)-2(3) & 1(3)-2(1) \\ 2(1)+3(2) & 2(2)+3(3) & 2(3)+3(1) \end{array}\right] \\ =\left[\begin{array}{lll} 1-4 & 2-6 & 3-2 \\ 2+6 & 4+9 & 6+3 \end{array}\right] \\ =\left[\begin{array}{ccc} -3 & -4 & 1 \\ 8 & 13 & 9 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a6a14b50b10c724786c59a5bffc32158_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} 2 & 3 & 4 \\ 3 & 4 & 5 \\ 4 & 5 & 6 \end{array}\right]\left[\begin{array}{rrr} 1 & -3 & 5 \\ 0 & 2 & 4 \\ 3 & 0 & 5 \end{array}\right] \\ =\left[\begin{array}{l} 2(1)+3(0)+4(3) & 2(-3)+3(2)+4(0) & 2(5)+3(4)+4(5) \\ 3(1)+4(0)+5(3) & 3(-3)+4(2)+5(0) & 3(5)+4(4)+5(5) \\ 4(1)+5(0)+6(3) & 4(-3)+5(2)+6(0) & 4(5)+5(4)+6(5) \end{array}\right] \\ =\left[\begin{array}{lll} 2+0+12 & -6+6+0 & 10+12+20 \\ 3+0+15 & -9+8+0 & 15+16+25 \\ 4+0+18 & -12+10+0 & 20+20+30 \end{array}\right] \\ =\left[\begin{array}{lll} 14 & 0 & 42 \\ 18 & -1 & 56 \\ 22 & -2 & 70 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2e8a2e9f36c80204b1abdcd3db1059ee_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 2 & 1 \\ 3 & 2 \\ -1 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 1 \\ -1 & 2 & 1 \end{array}\right] \\ =\left[\begin{array}{cccc} 2(1)+1(-1) & 2(0)+1(2) & 2(1)+1(1) \\ 3(1)+2(-1) & 3(0)+2(2) & 3(1)+2(1) \\ -1(1)+1(-1) & -1(0)+1(2) & -1(1)+1(1) \end{array}\right] \\ =\left[\begin{array}{ccc} 2-1 & 0+2 & 2+1 \\ 3-2 & 0+4 & 3+2 \\ -1-1 & 0+2 & -1+1 \end{array}\right] \\ =\left[\begin{array}{ccc} 1 & 2 & 3 \\ 1 & 4 & 5 \\ -2 & 2 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ffb07f29c4fed913156b9f85fd59f9e9_l3.png)
![Rendered by QuickLaTeX.com {\left[\begin{array}{ccc} 3 & -1 & 3 \\ -1 & 0 & 2 \end{array}\right]\left[\begin{array}{cc} 2 & -3 \\ 1 & 0 \\ 3 & 1 \end{array}\right]} \\ =\left[\begin{array}{cc} 3(2)-1(1)+3(3) & 3(-3)-1(0)+3(1) \\ -1(2)+0(1)+2(3) & -1(-3)+0(0)+2(1) \end{array}\right] \\ =\left[\begin{array}{cc} 6-1+9 & -9-0+3 \\ -2+0+6 & 3+0+2 \end{array}\right] \\ =\left[\begin{array}{cc} 14 & -6 \\ 4 & 5 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b455f100dcf5f3c78423e49de2bd5afb_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} A+B=\left[\begin{array}{ccc} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{array}\right]+\left[\begin{array}{ccc} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{array}\right] \\ {\left[\begin{array}{ccc} 1+3 & 2-1 & -3+2 \\ 5+4 & 0+2 & 2+5 \\ 1+2 & -1+0 & 1+3 \end{array}\right]=\left[\begin{array}{cccc} 4 & 1 & -1 \\ 9 & 2 & 7 \\ 3 & -1 & 4 \end{array}\right]} & \\ B-C=\left[\begin{array}{ccc} 3 & -1 & 2 \\ 4 & 2 & 5 \\ 2 & 0 & 3 \end{array}\right]-\left[\begin{array}{ccc} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{array}\right]=\left[\begin{array}{ccc} 3-4 & -1-1 & 2-2 \\ 4-0 & 2-3 & 5-2 \\ 2-1 & 0+2 & 3-3 \end{array}\right]=\left[\begin{array}{ccc} -1 & -2 & 0 \\ 4 & -1 & 3 \\ 1 & 2 & 0 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-701d668d0f44f488d498cdfe86391860_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow\left[\begin{array}{ccc} 1 & 2 & -3 \\ 5 & 0 & 2 \\ 1 & -1 & 1 \end{array}\right]+\left[\begin{array}{ccc} -1 & -2 & 0 \\ 4 & -1 & 3 \\ 1 & 2 & 0 \end{array}\right]=\left[\begin{array}{ccc} 4 & 1 & -1 \\ 9 & 2 & 7 \\ 3 & -1 & 4 \end{array}\right]-\left[\begin{array}{ccc} 4 & 1 & 2 \\ 0 & 3 & 2 \\ 1 & -2 & 3 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ccc} 1-1 & 2-2 & -3+0 \\ 5+4 & 0-1 & 2+3 \\ 1+1 & -1+2 & 1+0 \end{array}\right]=\left[\begin{array}{ccc} 4-4 & 1-1 & -1-2 \\ 9-0 & 2-3 & 7-2 \\ 3-1 & -1+2 & 4-3 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ccc} 0 & 0 & -3 \\ 9 & -1 & 5 \\ 2 & 1 & 1 \end{array}\right]=\left[\begin{array}{ccc} 0 & 0 & -3 \\ 9 & -1 & 5 \\ 2 & 1 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6a35d81c84808b2087014e88edbbc967_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} 3 A -5 B =3\left[\begin{array}{ccc} \frac{2}{3} & 1 & \frac{5}{3} \\ \frac{1}{3} & \frac{2}{3} & \frac{4}{3} \\ \frac{7}{3} & 2 & \frac{2}{3} \end{array}\right]-5\left[\begin{array}{ccc} \frac{2}{5} & \frac{3}{5} & 1 \\ \frac{1}{5} & \frac{2}{5} & \frac{4}{5} \\ \frac{7}{5} & \frac{6}{5} & \frac{2}{5} \end{array}\right] \\ =\left[\begin{array}{rrr} 2 & 3 & 5 \\ 1 & 2 & 4 \\ 7 & 6 & 2 \end{array}\right]-\left[\begin{array}{ccc}\\ 2 -2 & 3-3 & 5 -5 \\ 1 -1 & 2-2 & 4 -4 \\ 7 -7 & 6-6 & 2 -2 \end{array}\right]=\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d3f599a80c024c274e52e0e3e99f858_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &\cos \theta\left[\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]+\sin \theta\left[\begin{array}{cc} \sin \theta & -\cos \theta \\ \cos \theta & \sin \theta \end{array}\right]\\ &=\left[\begin{array}{cc} \cos ^{2} \theta & \sin \theta \cos \theta \\ -\sin \theta \cos \theta & \cos ^{2} \theta \end{array}\right]+\left[\begin{array}{cc} \sin ^{2} \theta & \sin \theta \cos \theta \\ \sin \theta \cos \theta & \sin ^{2} \theta \end{array}\right]\\ &=\left[\begin{array}{cc} \cos ^{2} \theta+\sin ^{2} \theta & \sin \theta \cos \theta-\sin \theta \cos \theta \\ -\sin \theta \cos \theta+\sin \theta \cos \theta & \cos ^{2} \theta+\sin ^{2} \theta \end{array}\right]\\ &=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] \quad\left[\because \sin ^{2} \theta+\cos ^{2} \theta=1 \mid\right.\\ \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3c7f99fb10b3fd7952321e07b40e425f_l3.png)
![Rendered by QuickLaTeX.com X+Y=\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right] \ \ \ -(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-63a42ec1f14f522958065e2725b5fd85_l3.png)
![Rendered by QuickLaTeX.com X-Y=\left[\begin{array}{ll} 3 & 0 \\ 0 & 3 \end{array}\right] \ \ \ -(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3e0889478ba977ba0cd274917bd5f4b9_l3.png)
![Rendered by QuickLaTeX.com 2 X=\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right]+\left[\begin{array}{ll} 3 & 0 \\ 0 & 3 \end{array}\right]\\ =\left[\begin{array}{ll} 7+3 & 0+0 \\ 2+0 & 5+3 \end{array}\right]\\ =\left[\begin{array}{cc} 10 & 0 \\ 2 & 8 \end{array}\right]\\ \Rightarrow X=\frac{1}{2}\left[\begin{array}{ll} 10 & 0 \\ 2 & 8 \end{array}\right]=\left[\begin{array}{ll} 5 & 0 \\ 1 & 4 \end{array}\right]\\ X+Y=\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ll} 5 & 0 \\ 1 & 4 \end{array}\right]+Y=\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right]\\ \Rightarrow Y=\left[\begin{array}{ll} 7 & 0 \\ 2 & 5 \end{array}\right]-\left[\begin{array}{ll} 5 & 0 \\ 1 & 4 \end{array}\right]\\ \Rightarrow Y=\left[\begin{array}{ll} 2 & 0 \\ 1 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-005a90b06bb8a2efe5a0cd3844eea99a_l3.png)
![Rendered by QuickLaTeX.com 2 X+3 Y=\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right] \ \ \ -(1)\\ 3 X+2 Y=\left[\begin{array}{cc} 2 & -2 \\ -1 & 5 \end{array}\right] \ \ \ -(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1907be18a0e5ccbd3d4c3444b79ca80_l3.png)
![Rendered by QuickLaTeX.com 4 X+6 Y=\left[\begin{array}{ll} 4 & 6 \\ 8 & 0 \end{array}\right] \ \ \ -(3)\\ 9 X+6 Y=\left[\begin{array}{cc} 6 & -6 \\ -3 & 15 \end{array}\right] \ \ \ -(4)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d535d27bd75c4a9e1e125d36072172e_l3.png)
![Rendered by QuickLaTeX.com (4 X+6 Y)-(9 X+6 Y)=\left[\begin{array}{ll} 4 & 6 \\ 8 & 0 \end{array}\right]-\left[\begin{array}{cc} 6 & -6 \\ -3 & 15 \end{array}\right]\\ \Rightarrow-5 X=\left[\begin{array}{cc} 4-6 & 6-(-6) \\ 8-(-3) & 0-15 \end{array}\right]\\ =\left[\begin{array}{cc} -2 & 12 \\ 11 & -15 \end{array}\right]\\ \Rightarrow X=-\frac{1}{5}\left[\begin{array}{cc} -2 & 12 \\ 11 & -15 \end{array}\right]=\left[\begin{array}{cc} \frac{2}{5} & \frac{-12}{5} \\ \frac{-11}{5} & 3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8e756535bce2012b5e83e91bd72e84e3_l3.png)
![Rendered by QuickLaTeX.com 2 X +3 Y =\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right] \\ \Rightarrow 2\left[\begin{array}{ll} \frac{2}{5} & \frac{-12}{5} \\ \frac{-11}{5} & 3 \end{array}\right]+3 Y =\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right] \\ \Rightarrow\left[\begin{array}{ll} \frac{4}{5} & \frac{-24}{5} \\ \frac{-22}{5} & 6 \end{array}\right]+3 Y =\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right] \\ \Rightarrow 3 Y =\left[\begin{array}{ll} 2 & 3 \\ 4 & 0 \end{array}\right]-\left[\begin{array}{cc} \frac{4}{5} & \frac{-24}{5} \\ \frac{-22}{5} & 6 \end{array}\right] \\ \Rightarrow Y=\frac{1}{3}\left[\begin{array}{cc} \frac{6}{5} & \frac{39}{5} \\ \frac{42}{5} & -6 \end{array}\right] \\ \Rightarrow Y=\left[\begin{array}{cc} \frac{2}{5} & \frac{13}{5} \\ \frac{14}{5} & -2 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb3eae74f4a0443242c6d9218195e415_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} 2 X+Y=\left[\begin{array}{cc} 1 & 0 \\ -3 & 2 \end{array}\right] \\ \Rightarrow 2 X+\left[\begin{array}{cc} 3 & 2 \\ 1 & 4 \end{array}\right]=\left[\begin{array}{cc} 1 & 0 \\ -3 & 2 \end{array}\right] \\ \Rightarrow 2 X=\left[\begin{array}{cc} 1 & 0 \\ -3 & 2 \end{array}\right]-\left[\begin{array}{cc} 3 & 2 \\ 1 & 4 \end{array}\right] \\ \Rightarrow 2 X=\left[\begin{array}{cc} 1-3 & 0-2 \\ -3 & -1 & 2-4 \end{array}\right] \\ \Rightarrow 2 X=\left[\begin{array}{cc} -2 & -2 \\ -4 & -2 \end{array}\right] \\ \Rightarrow X=\frac{1}{2}\left[\begin{array}{cc} -2 & -2 \\ -4 & -2 \end{array}\right] \\ ∴ X=\left[\begin{array}{cc} -1 & -1 \\ -2 & -1 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fdc3517e7dfcc2105dc3340a3ffd2903_l3.png)
![Rendered by QuickLaTeX.com 2\left[\begin{array}{ll} 1 & 3 \\ 0 & x \end{array}\right]+\left[\begin{array}{ll} y & 0 \\ 1 & 2 \end{array}\right]=\left[\begin{array}{ll} 5 & 6 \\ 1 & 8 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ll} 2 & 6 \\ 0 & 2 x \end{array}\right]+\left[\begin{array}{ll} y & 0 \\ 1 & 2 \end{array}\right]=\left[\begin{array}{ll} 5 & 6 \\ 1 & 8 \end{array}\right]\\ \Rightarrow\left[\begin{array}{cc} 2+y & 6 \\ 1 & 2 x+x \end{array}\right]^{2}=\left[\begin{array}{cc} 5 & 6 \\ 1 & 8 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1a79fc3437cda0a5754b41b84860308_l3.png)
![Rendered by QuickLaTeX.com 2\left[\begin{array}{ll} x & z \\ y & t \end{array}\right]+3\left[\begin{array}{cc} 1 & -1 \\ 0 & 2 \end{array}\right]=3\left[\begin{array}{ll} 3 & 5 \\ 4 & 6 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ll} 2 x & 2 z \\ 2 y & 2 t \end{array}\right]+\left[\begin{array}{cc} 3 & -3 \\ 0 & 6 \end{array}\right]=\left[\begin{array}{cc} 9 & 15 \\ 12 & 18 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ll} 2 x+3 & 2 z-3 \\ 2 y+0 & 2 t+6 \end{array}\right]=\left[\begin{array}{cc} 9 & 15 \\ 12 & 18 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-82b0cc69e7249a449d3e43b1140801fd_l3.png)