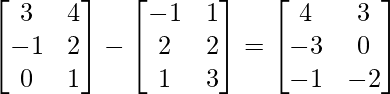
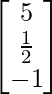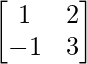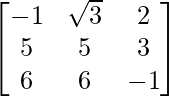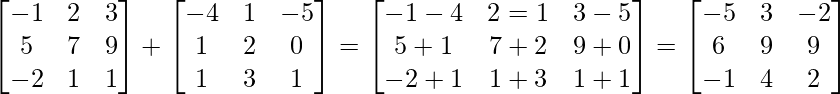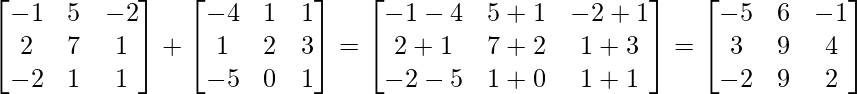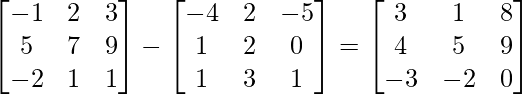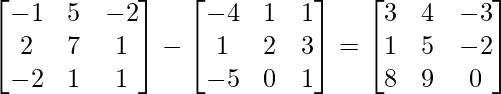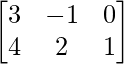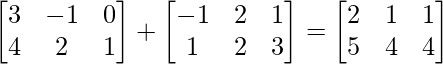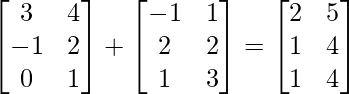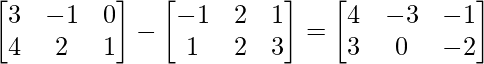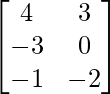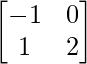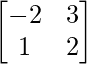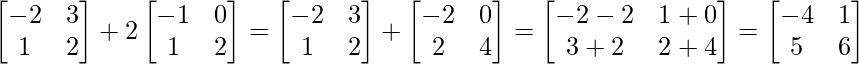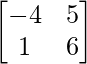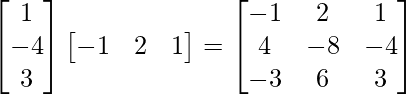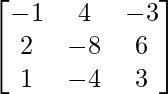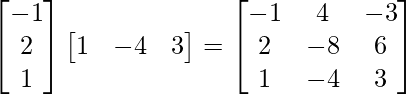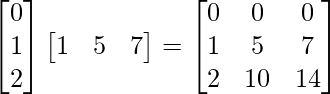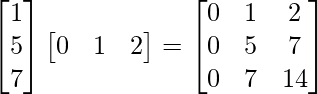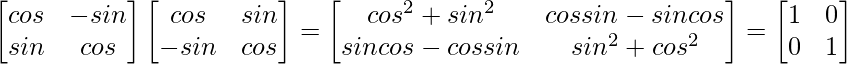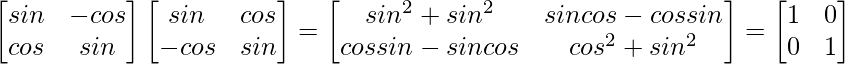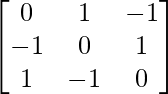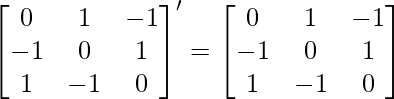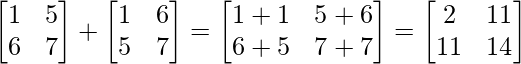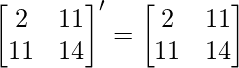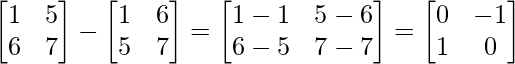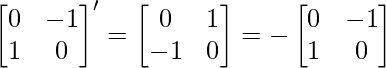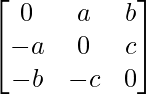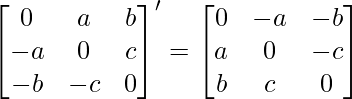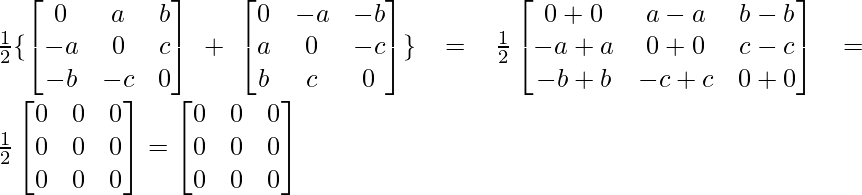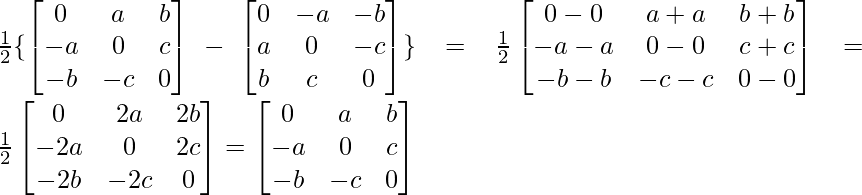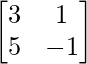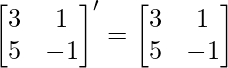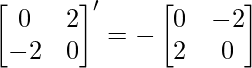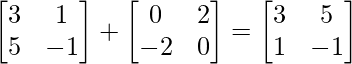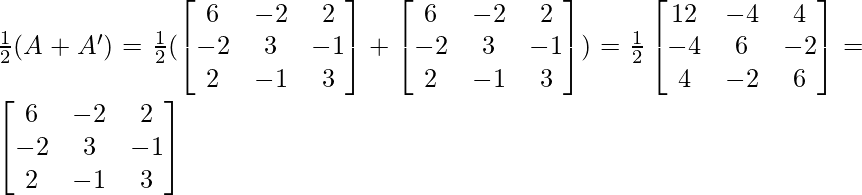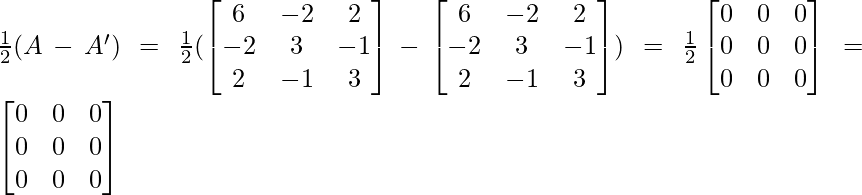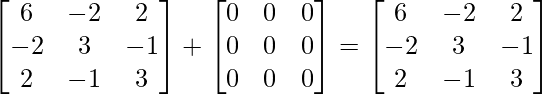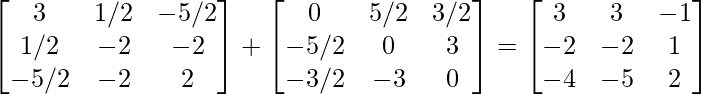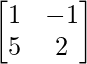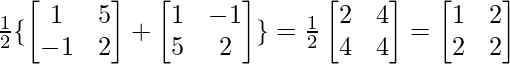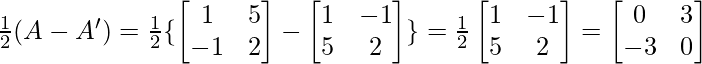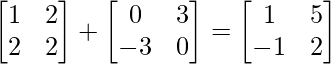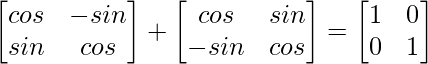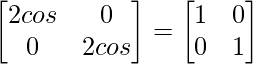Pregunta 1. Encuentra la transpuesta de cada una de las siguientes arrays:
(i) 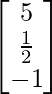
(ii) 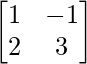
(iii) 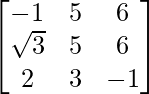
Solución:
(i) Sea A =
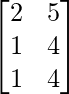
∴Transpuesta de A = A’ = A T =
(ii) Sea A =
∴Transpuesta de A = A’ = AT =
(iii) Sea A =
∴Transpuesta de A = A’ = AT =
Pregunta 2. Si A = 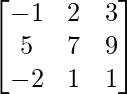 y B =
y B = 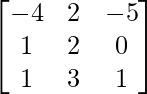 entonces verifica que:
entonces verifica que:
(i) (A+B)’ = A’+B’
(ii) (AB)’ = A’-B’
Solución:
(yo) A+B =
IZQ = (A+B)’ =
RHS = A’+B’ =
∴LHS = RHS
Por lo tanto, probado.
(ii) AB =
IZQ = (AB)’
RHS = A’-B’ =
∴ LHS = RHS
Por lo tanto, probado.
Pregunta 3. Si A’ = 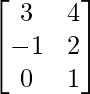 y B =
y B = 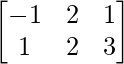 , entonces verifica que:
, entonces verifica que:
(yo) (A+B)’=A’+B’
(ii) (AB)’=A’-B’
Solución:
Dados A’=
y B=
entonces, (A’)’ = A =
(yo) A+B =
∴ IZQ = (A+B)’=
DCH= A’+B’ =
∴ LHS = RHS
Por lo tanto, probado.
(ii) AB =
∴ IZQ = (AB)’=
RHS= A’-B’ =
∴ LHS = RHS
Por lo tanto, probado.
Pregunta 4. Si A’ = 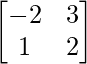 y B =
y B = 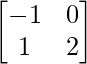 entonces encuentra (A+2B)’.
entonces encuentra (A+2B)’.
Solución:
Dado: A’ =
y B =
entonces (A’)’ =A=
Ahora, A+2B =
∴(A+2B)’ =
Pregunta 5. Para las arrays A y B, verifique que (AB)′ = B′A′, donde
(i) A = 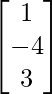 y B =
y B = ![]()
(ii) A = ![]() y B =
y B =![]()
Solución:
(i) AB = =
∴ IZQ = (AB)′ =
RHS= B′A’ =
∴ LHS = RHS
Por lo tanto, probado.
(ii) AB =
∴ IZQ = (AB)′ =
Ahora, RHS=B’A’ =
∴ LHS = RHS
Por lo tanto, probado.
Pregunta 6. Si (i) A = 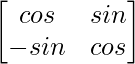 , entonces verifique que A′ A = I.
, entonces verifique que A′ A = I.
(ii) A = 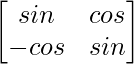 , luego verifique que A′ A = I.
, luego verifique que A′ A = I.
Solución:
(i)
= yo = lado derecho
∴ LHS = RHS
(ii)
= yo = lado derecho
∴ LHS = RHS
Pregunta 7. (i) Demuestre que la array A 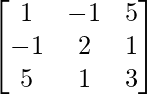 = es una array simétrica.
= es una array simétrica.
(ii) Demuestre que la array A 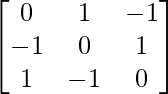 = es una array simétrica.
= es una array simétrica.
(i) Dado: A =
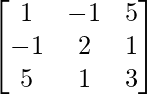
Ahora, A’=
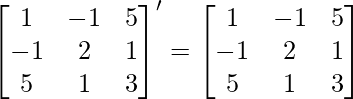
∵ A = A’
∴ A es una array simétrica.
(ii) Dado: A =
Ahora, A’=
∵ A = A’
∴ A es una array simétrica.
Pregunta 8. Para la array A =  , verifique que:
, verifique que:
(i) (A + A′) es una array simétrica
(ii) (A – A′) es una array simétrica oblicua
Solución:
(i) Dado: A =
Sea B = (A+A’) =
Ahora, B’ = (A+A’)’ =
∵ B = B’
∴ B=(A+A’) es una array simétrica.
(ii) Dado: A =
Sea B = (A-A’) =
Ahora, B’ = (A-A’)’ =
∵ -B = B’
∴ B=(A-A’) es una array simétrica oblicua.
Pregunta 9. Encuentra 1/2(A+A’) y 1/2(A-A’), cuando A = 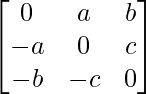 .
.
Solución:
Dado: A =
∴A’ =
Ahora, A+A’ = +
Ahora, A-A’ =
Pregunta 10. Exprese las siguientes arrays como la suma de una array simétrica y una simétrica oblicua:
(i) 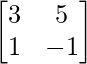
(ii) 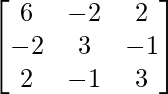
(iii) 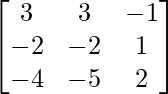
(iv) 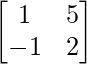
Solución:
(i) Dado: A =
⇒ A’=
Sea P =
y Q =
Ahora, P =
…..(1)
& P’ =
∵ P=P’
∴ P es una array simétrica.
Ahora, Q =
…..(2)
& Q’ =
∵ -Q=Q’
∴ Q es una array simétrica oblicua.
Sumando (1) y (2), obtenemos,
Por lo tanto, A = P + Q
(ii) Dado:
⇒ A’=
PAG =
…..(1)
Q =
……(2)
Sumando (1) y (2), obtenemos,
\begin{bmatrix}0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\end{bmatrix}
Por lo tanto, A = P + Q
(iii) Dado: A =
⇒ A’=
P = }
…..(1)
P =
……(2)
Sumando (1) y (2), obtenemos
}
Por lo tanto, A = P + Q
(iv) Dado: A =
⇒ A’=
PAG =
…..(1)
Q =
…..(2)
Sumando (1) y (2), obtenemos
Por lo tanto, A = P + Q
Pregunta 11. Si A, B son arrays simétricas del mismo orden, entonces AB – BA es una
(A) Array simétrica sesgada (B) Array simétrica
(C) Array cero (D) Array identidad
Solución:
Dado: A y B son arrays simétricas.
⇒ A=A’
⇒ B=B’
Ahora, (AB – BA)’ =(AB)’-(BA)’ [∵ (XY)’=X’-Y’]
=B’A’-A’B’ [∵ (XY)’=Y’X’]
=BA-AB [∵ Dado]
= -(AB-BA)
∴(AB-BA) es una array simétrica oblicua.
∴ La opción (A) es correcta.
Pregunta 12. Si A = 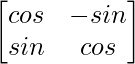 , y A + A′ = I, entonces el valor de α es
, y A + A′ = I, entonces el valor de α es
(A)π/6 (B) π/3
(C) π (D)3π/2
Solución:
Al comparar ambos lados, obtenemos
2cosα = 1
⇒ cosα =
⇒ cosα = cos
⇒ α =
∴ La opción (B) es correcta.
Publicación traducida automáticamente
Artículo escrito por kavyagupta0098 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA