Capítulo 3 Arrays – Ejercicio 3.4 | Serie 1
Pregunta 11. 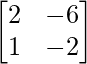
Solución:
}
Pregunta 12. 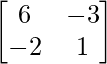
Solución:
Aquí, ambos elementos de R 2 de LHS son 0.
Por lo tanto, A -1 no existe.
Pregunta 13. 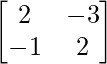
Solución:
Pregunta 14. 
Solución:
Aquí, ambos elementos de R2 de LHS son 0.
Por lo tanto, A-1 no existe.
Pregunta 15. 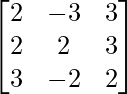
Solución:
Sea A=
WKT , A=IA
[Tex]\begin{array}{l} {\left[\mathrm{R}{1} \rightarrow \mathrm{R}{1}-\mathrm{R}_{3}\right]}\\\ \ {\left[\mathrm{R}{1} \rightarrow(-1) \mathrm{R}{1}\right]} \end{array}[/Tex]
Por lo tanto, A – 1 =
Pregunta 16. 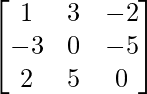
Solución:
Sea A=
WKT , A=IA
[Tex]\begin{alineado} &\left[\begin{array}{lll} 1 & 0 & 10 \\ 0 & 1 & -4 \\ 0 & 0 & 25 \end{array}\right]=\ izquierda[\begin{array}{ccc} -5 & 0 & 3 \\ 2 & 0 & -1 \\ -15 & 1 & 9 \end{array}\right] \text { A }\left[R_{ 1} \rightarrow R_{1}-3 R_{2}\right. \text { y } R_{3} \rightarrow R_{3}-9 R_{2}\\ &\left[\begin{array}{ccc} 1 & 0 & 10 \\ 0 & 1 & -4 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} -5 & 0 & 3 \\ 2 & 0 & -1 \\ -3 / 5 & 1 / 25 & 9 / 25 \end{array}\right] \text { A }\left[R_{1} \rightarrow \frac{1}{25} R_{3}\right]\\ &\left[\begin{array {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} 1 & -\frac{2 {5} & -\frac{3}{5} \\ -\frac{2}{5} & \frac{4}{25} &
Pregunta 17. 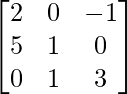
Solución:
Sea A=
WKT , A=IA
Pregunta 18. Las arrays A y B serán inversas entre sí solo si:
(A) AB = BA
(B) AB = BA = 0
(C) AB = 0, BA = yo
(D) AB = BA = yo
Solución:
Según la definición de inversa de array cuadrada,
La opción (D) es correcta
es decir AB=BA=I
Publicación traducida automáticamente
Artículo escrito por kavyagupta0098 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com \begin{aligned} &\text { Let } A=\left[\begin{array}{cc} 2 & -6 \\ 1 & -2 \end{array}\right]\\ &\text { W.K.T. , } A=IA \Rightarrow\left[\begin{array}{cc} 2 & -6 \\ 1 & -2 \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] \text { A }\\ &\Rightarrow\left[\begin{array}{ll} 1 & -2 \\ 2 & -6 \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right] A\left[R_{1} \leftrightarrow R_{2}\right]\\ &\Rightarrow\left[\begin{array}{rr} 1 & -2 \\ 0 & -2 \end{array}\right]=\left[\begin{array}{rr} 0 & 1 \\ 1 & -2 \end{array}\right] \text { A }\left[R_{2} \rightarrow R_{2}-2 R_{1}\right] \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f085b04f9c9448cfd7448d7370de6a8a_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \Rightarrow\left[\begin{array}{cc} 1 & -2 \\ 0 & 1 \end{array}\right]=\left[\begin{array}{ll} 0 & 1 \\ -1 / 2 & 1 \end{array}\right] \mathrm{A}\left[\mathrm{R}{2} \rightarrow \frac{-1}{2} \mathrm{R}{2}\right] \\ \Rightarrow\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]=\left[\begin{array}{ll} -1 & 3 \\ -1 / 2 & 1 \end{array}\right] \mathrm{A}\left[\mathrm{R}{1} \rightarrow \mathrm{R}{1}+2 \mathrm{R}_{2}\right] \\ \mathrm{Therefore, A}^{-1}=\left[\begin{array}{ll} -1 & 3 \\ -1 / 2 & 1 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-745ed912355ddaf131a4d14dbb868e1c_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \text { Let } A=\left[\begin{array}{cc} 6 & -3 \\ -2 & 1 \end{array}\right] \\ \text { W.K.T. , } A=IA \Rightarrow\left[\begin{array}{cc} 6 & -3 \\ -2 & 1 \end{array}\right]=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] \mathrm{A} \\ \Rightarrow\left[\begin{array}{cc} 1 & -1 / 2 \\ -2 & 1 \end{array}\right]=\left[\begin{array}{cc} 1 / 6 & 0 \\ 0 & 1 \end{array}\right] \text { A }\left[R_{1} \rightarrow \frac{1}{6} R_{1}\right] \\ \Rightarrow\left[\begin{array}{cc} 1 & -1 / 2 \\ 0 & 0 \end{array}\right]=\left[\begin{array}{cc} 1 / 6 & 0 \\ 1 / 3 & 1 \end{array}\right] \text { A }\left[R_{2} \rightarrow R_{2}+2 R_{1}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43263a12f1c71c331c41a7bcbd693cb9_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \text { Let } A=\left[\begin{array}{cc} 2 & -3 \\ -1 & 2 \end{array}\right] \\ \text { W.K.T. , } A=IA \Rightarrow\left[\begin{array}{cc} 2 & -3 \\ -1 & 2 \end{array}\right]=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] \text { A } \\ \Rightarrow\left[\begin{array}{cc} 1 & -1 \\ -1 & 2 \end{array}\right]=\left[\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array}\right] \text { A }\left[R_{1} \rightarrow R_{1}+R_{2}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ab635c4635ea43b2cc872a0158c0516f_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \Rightarrow\left[\begin{array}{ll} 1 & -1 \\ 0 & 1 \end{array}\right]=\left[\begin{array}{ll} 1 & 1 \\ 1 & 2 \end{array}\right] \text { A }\left[R_{2} \rightarrow R_{2}+R_{1}\right] \\ \Rightarrow\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]=\left[\begin{array}{ll} 2 & 3 \\ 1 & 2 \end{array}\right] \text { A }\left[R_{1} \rightarrow R_{1}+R_{2}\right] \\ Therefore, A^{-1}=\left[\begin{array}{ll} 2 & 3 \\ 1 & 2 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c6effefe0431d49bced5ae5d4057cbda_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &\text { Let } A=\left[\begin{array}{ll} 2 & 1 \\ 4 & 2 \end{array}\right]\\ &\text { W.K.T. ,} A=IA \Rightarrow\left[\begin{array}{ll} 2 & 1 \\ 4 & 2 \end{array}\right]=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] \text { A }\\ \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e10dd037fb312be3e471739cf7489af2_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \Rightarrow\left[\begin{array}{cc} 1 & 1 / 2 \\ 4 & 2 \end{array}\right]=\left[\begin{array}{cc} 1 / 2 & 0 \\ 0 & 1 \end{array}\right] \text { A }\left[R_{1} \rightarrow \frac{1}{2} R_{1}\right] \\ \Rightarrow\left[\begin{array}{ll} 1 & 1 / 2 \\ 0 & 0 \end{array}\right]=\left[\begin{array}{ll} 1 / 2 & 0 \\ -2 & 1 \end{array}\right] \text { A }\left[R_{2} \rightarrow R_{2}-4 R_{1}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5be4fa9b5d5e43382948cad21b80cdc2_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} \Rightarrow\left[\begin{array}{ccc} 1 & 1 & -1 \\ 0 & 0 & 5 \\ 0 & -5 & 5 \end{array}\right]=\left[\begin{array}{rrr} -1 & 0 & 1 \\ 2 & 1 & -2 \\ 3 & 0 & -2 \end{array}\right] \mathrm{A}\left[\mathrm{R}{2} \rightarrow \mathrm{R}{2}-2 \mathrm{R}{1} \text { and } \mathrm{R}{3} \rightarrow \mathrm{R}{3}-3 \mathrm{R}{1}\right] \\ \left.=\left[\begin{array}{ccc} 1 & 1 & -1 \\ 0 & -5 & 5 \\ 0 & 0 & 5 \end{array}\right]=\begin{array}{rrr} -1 & 0 & 1 \\ 3 & 0 & -2 \\ 2 & 1 & -2 \end{array}\right] \mathrm{A}\left[\mathrm{R}{2} \leftrightarrow \mathrm{R}{3}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-91f67b2420edbfdfae4b8ada502ee5d4_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} {\left[\begin{array}{ccc} 1 & 1 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 5 \end{array}\right]=\left[\begin{array}{ccc} -1 & 0 & 1 \\ -3 / 5 & 0 & 2 / 5 \\ 2 & 1 & -2 \end{array}\right] \mathrm{A} \quad\left[\mathrm{R}{2} \rightarrow\left(\frac{-1}{5}\right) \mathrm{R}{2}\right]} \\ \left.\left[\begin{array}{rrr} 1 & 0 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 5 \end{array}\right]=\begin{array}{rrr} -2 / 5 & 0 & 3 / 5 \\ 2 & 0 & 2 / 5 \\ 2 & 1 & -2 \end{array}\right] \mathrm{A}\left[\mathrm{R}{1} \rightarrow \mathrm{R}{1}-\mathrm{R}_{2}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b6e8066e18bd4d075b11f91f7d6d2841_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} {\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} -2 / 5 & 0 & 3 / 5 \\ -3 / 5 & 0 & 2 / 5 \\ 2 / 5 & 1 / 5 & -2 / 5 \end{array}\right] \mathrm{A}\left[\mathrm{R}{3} \rightarrow \frac{1}{5} \mathrm{R}{3}\right]} \\ {\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} -2 / 5 & 0 & 3 / 5 \\ -1 / 5 & 1 / 5 & 0 \\ 2 / 5 & 1 / 5 & -2 / 5 \end{array}\right] \mathrm{A}\left[R_{2} \rightarrow R_{2}+R_{3}\right]} \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-581bfa9be11cdb6df7e74ace30d43010_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} -2 / 5 & 0 & 3 / 5 \\ -1 / 5 & 1 / 5 & 0 \\ 2 / 5 & 1 / 5 & -2 / 5 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54b0164036fca5396e3ad3e54c1f3a76_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &\left[\begin{array}{ccc} 2 & 0 & -1 \\ 5 & 1 & 0 \\ 0 & 1 & 3 \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &\left[\begin{array}{ccc} 2 & 0 & -1 \\ 1 & 1 & 2 \\ 0 & 1 & 3 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ -2 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] \text { A }\left[R_{2} \rightarrow R_{2}-2 R_{1}\right]\\ &\left[\begin{array}{ccc} 1 & 1 & 2 \\ 2 & 0 & -1 \\ 0 & 1 & 3 \end{array}\right]=\left[\begin{array}{rrr} -2 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{array}\right] \text { A }\left[R_{1} \leftrightarrow R_{2}\right]\\ &\left[\begin{array}{ccc} 1 & 1 & 2 \\ 0 & -2 & -5 \\ 0 & 1 & 3 \end{array}\right]=\left[\begin{array}{ccc} -2 & 1 & 0 \\ 5 & -2 & 0 \\ 0 & 0 & 1 \end{array}\right] A\left[R_{2} \rightarrow R_{2}-2 R_{1}\right]\\ &\left[\begin{array}{ccc} 1 & 1 & 2 \\ 0 & 1 & 3 \\ 0 & -2 & -5 \end{array}\right]=\left[\begin{array}{ccc} -2 & 1 & 0 \\ 0 & 0 & 1 \\ 5 & -2 & 0 \end{array}\right] A \quad R_{2} \leftrightarrow R_{3} \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eda89883bbc02503618bea4de055e782_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} {\left[\begin{array}{ccc} 1 & 0 & -1 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} -2 & 1 & -1 \\ 0 & 0 & 1 \\ 5 & -2 & 2 \end{array}\right] \text { A }\left[\mathrm{R}{1} \rightarrow \mathrm{R}{1}-\mathrm{R}{2} \text { and } \mathrm{R}{3} \rightarrow \mathrm{R}{3}+2 \mathrm{R}{2}\right]} \\ {\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{array}\right] \text { A }\left[\mathrm{R}{1} \rightarrow \mathrm{R}{1}+\mathrm{R}{3} \text { and } \mathrm{R}{2} \rightarrow \mathrm{R}{2}-3 \mathrm{R}{3}\right]} \\ \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5b8f97e869904e191f1ef71ce493227d_l3.png)
![Rendered by QuickLaTeX.com Therefore,A^{-1}=\left[\begin{array}{ccc} 3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-303f45d4ec9e5ffb4143936bde9bcc59_l3.png)