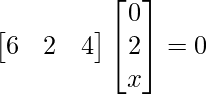
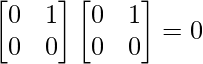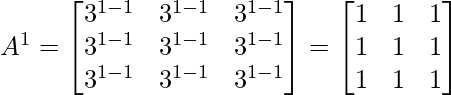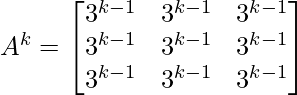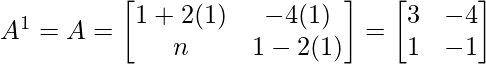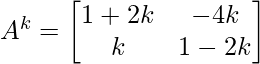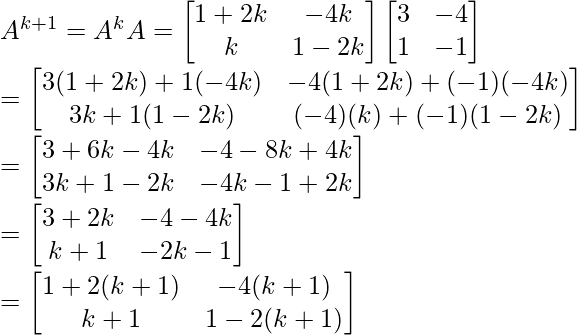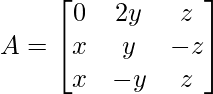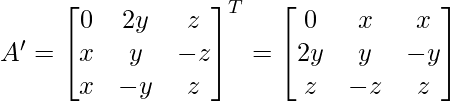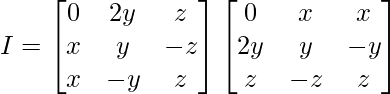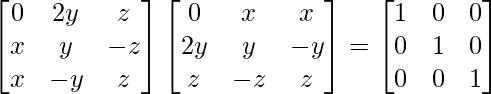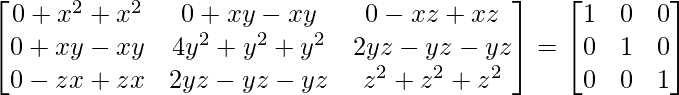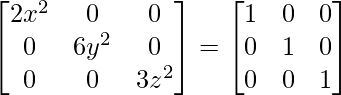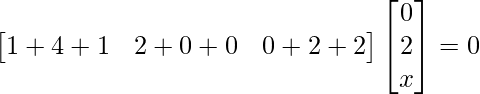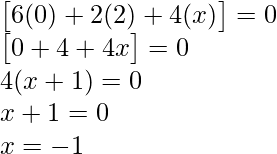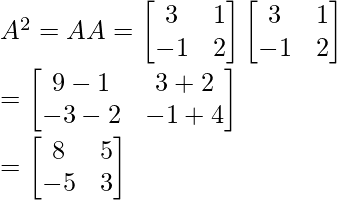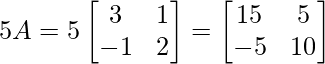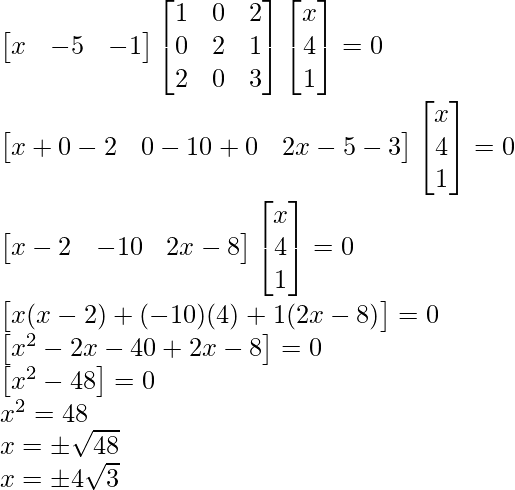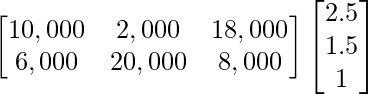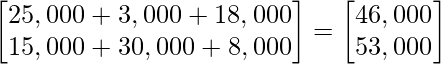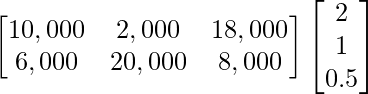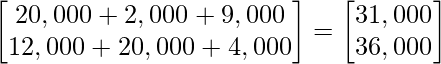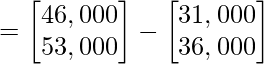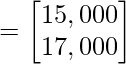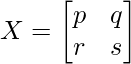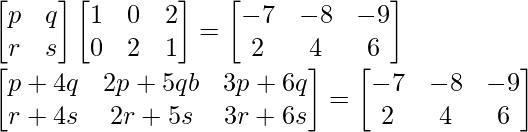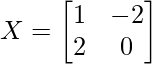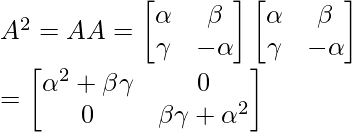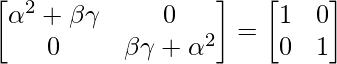Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 3 Arrays – Ejercicio misceláneo en el Capítulo 3

Posted on by Rudeus Greyrat

Pregunta 1: Sea 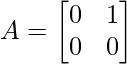 A =\begin{barray} 0 y 1\\ 0 y 0 \end{barray} , muestre que (aI + bA) n = a n I + na n – 1 bA, donde I es la array identidad de orden 2 y n ∈ N .

Solución:

Usando inducción matemática,

Paso 1: Verifiquemos si n=1

(aI + bA) n = (aI + bA) 1 = (aI + bA)

a n yo + na n – 1 bA = aI + 1a 1 – 1 bA = (aI + bA)

Es cierto para P(1)

Paso 2: Ahora toma n=k

(aI + bA) k = a k I + ka k – 1 bA …………………(1)

Paso 3: Verifiquemos si es cierto para n = k+1

(aI + bA) k+1 = (aI + bA) k (aI + bA)

= (a k I + ka k – 1 bA) (aI + bA)

= a k+1 I×I + ka k bAI + a k bAI + ka k-1 b 2 AA

AA = \begin{bmatrix} 0 y 1\\ 0 y 0 \end{bmatrix}\begin{bmatrix} 0 y 1\\ 0 y 0 \end{bmatrix} = 0

= a k+1 I×I + ka k bAI + a k bAI + 0

= a k+1 I + (k+1)a k+1-1 bA

= P(k+1)

Por lo tanto, P(n) es verdadera.

Pregunta 2: Si 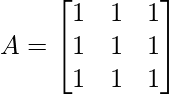 A =\begin{barray} 1 & 1 &1\\ 1 & 1 &1\\ 1 & 1 &1 \end{barray} , prueba que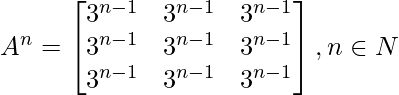 A^n =\begin{barray} 3^{n-1} & 3^{n-1} &3^{n-1}\\ 3^{n-1} & 3^{n-1} & 3 ^{n-1}\\ 3^{n-1} & 3^{n-1} & 3^{n-1} \end{barray} ,n\in N

Solución:

Usando inducción matemática,

Paso 1 : Verifiquemos si n=1

A^1 =\begin{bmatrix} 3^{1-1} & 3^{1-1} &3^{1-1}\\ 3^{1-1} & 3^{1-1} & 3^{1-1}\\ 3^{1-1} & 3^{1-1} & 3^{1-1} \end{bmatrix}=\begin{bmatrix} 1 & 1 &1\\ 1 & 1 &1\\ 1 & 1 &1 \end{bmatrix}

Es cierto para P(1)

Paso 2 : Ahora toma n=k

A^k =\begin{bmatrix} 3^{k-1} & 3^{k-1} &3^{k-1}\\ 3^{k-1} & 3^{k-1} &3^{k-1}\\ 3^{k-1} & 3^{k-1} &3^{k-1} \end{bmatrix}

Paso 3: Verifiquemos si es cierto para n = k+1

A^{k+1}=A^kA=\begin{bmatrix} 3^{k-1} & 3^{k-1} &3^{k-1}\\ 3^{k-1} & 3^{k-1} &3^{k-1}\\ 3^{k-1} & 3^{k-1} &3^{k-1} \end{bmatrix} \begin{bmatrix} 1 & 1 &1\\ 1 & 1 &1\\ 1 & 1 &1 \end{bmatrix}\\ A^{k+1} = \begin{bmatrix} 3^k & 3^k &3^k\\ 3^k & 3^k &3^k\\ 3^k & 3^k &3^k \end{bmatrix}\\ A^{k+1} = \begin{bmatrix} 3^{k+1-1} & 3^{k+1-1} &3^{k+1-1}\\ 3^{k+1-1} & 3^{k+1-1} &3^{k+1-1}\\ 3^{k+1-1} & 3^{k+1-1} &3^{k+1-1} \end{bmatrix}

= P(k+1)

Por lo tanto, P(n) es verdadera.

Pregunta 3: Si 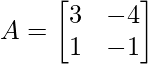 A =\begin{bmatrix} 3 & -4\\ 1 & -1 \end{bmatrix}, demuestre que  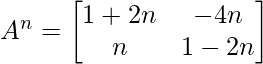A^n =\begin{bmatrix} 1+2n & -4n\\ n & 1-2n \end{bmatrix}  ,donde n es cualquier número entero positivo.

Solución:

Usando inducción matemática,

Paso 1: Verifiquemos si n=1

A^1 = A =\begin{bmatrix} 1+2(1) & -4(1)\\ n & 1-2(1) \end{bmatrix}=\begin{bmatrix} 3 & -4\\ 1 & -1 \end{bmatrix}

Es cierto para P(1)

Paso 2: Ahora toma n=k

A^k =\begin{bmatrix} 1+2k & -4k\\ k & 1-2k \end{bmatrix}

Paso 3: Verifiquemos si es cierto para n = k+1

A^{k+1} = A^kA =\begin{bmatrix} 1+2k & -4k\\ k & 1-2k \end{bmatrix}\begin{bmatrix} 3 & -4\\ 1 & -1 \end{bmatrix}\\ = \begin{bmatrix} 3(1+2k)+1(-4k) & -4(1+2k)+(-1)(-4k)\\ 3k+1(1-2k) & (-4)(k)+(-1)(1-2k) \end{bmatrix}\\ = \begin{bmatrix} 3+6k-4k & -4-8k+4k\\ 3k+1-2k & -4k-1+2k \end{bmatrix}\\ = \begin{bmatrix} 3+2k & -4-4k\\ k+1 & -2k-1 \end{bmatrix}\\ = \begin{bmatrix} 1+2(k+1) & -4(k+1)\\ k+1 & 1-2(k+1) \end{bmatrix}\\

= P(k+1)

Por lo tanto, P(n) es verdadera.

Pregunta 4. Si A y B son arrays simétricas, demuestre que AB – BA es una array asimétrica.

Solución:

Como se menciona que A y B son arrays simétricas,

A’ = A y B’ = B

(AB – BA)’ = (AB)’ – (BA)’   (usando, (AB)’ = A’ – B’)

= B’A’ – A’B’                      (usando, (AB)’ = B’A’)

= BA – AB

(AB – BA)’ = – (AB – BA)

Por lo tanto, AB – BA es una array simétrica oblicua

Pregunta 5. Muestre que la array B′AB es simétrica o sesgadamente simétrica según que A sea simétrica o sesgadamente simétrica.

Solución:

Tomemos A como array simétrica

A’ = A

Después,

(B’AB)’ = {B'(AB)}’

= (AB)’ (B’)’ (usando, (AB)’ = B’A’)

= B’A’ (B) (usando, (AB)’ = B’A’ y (B’)’ = B)

= B’A B

Como, aquí (B′AB)’ = B’A B. Es una array simétrica.

Tomemos A como array sesgada

A’ = -A

Después,

(B’AB)’ = {B'(AB)}’

= (AB)’ (B’)’ (usando, (AB)’ = B’A’)

= B’A’ (B) (usando, (AB)’ = B’A’ y (B’)’ = B)

= B'(-A) B

= – B’A B

Como, aquí (B′AB)’ = -B’A B. Es una array sesgada.

Por lo tanto, podemos concluir que B′AB es simétrico o simétrico sesgado según que A sea simétrico o simétrico sesgado.

Pregunta 6. Encuentra los valores de x, y, z si la array 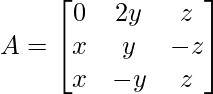 A =\begin{bmatrix} 0 & 2y &z\\ x & y &-z\\ x & -y &z \end{bmatrix}  satisface la ecuación A′A = I

Solución:

A =\begin{bmatrix} 0 & 2y &z\\ x & y &-z\\ x & -y &z \end{bmatrix}

A' =\begin{bmatrix} 0 & 2y &z\\ x & y &-z\\ x & -y &z \end{bmatrix}^T=\begin{bmatrix} 0 & x &x\\ 2y & y &-y\\ z & -z &z \end{bmatrix}

A’A = I =\begin{bmatrix} 0 & 2y &z\\ x & y &-z\\ x & -y &z \end{bmatrix}\begin{bmatrix} 0 & x &x\\ 2y & y &-y\\ z & -z &z \end{bmatrix}

\begin{bmatrix} 0 & 2y &z\\ x & y &-z\\ x & -y &z \end{bmatrix}\begin{bmatrix} 0 & x &x\\ 2y & y &-y\\ z & -z &z \end{bmatrix} = \begin{bmatrix} 1 & 0 &0\\ 0 & 1 &0\\ 0 & 0 &1 \end{bmatrix}

\begin{bmatrix} 0+x^2+x^2 & 0+xy-xy &0-xz+xz\\ 0+xy-xy & 4y^2+y^2+y^2 &2yz-yz-yz\\ 0-zx+zx & 2yz-yz-yz &z^2+z^2+z^2 \end{bmatrix} = \begin{bmatrix} 1 & 0 &0\\ 0 & 1 &0\\ 0 & 0 &1 \end{bmatrix}

\begin{bmatrix} 2x^2 & 0 &0\\ 0 & 6y^2 &0\\ 0 & 0 &3z^2 \end{bmatrix} = \begin{bmatrix} 1 & 0 &0\\ 0 & 1 &0\\ 0 & 0 &1 \end{bmatrix}

Evaluando los valores, tenemos

2×2 = 1

x = ± \frac{1}{\sqrt{2}}

6 años 2 = 1

y = ± \frac{1}{\sqrt{6}}

3z 2 = 1

z = ± \frac{1}{\sqrt{3}}

Pregunta 7: ¿Para qué valores de x : \begin{bmatrix} 1 & 2 &1 \end{bmatrix} \begin{bmatrix} 1 & 2 &0\\ 2 & 0 &1\\ 1 & 0 &2 \end{bmatrix} \begin{bmatrix} 0\\ 2\\ x \end{bmatrix} = 0

Solución:

\begin{bmatrix} 1 & 2 &1 \end{bmatrix} \begin{bmatrix} 1 & 2 &0\\ 2 & 0 &1\\ 1 & 0 &2 \end{bmatrix} \begin{bmatrix} 0\\ 2\\ x \end{bmatrix} = 0

\begin{bmatrix} 1+4+1 & 2+0+0 &0+2+2 \end{bmatrix} \begin{bmatrix} 0\\ 2\\ x \end{bmatrix} = 0

\begin{bmatrix} 6 & 2 &4 \end{bmatrix} \begin{bmatrix} 0\\ 2\\ x \end{bmatrix} = 0

\begin{bmatrix} 6(0) + 2(2) +4(x) \end{bmatrix}= 0\\ \begin{bmatrix} 0 + 4 +4x \end{bmatrix}= 0\\ 4(x+1) = 0\\ x+1 = 0\\ x = -1

Pregunta 8: Si 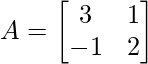 A =\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} , demuestre que A 2 – 5A + 7I = 0.

Solución:

A^2 = AA =\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}\\ = \begin{bmatrix} 9-1 & 3+2 \\ -3-2 & -1+4 \end{bmatrix}\\ = \begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix}

5A =5\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} =\begin{bmatrix} 15 & 5 \\ -5 & 10 \end{bmatrix}

7I =7\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}= \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix}

A 2 – 5A + 7I = \begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix}-\begin{bmatrix} 15 & 5 \\ -5 & 10 \end{bmatrix}+ \begin{bmatrix} 7 & 0 \\ 0 & 7 \end{bmatrix}\\ =\begin{bmatrix} 8-15+7 & 3-3+0 \\ -5+5+0 & 3-10+7 \end{bmatrix}\\ = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}

Por lo tanto demostrado!

Pregunta 9: Encuentra x, si 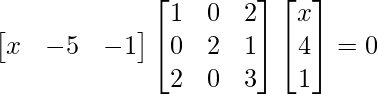\begin{bmatrix} x & -5 &-1 \end{bmatrix} \begin{bmatrix} 1 & 0 &2\\ 0 & 2 &1\\ 2 & 0 &3 \end{bmatrix} \begin{bmatrix} x\\ 4\\ 1 \end{bmatrix} = 0

Solución:

\begin{bmatrix} x & -5 &-1 \end{bmatrix} \begin{bmatrix} 1 & 0 &2\\ 0 & 2 &1\\ 2 & 0 &3 \end{bmatrix} \begin{bmatrix} x\\ 4\\ 1 \end{bmatrix} = 0\\ \begin{bmatrix} x+0-2 & 0-10+0 &2x-5-3 \end{bmatrix} \begin{bmatrix} x\\ 4\\ 1 \end{bmatrix} = 0\\ \begin{bmatrix} x-2 & -10 &2x-8 \end{bmatrix} \begin{bmatrix} x\\ 4\\ 1 \end{bmatrix} = 0\\ \begin{bmatrix} x(x-2) + (-10)(4) +1(2x-8) \end{bmatrix}= 0\\ \begin{bmatrix} x^2-2x -40+2x-8 \end{bmatrix}= 0\\ \begin{bmatrix} x^2-48 \end{bmatrix}= 0\\ x^2 = 48\\ x = \pm \sqrt{48}\\ x = \pm 4\sqrt{3}

Pregunta 10: Un fabricante produce tres productos x, y, z que vende en dos mercados.

Las ventas anuales se indican a continuación:

Mercado productos
yo 10,000 2,000 18,000
II 6,000 20,000 8,000

(a) Si los precios de venta unitarios de x, y y z son ₹ 2,50, ₹ 1,50 y ₹ 1,00, respectivamente, encuentre el ingreso total en cada mercado con la ayuda del álgebra matricial.

Solución:

Los ingresos totales en el mercado I y II se pueden organizar a partir de los datos dados de la siguiente manera:

\begin{bmatrix} 10,000 & 2,000 &18,000\\6,000 & 20,000 &8,000 \end{bmatrix} \begin{bmatrix} 2.5 \\ 1.5 \\1 \end{bmatrix}

Después de la multiplicación, obtenemos

\begin{bmatrix} 25,000 + 3,000 +18,000\\15,000 + 30,000 +8,000 \end{bmatrix}=\begin{bmatrix} 46,000\\53,000 \end{bmatrix}

Por lo tanto, los ingresos totales en el Mercado I y el Mercado II son ₹ 46 000 y ₹ 53 000, respectivamente.

(b) Si los costos unitarios de los tres productos anteriores son ₹ 2,00, ₹ 1,00 y 50 paise respectivamente. Encuentre la ganancia bruta.

Solución:

Los precios de costo totales de todos los productos en el mercado I y el mercado II se pueden organizar a partir de los datos dados de la siguiente manera:

\begin{bmatrix} 10,000 & 2,000 &18,000\\6,000 & 20,000 &8,000 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \\0.5 \end{bmatrix}

Después de la multiplicación, obtenemos

\begin{bmatrix} 20,000 + 2,000 +9,000\\12,000 + 20,000 +4,000 \end{bmatrix}=\begin{bmatrix} 31,000\\36,000 \end{bmatrix}

Como, Ganancia ganada = Ingreso total – Precio de costo

Beneficio obtenido =\begin{bmatrix} 46,000\\53,000 \end{bmatrix}-\begin{bmatrix} 31,000\\36,000 \end{bmatrix}

Beneficio obtenido = =\begin{bmatrix} 15,000\\17,000 \end{bmatrix}

Por lo tanto, las ganancias obtenidas en el Mercado I y el Mercado II son ₹ 15 000 y ₹ 17 000, respectivamente. Que es igual a ₹ 32,000

Pregunta 11. Encuentra la array X tal que 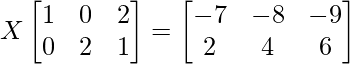X\begin{bmatrix} 1 & 0 &2\\ 0 & 2 &1 \end{bmatrix}= \begin{bmatrix} -7 & -8 &-9\\ 2 & 4 &6 \end{bmatrix}

Solución:

X\begin{bmatrix} 1 & 0 &2\\ 0 & 2 &1 \end{bmatrix}= \begin{bmatrix} -7 & -8 &-9\\ 2 & 4 &6 \end{bmatrix}

Aquí, RHS es una array de 2×3 y LHS es 2×3. Entonces, X será una array de 2 × 2.

Tomemos X como,

X= \begin{bmatrix} p & q \\ r & s \end{bmatrix}

Ahora resolviendo la array, tenemos

\begin{bmatrix} p & q\\ r & s \end{bmatrix}\begin{bmatrix} 1 & 0 &2\\ 0 & 2 &1 \end{bmatrix}= \begin{bmatrix} -7 & -8 &-9\\ 2 & 4 &6 \end{bmatrix}\\ \begin{bmatrix} p+4q & 2p+5qb &3p+6q\\ r+4s & 2r+5s &3r+6s \end{bmatrix}= \begin{bmatrix} -7 & -8 &-9\\ 2 & 4 &6 \end{bmatrix}\\

Igualando cada uno de ellos, obtenemos

p+4q = -7 ………..(1)

2p+5q = -8 ………….(2)

3p + 6q = -9

r + 4s = 2 …………(3)

2r + 5s = 4 ……………(5)

3r + 6s = 6

Resolviendo (1) y (2), obtenemos

p = 1 y q = -2

Resolviendo (3) y (4), obtenemos

r = 2 y s = 0

Por lo tanto, la array X es 

X= \begin{bmatrix} 1 & -2 \\ 2 & 0 \end{bmatrix}

Pregunta 12: Si A y B son arrays cuadradas del mismo orden tales que AB = BA, entonces demuestre por inducción que AB n = B n A. Además, demuestre que (AB) n = A n B n para todo n ∈ N .

Solución:

Usando inducción matemática,

Paso 1: Verifiquemos si n=1

AB n = AB 1 = AB

segundo norte UN = segundo 1 UN = BA

Es cierto para P(1)

Paso 2: Ahora toma n=k

AB k = segundo k A

Paso 3 : Verifiquemos si es cierto para n = k+1

AB (k+1) = AB k B

= B k AB

= B k+1 A

= P(k+1)

Por lo tanto, P(n) es verdadera.

Ahora, para (AB) n = A n B n

Usando inducción matemática,

Paso 1 : Verifiquemos si n=1

(AB) 1 = AB

segundo 1 un 1 = BA

Es cierto para P(1)

Paso 2 : Ahora toma n=k

(AB) k = UN k segundo k

Paso 3 : Verifiquemos si es cierto para n = k+1

(AB) (k+1) = (AB) k (AB)

= UN k B k AB

= A k+1 B k+1

= (AB) k+1

= P(k+1)

Por lo tanto, P(n) es verdadera.

Elige la respuesta correcta en las siguientes preguntas: 

Pregunta 13: Si 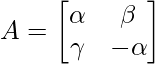 A= \begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix}  es tal que A² = I, entonces

(A) 1 + α² + βγ = 0 

(B) 1 – α² + βγ = 0

(C) 1 – α² – βγ = 0 

(D) 1 + α² – βγ = 0

Solución:

A^2 = AA= \begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix}\begin{bmatrix} \alpha & \beta \\ \gamma & -\alpha \end{bmatrix}\\ = \begin{bmatrix} \alpha^2+\beta\gamma & 0 \\ 0 & \beta\gamma+\alpha^2 \end{bmatrix}

Como, A 2 = I

\begin{bmatrix} \alpha^2+\beta\gamma & 0 \\ 0 & \beta\gamma+\alpha^2 \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}

α² + βγ = 1

1 – α² – βγ = 0

Por lo tanto, la opción (C) es correcta.

Pregunta 14. Si la array A es simétrica y asimétrica, entonces

(A) A es una array diagonal 

(B) A es una array cero

(C) A es una array cuadrada 

(D) Ninguno de estos

Solución:

Si la array A es simétrica y asimétrica, entonces

A = A’

y A = -A

Solo la array cero satisface ambas condiciones.

Por lo tanto, la opción (B) es correcta.

Pregunta 15. Si A es una array cuadrada tal que A 2 = A, entonces (I + A)³ – 7 A es igual a

(A) Un 

(B) Yo – A 

(C) yo 

(D) 3A

Solución:

(I + A)³ – 7 A = I 3 + A 3 + 3A^2 + 3AI^2 – 7A

= I3 + A3 + 3A 2 + 3A – 7A

= Yo + A 3 + 3A 2 – 4A

Como, A 2 = A

A3 = A 2 A = AA = A

Entonces, yo + A3 + 3A2 – 4A = yo + A + 3A – 4A = yo

Por lo tanto, la opción (C) es correcta.

Publicación traducida automáticamente

Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *