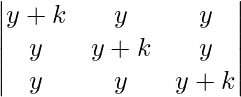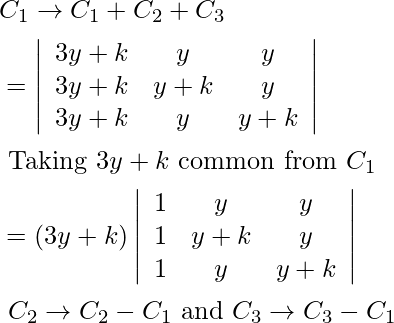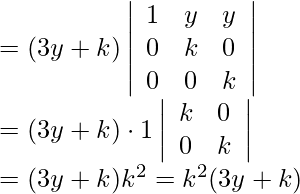Usando las propiedades de los determinantes y sin desarrollar en el Ejercicio 1 al 7, demuestre que:
Pregunta 1. 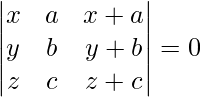
Solución:
IZQ=
C 1 → C 1 + C 2
=
Según las propiedades del determinante
=0 [∵ C 1 y C 3 son idénticos]
Ahora, LHS = RHS
Por lo tanto probado
Pregunta 2. 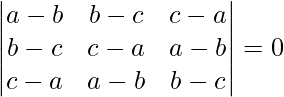
Solución:
IZQ=
=0 [∵ Todos los elementos de C 1 son 0]
Ahora, LHS = RHS
Por lo tanto probado
Pregunta 3. 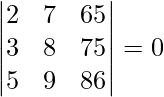
Solución:
IZQ=
C 3 →C 3 -C 1
=
=
=9 ×0=0 [∵C 2 y C 3 son idénticos]
Ahora, LHS = RHS
Por lo tanto probado
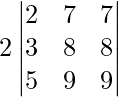
Pregunta 4. 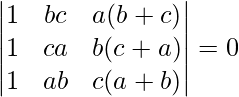
Solución:
IZQ=
=
Ahora, LHS = RHS
Por lo tanto probado
Pregunta 5. 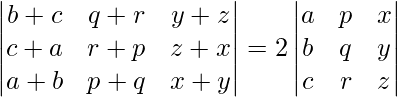
Solución:
IZQ=
Ahora, LHS = RHS
Por lo tanto probado
Pregunta 6. 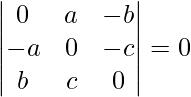
Solución:
Sea Δ=
Tomando (-1) común de cada fila
Δ=(-1) 3
Intercambiar filas y columnas
Δ=-
Ahora, Δ=-Δ
Δ+Δ=0
2Δ=0
Δ=0
Ahora, LHS = RHS
Por lo tanto probado
Pregunta 7. 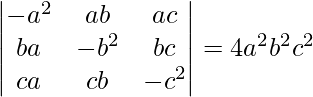
Solución:
IZQ=
Tomando a común de la Fila 1,
b de la fila 2,
c de la fila 3, tenemos
Ahora, LHS = RHS
Por lo tanto probado
Usando las propiedades de los determinantes, en los ejercicios 8 a 14, demuestre que:
Pregunta 8(i). 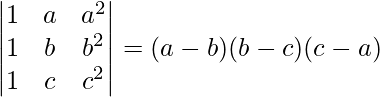
(ii)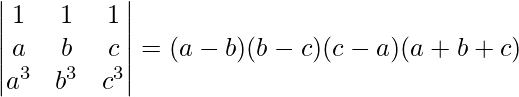
Solución:
(i) IZQ=
Ahora, LHS = RHS
Por lo tanto probado
(ii) LHS=
Ahora, LHS = RHS
Por lo tanto probado
Pregunta 9. 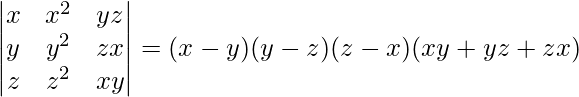
Solución:
IZQ=
Ahora, LHS = RHS
Por lo tanto probado
Pregunta 10.(i)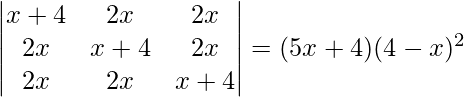
(ii)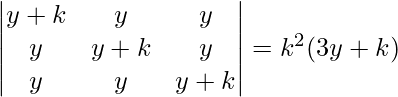
Solución:
(i) IZQ=
Ahora, LHS = RHS
Por lo tanto probado
(ii) LHS=
Ahora, LHS = RHS
Por lo tanto probado
Capítulo 4 Determinantes – Ejercicio 4.2 | conjunto 2
Publicación traducida automáticamente
Artículo escrito por kavyagupta0098 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
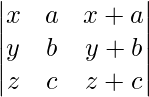
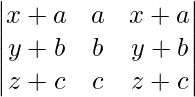
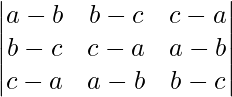
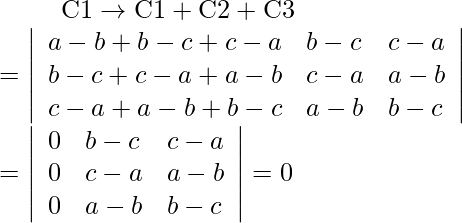


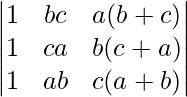
![Procesado por QuickLaTeX.com \text { } \mathrm{C}{3} \rightarrow \mathrm{C}{3}+\mathrm{C}_{2}\\\\ \text {= }\begin{vmatrix}1 & bc & ab+ac\\1 & ca & bc+ba\\1 & ab & ca+cb\end{vmatrix}\\\\ \text {= }\begin{vmatrix}1 & bc & ab+ac+bc\\1 & ca & bc+ba+ca\\1 & ab & ca+cb+ab\end{vmatrix}\\\\ \text {= }(ab+ac+bc)\begin{vmatrix}1 & bc & 1\\1 & ca &1\\1 & ab & 1\end{vmatrix}\\\\ \text {= }(ab+ac+bc)0\\\\ \text {= 0 }\qquad\qquad[∵Two \:columns\: are\: identical]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d07e2156440843e49226538afd2a83a_l3.png)
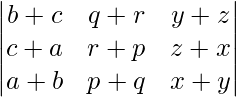
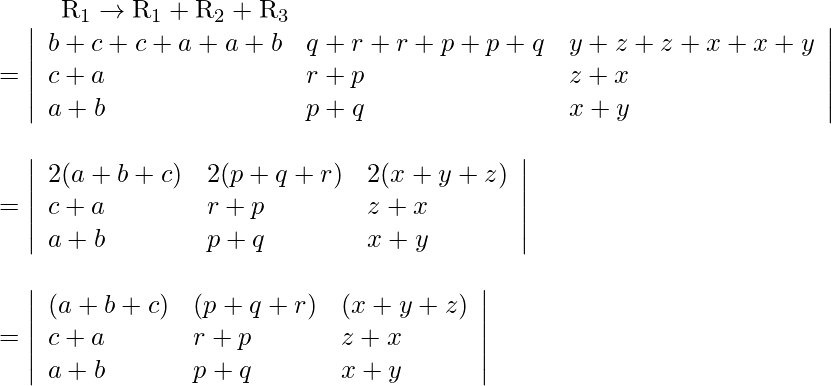
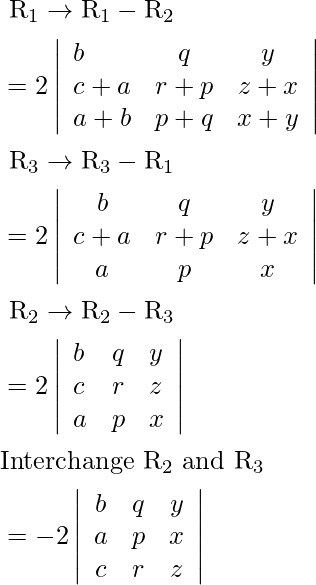
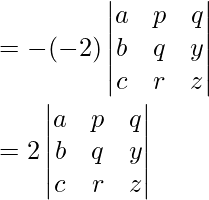
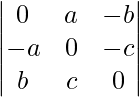
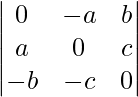
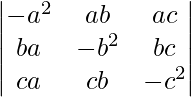
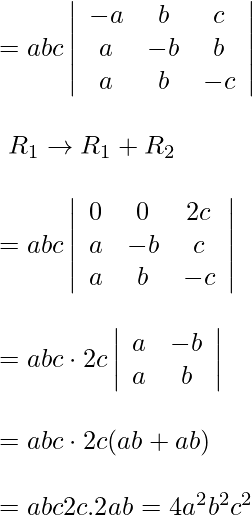
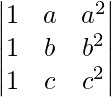
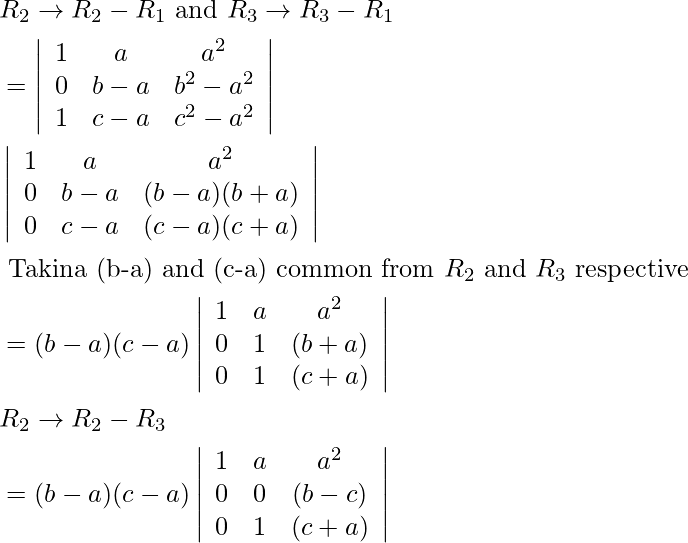
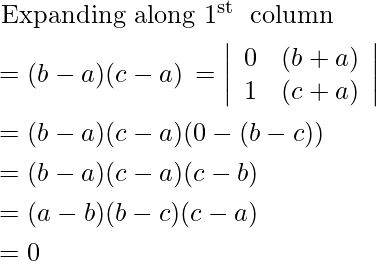
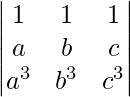
![Rendered by QuickLaTeX.com \begin{aligned} &\text { operating } C _{2} \rightarrow C _{2}- C _{1} \text { and } C _{3} \rightarrow C _{3}- C _{3}\\ &=\left|\begin{array}{ccc} 1 & 0 & 0 \\ a & b-a & c-a \\ a^{3} & b^{3}-a^{3} & c^{3}-a^{3} \end{array}\right|\\ &=1\left|\begin{array}{cc} b-a & c-a \\ b^{3}-a^{3} & c^{3}-a^{3} \end{array}\right|\\ &=1\left|\begin{array}{cc} b-a & c-a \\ (b-a)\left(b^{2}+a^{2}+a b\right) & (c-a)\left(c^{2}+a^{2}+a c\right) \end{array}\right|\\ &=(b-a)(c-a) \mid\left(b^{2}+a^{2}+a b\right) \quad\left(c^{2}+a^{2}+a c\right)\\ &=(b-a)(c-a)\left(c^{2}+a^{2}+a c-b^{2}-a^{2}-a b\right)\\ &=(b-a)(c-a)\left(c^{2}-b^{2}+a c-a b\right)\\ &=(b-a)(c-a)[(c-b)(c+b)+a(c-b)]\\ &=(b-a)(c-a)(c-b)(c+b+a)\\ &=-(a-b)(c-a)[-(b-c)(c+b+a)]\\ &=(a-b)(b-c)(c-a)(a+b+c) \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e421ec23971a0fd1bd4145d187b05255_l3.png)
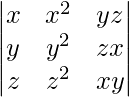
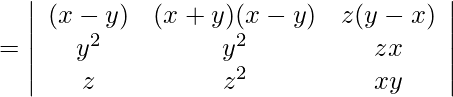
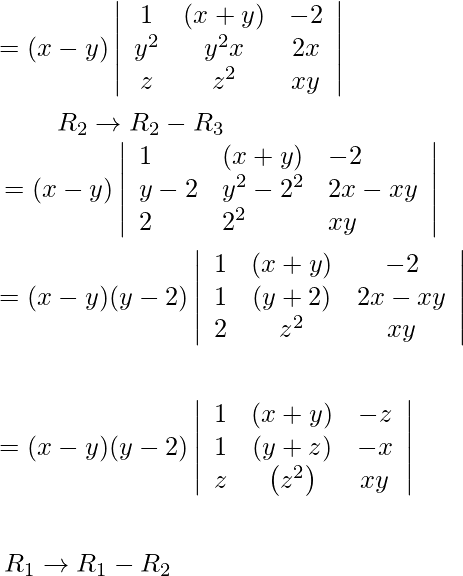
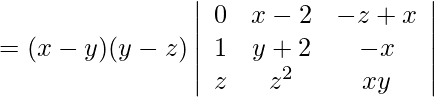
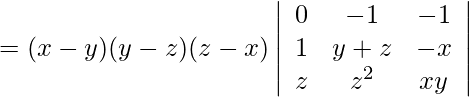
![Rendered by QuickLaTeX.com =(x-y)(y-z)(z-x)\left|\begin{array}{ccc} 0 & 0 & -1 \\ 1 & x+y+z & -x \\ z & z^{2}-xy & x y \end{array}\right|\\\\ =(x-y)(y-z)(z-x)[-1(z^{2}-xy-zx-zy-z^{2}]\\\\ =(x-y)(y-z)(z-x)(xy+zx+zy)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa845cebdd7e1dab6bd028ca9d46e340_l3.png)
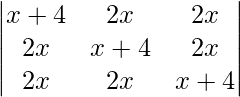
![Rendered by QuickLaTeX.com \begin{aligned} &R_{1} \rightarrow R_{1}+R_{2}+R_{3}\\ &=\left|\begin{array}{ccc} 5 x+4 & 5 x+4 & 5 x+4 \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4 \end{array}\right|\\ &\text { Taking } (5 x+4) \text { common from } R_{1}\\ &=(5 x+4)\left|\begin{array}{ccc} 1 & 1 & 1 \\ 2 x & x+4 & 2 x \\ 2 x & 2 x & x+4 \end{array} \right|.\\ &\text {} C _{2} \rightarrow C _{2}- C _{1} \text { and } \left. C _{3} \rightarrow C _{3}- C _{1}\right]\\ &=(5 x+4)\left|\begin{array}{ccc} 1 & 0 & 0 \\ 2 x & 4-x & 0 \\ 2 x & 0 & 4-x \end{array}\right|\\ &=(5 x+4) \cdot 1\left|\begin{array}{cc} 4-x & 0 \\ 0 & 4-x \end{array}\right|\\ &=(5 x+4)(4- x^{2}) \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11248103b61ad0dbd6910e2cb575112b_l3.png)