Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 4 Determinantes – Ejercicio 4.3

Pregunta 1. Encuentra el área del triángulo con vértices en el punto dado en cada uno de los siguientes:

(i) (1, 0), (6, 0), (4, 3)

(ii) (2, 7), (1, 1), (10, 8)

(iii) (–2, –3), (3, 2), (–1, –8)

Solución:

(i) (1, 0), (6, 0), (4, 3)

$Area\ of\ triangle=\frac{1}{2}\begin{vmatrix}1 & 0 & 1\\6&0&1\\4&3&1\end{vmatrix}\\=\frac{1}{2}[1(0-3)-0(6-4)+1(18-0)]\\=\frac{15}{2}square\ units$

(ii) (2, 7), (1, 1), (10, 8)

$Area\ of\ triangle=\frac{1}{2}\begin{vmatrix}2 & 7 & 1\\1&1&1\\10&8&1\end{vmatrix}\\=\frac{1}{2}[2(1-8)-7(1-10)+1(8-10)]\\=\frac{47}{2}square\ units$

(iii) (–2, –3), (3, 2), (–1, –8)

$Area\ of\ triangle=\frac{1}{2}\begin{vmatrix}-2 & -3 & 1\\3&2&1\\-1&-8&1\end{vmatrix}\\=\frac{1}{2}[-2(10)+3(4)-22]\\=15\ square\ units$

Pregunta 2. Demuestre que los puntos A (a, b + c), B (b, c + a), C (c, a + b) son colineales.

Solución:

Si el área del triángulo es igual a cero, entonces los puntos son colineales.

Por ejemplo: – Área del triángulo = 0

$Area\ of\ triangle=\frac{1}{2}\begin{vmatrix}a&b+c&1\\b&c+a&1\\c&a+b&1\end{vmatrix}\\ =\frac{1}{2}[a(c+a-a-b)-(b+c)(b-c)+1\{b(a+b)-c(c+a)\}]\\=\frac{1}{2}(ac-ab-b^2+c^2+ab+b^2-c^2-ac)\\0\\Hence,\ the\ points\ are\ collinear\ as\ the\ area\ of\ triangle\ is\ equal\ to\ zero$

Pregunta 3. Encuentra los valores de k si el área del triángulo es de 4 unidades cuadradas y los vértices son

(i) (k, 0), (4, 0), (0, 2)
(ii)(-2, 0), (0, 4), (0, k)

Solución:

(yo) (k, 0), (4, 0), (0, 2)

Dado: Área del triángulo = ±4 unidades cuadradas

es decir $\frac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}=4\\\frac{1}{2}[k(0-2)-0+1(8-0)]=4\\\frac{1}{2}(-2k+4)=4\\-k+4=4\\Here, -k+4=\pm4\\if,\\-k+4=4\ and-k+4=-4\\k=0\ and\ k=8$

(ii) (-2, 0), (0, 4), (0, k)

$\frac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}=4\\\frac{1}{2}\begin{vmatrix}-2&0&1\\0&4&1\\0&k&1\end{vmatrix}\\\frac{1}{2}(-8+2k)=4\\-k+4=4\\Here, -k+4=\pm4\\if,\\-k+4=4\ and-k+4=-4\\k=0\ and\ k=8$

Pregunta 4. (i) Encuentra la ecuación de la línea que une (1, 2) y (3, 6) usando determinantes.
(ii) Encuentre la ecuación de la línea que une (3, 1) y (9, 3) usando determinantes.

Solución:

(i) Encuentre la ecuación de la línea que une (1, 2) y (3, 6) usando determinantes.

Supongamos,

A(x, y) sea cualquier vértice de un triángulo

Todos los puntos están en una línea (colineales) si el área del triángulo es cero.

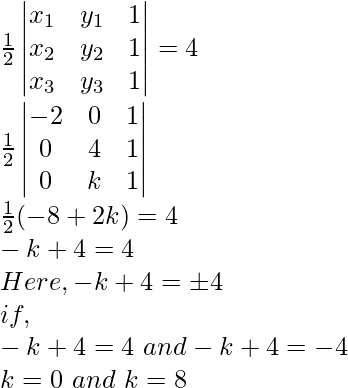
$\frac{1}{2}\begin{vmatrix}1&2&1\\3&6&1\\x&y&1\end{vmatrix}=0\\\frac{1}{2}[x(2-6)-y(1-3)+1(6-6)]=0\\-4x+2y=0\\y=2x\\Which\ is\ equation\ of\ a\ line.$

(ii) Encuentre la ecuación de la línea que une (3, 1) y (9, 3) usando determinantes.

Supongamos,

A(x, y) sea cualquier vértice de un triángulo

Todos los puntos están en una línea (colineales) si el área del triángulo es cero.

$\frac{1}{2}\begin{vmatrix}x&y&1\\3&1&1\\9&3&1\end{vmatrix}\\\frac{1}{2}[x(1-3)-y(3-9)+1(9-9)]=0\\-2x+6y=0\\x-3y=0\\It\ is\ a\ equation\ of\ line.$

Pregunta 5. Si el área del triángulo es de 35 unidades cuadradas con vértices (2, – 6), (5, 4) y (k, 4). Entonces k es
(A) 12 (B) –2 (C) –12, –2 (D) 12, –2

Solución:

(D) es la opción correcta.

Como:

$\frac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}=35\\\frac{1}{2}[2(4-4)-(-6)(5-k)+1(20-4k)=35\\By\ solving\ we\ will\ get\\25-5k=\pm35\\25-5k=35\ and\ 25-5k=-35\\k=-2\ and\ k=12.$

Publicación traducida automáticamente

Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra el área del triángulo con vértices en el punto dado en cada uno de los siguientes:

Pregunta 2. Demuestre que los puntos A (a, b + c), B (b, c + a), C (c, a + b) son colineales.

Pregunta 3. Encuentra los valores de k si el área del triángulo es de 4 unidades cuadradas y los vértices son

(i) (k, 0), (4, 0), (0, 2) (ii)(-2, 0), (0, 4), (0, k)

Pregunta 4. (i) Encuentra la ecuación de la línea que une (1, 2) y (3, 6) usando determinantes. (ii) Encuentre la ecuación de la línea que une (3, 1) y (9, 3) usando determinantes.

Pregunta 5. Si el área del triángulo es de 35 unidades cuadradas con vértices (2, – 6), (5, 4) y (k, 4). Entonces k es (A) 12 (B) –2 (C) –12, –2 (D) 12, –2

Deja una respuesta Cancelar la respuesta

(i) (k, 0), (4, 0), (0, 2)
(ii)(-2, 0), (0, 4), (0, k)

Pregunta 4. (i) Encuentra la ecuación de la línea que une (1, 2) y (3, 6) usando determinantes.
(ii) Encuentre la ecuación de la línea que une (3, 1) y (9, 3) usando determinantes.

Pregunta 5. Si el área del triángulo es de 35 unidades cuadradas con vértices (2, – 6), (5, 4) y (k, 4). Entonces k es
(A) 12 (B) –2 (C) –12, –2 (D) 12, –2