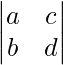Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 4 Determinantes – Ejercicio 4.4

Posted on by Rudeus Greyrat

Escriba los menores y cofactores de los elementos de los siguientes determinantes: 

Pregunta 1. 

(i) 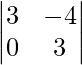\begin{vmatrix}3&-4\\0&3\end{vmatrix}

(ii) 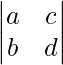\begin{vmatrix}a&c\\b&d\end{vmatrix}

Solución: 

(i) \begin{vmatrix}3&-4\\0&3\end{vmatrix}

Hallar los menores de los elementos del determinante: 

Supongamos que M ij es Menores de elementos a ij

M 11 = Menor de elementos a 11 = 3

M 12 = Menor de elementos a 12 = 0

M 21 = Menor de elementos a 21 = −4

M 22 = Menor de elementos a 22 = 2

Encontrar el cofactor de a ij

Supongamos que el cofactor de a ij es A ij M ij

UN 11 = (−1) 1+1 METRO 11 = (−1) 2 (3) = 3

UN 12 = (−1) 1+2 METRO 12 = (−1) 3 (0) = 0

UN 21 = (−1) 2+1 METRO 21 = (−1) 3 (−4) = 4

UN 22 = (−1) 2+2 METRO 22 = (−1) 4 (2) = 2

(ii) \begin{vmatrix}a&c\\b&d\end{vmatrix}

Hallar los menores de los elementos del determinante:

Supongamos que M ij es Menores de elementos a ij

M 11 = Menor del elemento a 11 = d

M 12 = Menor de elementos a 12 = b

M 21 = Menor de elementos a 21 = c

M 22 = Menor de elementos a 22 = a

Encontrar el cofactor de a ij

Supongamos que el cofactor de a ij es A ij , que es (−1) i+j M ij

UN 11 = (−1) 1+1 METRO 11 = (−1) 2 (re) = re

UN 12 = (−1) 1+2 METRO 12 = (−1) 3 (b) = −b

UN 21 = (−1) 2+1 METRO 21 = (−1) 3 (c) = −c

UN 22 = (−1) 2+2 METRO 22 = (−1) 4 (a) = un

Pregunta 2.

(i)\begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}

(ii)\begin{vmatrix}1&0&4\\3&5&-5\\0&2&2\end{vmatrix}

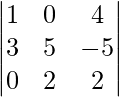
Solución:

(i) \begin{vmatrix}1&0&0\\0&1&0\\0&0&1\end{vmatrix}

Encontremos los Menores y cofactores de los elementos:

Suponga que M ij es menor del elemento a ij y A ij es cofactor de a ij

M 11 = Menor de elementos a 11 = \begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix} = 1 − 0 = 1 y A 11 = 1

M 12 = Menor de elementos a 12 = \begin{vmatrix} 0 & 0\\0 & 1\end{vmatrix} = 0 − 0 = 0 y A 12 = 0

M 13 = Menor de elementos a 13 = \begin{vmatrix} 0 & 1\\0 & 0\end{vmatrix} = 0 − 0 = 0 y A 13 = 0

M 21 = Menor de elementos a 21 = \begin{vmatrix} 0 & 0\\0 & 1\end{vmatrix} = 0 − 0 = 0 y A 21 = 0

M 22 = Menor de elementos a 22 = \begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix} = 1 − 0 = 1 y A 22 = 1

M 23 = Menor de elementos a 23 = \begin{vmatrix} 1 & 0\\0 & 0\end{vmatrix} = 0 − 0 = 0 y A 23 = 0

M 31 = Menor de elementos a 31 = \begin{vmatrix} 0 & 0\\1 & 0\end{vmatrix} = 0 − 0 = 0 y A 31 = 0

M 32 = Menor de elementos a 32 = \begin{vmatrix} 1 & 0\\0 & 0\end{vmatrix} = 0 − 0 = 0 y A 32 = 0

M 33 = Menor de elementos a 33 = \begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix} = 1 − 0 = 1 y A 33 = 1

(ii) \begin{vmatrix}1&0&4\\3&5&-5\\0&2&2\end{vmatrix}

Encontremos los Menores y cofactores de los elementos:

Suponga que M ij es menor del elemento a ij y A ij es cofactor de a ij

M 11 = Menor de elementos a 11 = \begin{vmatrix} 5 & -1\\1 & 2\end{vmatrix} = 10 − (−1) = 11 y A 11 = 11

M 12 = Menor de elementos a 12 = \begin{vmatrix} 3 & -1\\0 & 2\end{vmatrix} = 6 − 0 = 6 y A 12 = −6

M 13 = Menor de elementos a 13 = \begin{vmatrix} 3 & 5\\0 & 1\end{vmatrix} = 3 − 0 = 3 y A 13 = 3

M 21 = Menor de elementos a 21 = \begin{vmatrix} 0 & 4\\1 & 2\end{vmatrix} = 0 − 4 = −4 y A 21 = 4

M 22 = Menor de elementos a 22 = \begin{vmatrix} 1 & 4\\0 & 2\end{vmatrix} = 2 − 0 = 2 y A 22 = 2

M 23 = Menor de elementos a 23 = \begin{vmatrix} 1 & 0\\0 & 1\end{vmatrix} = 1 − 0 = 1 y A 23 = −1

M 31 = Menor de elementos a 31 = \begin{vmatrix} 0 & 4\\5 & -1\end{vmatrix} = 0 − 20 = −20 y A 31 = −20

M 32 = Menor de elementos a 32 = \begin{vmatrix} 1 & 4\\3 & -1\end{vmatrix} = −1 − 12 = −13 y A 32 = 13

M 33 = Menor de elementos a 33 = \begin{vmatrix} 1 & 0\\3 & 5\end{vmatrix} = 5 − 0 = 5 y A 33 = 5

Pregunta 3. Usando cofactores de elementos de la segunda fila, evalúa △?

\bigtriangleup=\begin{vmatrix}5&3&8\\2&0&1\\1&2&3\end{vmatrix}

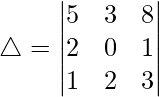
Solución:

Encontrar los cofactores de los elementos de la segunda fila:

A 21 = Cofactor de elementos a 21 = (−1) 2+1  \begin{vmatrix} 3 & 8\\2 & 3\end{vmatrix} = (−1) 3 (9 − 16) = 7

A 22 = Cofactor de elementos a 22 = (−1) 2+2  \begin{vmatrix} 5 & 8\\1 & 3\end{vmatrix} = (−1) 4 (15 − 8) = 7

A 23 = Cofactor de elementos a 23 = (−1) 2+3  \begin{vmatrix} 5 & 3\\1 & 2\end{vmatrix} = (−1) 5 (10 − 3) = 7

Ahora, △ = a 21 A 21 + a 22 A 22 + a 23 A 23 = 14 + 0 − 7 = 7

Pregunta 4. Usando cofactores de elementos de la tercera columna, evalúa △?

\bigtriangleup = \begin{vmatrix}1&x&yz\\1&y&zx\\1&z&xy\end{vmatrix}

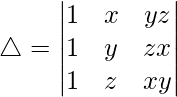
Solución:

Encontrar los cofactores de los elementos de la tercera columna:

A 13 = Cofactor de los elementos a 13 = (−1) 1+3  \begin{vmatrix} 1 & y\\1 & z\end{vmatrix} = (−1) 4 (z − y) = −y

A 23 = Cofactor de los elementos a 23 = (−1) 2+3  \begin{vmatrix} 1 & x\\1 & z\end{vmatrix} = (−1) 5 (z − x) = x − z

A 33 = Cofactor de los elementos a 33 = (−1) 3+3  \begin{vmatrix} 1 & x\\1 & y\end{vmatrix} = (−1) 6 (y − x) = y − x

Ahora, △ = a 13 A 13 + a 23 A 23 + a 33 A 33

= yz (z − y) + zx (x − z) + xy (y − x)

= (yz 2 − y 2 z) + (xy 2 − xz 2 ) + (xz 2 − x 2 y)

= (y − z)[−yz + x(y + z) − x 2 ]

= (y − z)[−yz + x (z − x) + x (z − x)]

= (x − y)(y − x)(z − x)

Pregunta 5. Si  △=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix} y A ij es cofactor de a ij entonces el valor de △ viene dado por:

(A) a 11 A 31 + a 12 A 32 + a 13 A 33

(B) a 11 A 11 + a 12 A 21 + a 13 A 31

(C) a 21 A 11 + a 22 A 12 + a 23 A 13

(D) a 11 A 11 + a 21 A 21 + a 31 A 31

Solución: 

La opción (D) es correcta.

Publicación traducida automáticamente

Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *