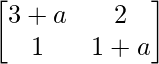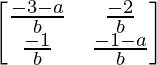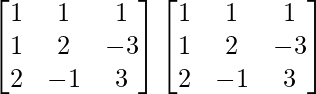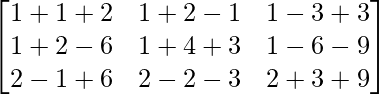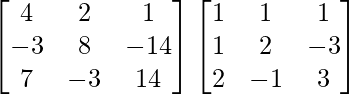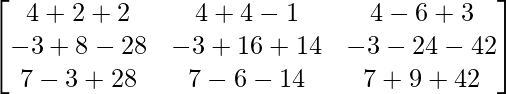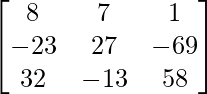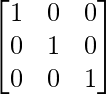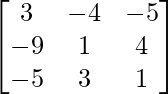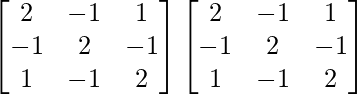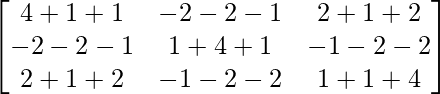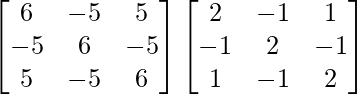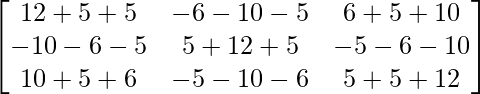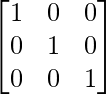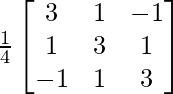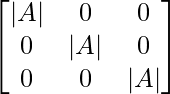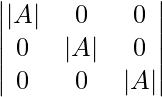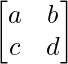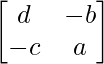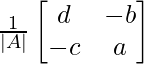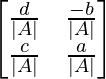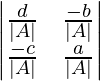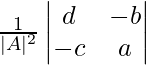Encuentre el adjunto de cada una de las arrays en los ejercicios 1 y 2.
Pregunta 1. 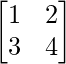
Solución:
un =
A 11 = 4; A12 = -3 ; A 21 = -2; 22 = 1
adj A =
adj A =
Pregunta 2. 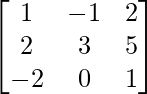
Solución:
un =
un 11 =
UN 11 = 3 – 0 = 3
un 12 =
UN 12 = -(2 + 10) = -12
un 13 =
UN 13 = 0 + 6 = 6
Un 21 =
A 21 = -(-1 – 0) = 1
Un 22 =
UN 22 = 1 + 4 = 5
Un 23 =
A 23 = -(0 – 2) = 2
Un 31 =
A 31 = -5 – 6 = -11
32 = _
A 32 = -(5 – 4) = -1
Un 33 =
UN 33 = 3 + 2 = 5
adj A =
adj A =
Verifique A(adj A) = (adj A)A = |A| I en los ejercicios 3 y 4.
Pregunta 3. 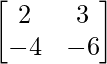
Solución:
|A| = -12 -(-12)
|A| = -12 + 12 = 0
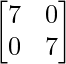
entonces, |A|*I = 0 *
|A|*I =
……… (1)
Ahora, para adjunto de A
Un 11 = -6
un 12 = 4
Un 21 = -3
22 = 2
adj A =
adj A =
Ahora, A(adj A) =
A(adj A) =
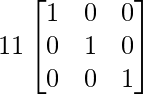
[Tex]\begin{bmatrix} 11& 0 &0 \\ 0 & 11 &0 \\ 0 & 0 & 11 \end{bmatrix}[/Tex]
A(adj A) =
…………(2)
Ahora, (adj. A)A =
(adj. A)A =
(adj. A)A =
…………….(3)
A partir de la ecuación (1), (2) y (3), puede ver que A(adj A) = (adj A)A = |A|I
Pregunta 4. 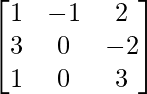
Solución:
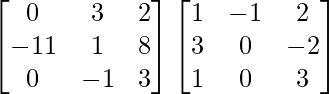
un =
|A| = 1(0 – 0) + 1(9 + 2) + 2(0 – 0)
|A| = 11
|A| * yo =
|A| * yo =
Ahora, para adjunto de A
un 11 = 0
UN 12 = -(9 + 2) = -11
un 13 = 0
A 21 = -(-3 – 0) = 3
UN 22 = 3 – 2 = 1
A 23 = -(0 + 1) = -1
UN 31 = 2 – 0 = 2
UN 32 = -(-2 – 6) = 8
UN 33 = 0 + 3 = 3
adj A =
Ahora,
A(adjA) =
A(adj. A) =
A(adj. A) =
También,
(adj. A).A =
(adj. A).A =
(adj. A).A =
Desde arriba, se puede ver,
A(adj A) = (adj A)A = yo
Encuentre la inversa de cada una de las arrays (si existe) dadas en los ejercicios 5 a 11.
Pregunta 5. 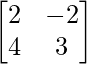
Solución:
|A| = 6 – (-8) = 14
|A| ≠ 0, por lo que existe inversa.
UN 11 = 3
un 12 = 2
Un 21 = -4
22 = 2
adj A =
A -1 = (adj. A)/|A|
A -1 =
Pregunta 6. 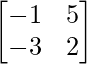
Solución:
un =
|A| = -2 + 15 = 13 ≠ 0
Por lo tanto, existe inversa.
UN 11 = 2
un 12 = 3
Un 21 = -5
Un 22 = -1
adj A =
A -1 = (adj. A)/|A|
A -1 =
Pregunta 7. 
Solución:
un =
|A| = 1(10 – 0) – 2(0 – 0) + 3(0 – 0) = 10
para adjetivo A
UN 11 = 10 – 0 = 0
A12 = – ( 0 – 0) = 0
UN 13 = 0 – 0 = 0
A 21 = -(10 – 0) = -10
UN 22 = 5 – 0 = 5
A 23 = -(0 – 0) = 0
UN 31 = 8 – 6 = 2
A 32 = -(4 – 0) = -4
UN 33 = 2 – 0 = 2
adj A =
A -1 = (adj. A)/|A|
A -1 =
pregunta 8 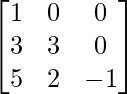
Solución:
un =
|A| = 1(-3 – 0) – 0 + 0 = -3 ≠ 0
Por lo tanto, existe inversa.
para adjetivo A
A 11 = -3 – 0 = -3
UN 12 = -(-3 – 0) = 3
A 13 = 6 – 15 = -9
A 21 = -(0 – 0) = 0
A 22 = -1 – 0 = -1
A 23 = -(2 – 0) = -2
UN 31 = 0 – 0 = 0
A 32 = -(0 – 0) = 0
UN 33 = 3 – 0 = 3
adj A =
A -1 = (adj. A)/|A|
A -1 =
Pregunta 9. 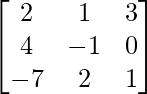
Solución:
un =
|A| = 2(-1 – 0) – 1(4 – 0) + 3(8 – 7) = -3 ≠ 0
Por lo tanto, existe inversa.
para adjetivo A
A 11 = -1 – 0 = -1
A 12 = -(4 – 0) = -4
UN 13 = 8 – 7 = 1
A 21 = -(1 – 6) = 5
22 = 2 + 21 = 23
A 23 = -(4 + 7) = -11
UN 31 = 0 + 3 = 3
UN 32 = -(0 – 12) = 12
A 33 = -2 – 4 = -6
adj A =
A -1 = (adj. A)/|A|
A -1 =
Pregunta 10. 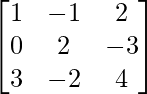
Solución:
un =
|A| = 1(8 – 6) – 0 + 3(3 – 4) = -1
Ahora para adj A
A 11 = 8 – 6 = 2
A12 = – ( 0 + 9) = -9
A 13 = 0 – 6 = -6
A 21 = -(-4 + 4) =0
A 22 = 4 – 6 = -2
A 23 = -(-2 + 3) = -1
A 31 = 3 – 4 = -1
UN 32 = -(-3 – 0) = 3
UN 33 = 2 – 0 = 2
adj A =
A -1 = (adj. A)/|A|
A -1 =
A -1 =
Pregunta 11. 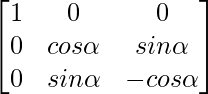
Solución:
un =
|A| = 1(-cos2 – sen2) = -1
Ahora,
A 11 = -cos2 – sen2 = -1
un 12 = 0
un 13 = 0
21 = 0
A 22 = -cos
A 23 = -sen
31 = 0
A 32 = -sin
A 33 = porque
adj A =
A -1 = (adj. A)/|A|
A -1 =
A -1 =
Pregunta 12. Sean A = 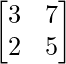 y B =
y B = 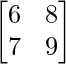 , verifica que (AB) – 1 = B – 1 A – 1
, verifica que (AB) – 1 = B – 1 A – 1
Solución:
un =
|A| = 15 – 14 = 1
UN 11 = 5
Un 12 = -2
A 21 = -7
22 = 3
A -1 = (adj. A)/|A|
A -1 =
B =
|B| = 54 – 56 = -2
adj B =
B -1 = (adj B)/|B|
B -1 =
B -1 =
Ahora,
B -1 A -1 =
B -1 A -1 =
B -1 A -1 =
Ahora AB =
AB =
AB =
|AB| = 67 * 61 – 87 * 47 = -2
adj (AB) =
(AB) -1 = (adj. AB)/|AB|
(AB) -1 =
(AB) -1 =
Desde arriba, puedes ver que (AB) -1 = B -1 A -1 .
Por lo tanto, está probado.
Pregunta 13. A = 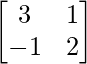 , demuestre que A 2 – 5A + 7I = O. Por lo tanto, encuentre A -1 .
, demuestre que A 2 – 5A + 7I = O. Por lo tanto, encuentre A -1 .
Solución:
un =
un 2 =
un 2 =
un 2 =
Entonces, A 2 – 5A + 7I
=
– 5
+ 7
=
–
+
=
=O
Por lo tanto, A 2 – 5A + 7I = O
Se puede escribir como
AA-5A = -7I
Multiplicando por A -1 en ambos lados
AA(A -1 ) – 5AA -1 = 7IA -1
A(AA -1 ) – 5I = -7A -1
IA – 5I = -7A -1
A -1 = -(A – 5I)/7
A -1 = 1/7 (
–
)
A -1 =
Pregunta 14. Para la array A = 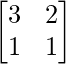 , encuentre los números a y b tales que A2 + aA + bI = O.
, encuentre los números a y b tales que A2 + aA + bI = O.
Solución:
un =
un 2 =
un 2 =
A2 =
Ahora,
A 2 – aA + bI = O
Multiplicando por A -1 en ambos lados
(AA)A -1 + aAA -1 + bIA -1 = O
A(AA -1 ) + aI + b(IA -1 ) = O
AI + aI + bA -1 = O
A + aI = -bA -1
A -1 = -(A + aI)/b
Ahora,
A -1 = (adj. A)/|A|
A -1 =
Ahora,
= -1/b
=
Al comparar elementos obtendrás
-1/b = -1
segundo = 1
(-3 – a)/b = 1
-3 – un = 1
un = -4
Por lo tanto, a = -4 y b = 1
Pregunta 15. A = 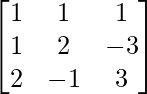 , demuestre que A 3 – 6A 2 + 5A + 11I = O. Por lo tanto, encuentre A -1
, demuestre que A 3 – 6A 2 + 5A + 11I = O. Por lo tanto, encuentre A -1
Solución:
un =
un 2 =
un 2 =
un 2 =
A 3 = A 2 .A
un 3 =
un 3 =
un 3 =
A 3 – 6A 2 + 5A + 11I
– 6
+ 5
+ 11
=
–
+
+
=
=O
Por lo tanto, A 3 – 6A 2 + 5A + 11I = O
Ahora,
A 3 – 6A 2 + 5A + 11I = O
(AAA)A -1 – 6(AA)A -1 + 5(AA -1 ) + 11IA -1 = O
AA(AA -1 ) – 6A(AA -1 ) + 5(AA -1 ) = -11(IA -1 )
UN 2 – 6A + 5I = -11 UN -1
A -1 = -1/11(A2 – 6A + 5I) ………….(1)
Ahora, A 2 – 6A + 5I
=
– 6
+ 5
=
–
+
=
De la ecuación (1) tienes
A -1 = -1/11
Pregunta 16. A = 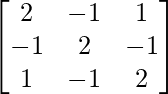 , verifique que A 3 – 6A 2 + 9A – 4I = O y por lo tanto fin A -1 .
, verifique que A 3 – 6A 2 + 9A – 4I = O y por lo tanto fin A -1 .
Solución:
un =
un 2 =
un 2 =
un 2 =
A 3 = A 2 .A
un 3 =
un 3 =
un 3 =
Ahora,
A 3 – 6A 2 + 9A – 4I
– 6
+ 9
– 4
=
–
+
–
=
–
=
=O
Entonces, A 3 – 6A 2 + 9A – 4I = O
Ahora,
A 3 – 6A 2 + 9A – 4I = O
Multiplicando por A -1 en ambos lados
(AAA)A -1 – 6(AA)A -1 + 9AA -1 – 4IA -1 = O
AA(AA -1 ) – 6A(AA -1 ) + 9(AA -1 ) = 4(IA -1 )
IAA – 6AI +9I = 4A -1
A 2 – 6A + 9I = 4A -1
A -1 = 1/4(A2 – 6A + 9I) ……….(1)
A 2 – 6A + 9I
=
– 6
+ 9
=
De la ecuación (1), tienes
A -1 =
Pregunta 17. Sea A una array no singular de orden 3 * 3. Entonces |adj A| es igual a
(A) |A| (B) |A| 2 (C) |A| 3 (D) 3|A|
Solución:
Sabes,
(adj. A)A = |A|I
(adj. A)A =
|(adj A)A| =
|(adj A)A| = |A| 3
|(adj A)A| = |A| 3 yo
|adj A| = |A| 3
Por lo tanto, la opción B es correcta.
Pregunta 18. Si A es una array invertible de orden 2, entonces det(A -1 ) es igual a
(A) det(A) (B) 1/(det A) (C) 1 (D) 0
Solución:
Como A es una array invertible, entonces A -1 existe.
Y A -1 = (adj A)/|A|
Supongamos que una array de 2 orden es A =
Entonces |A| = anuncio – ac
y adj A =
A -1 = (adj. A)/|A|
A -1 =
A -1 =
|A -1 | =
|A -1 | =
|A -1 | = (ad – ac)/|A| 2
|A -1 | = |A|/|A| 2
|A -1 | = 1/|A|
det(A -1 ) = 1/(det A)
Por lo tanto, la opción B es correcta.
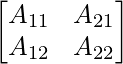
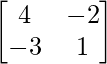
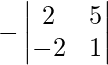
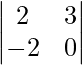
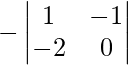

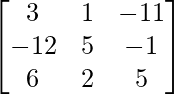

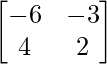
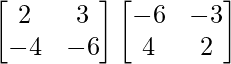
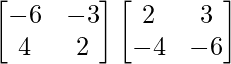
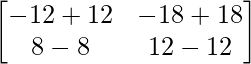

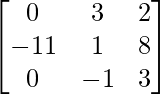
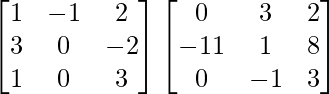
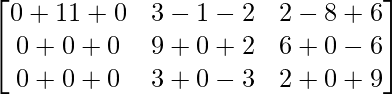
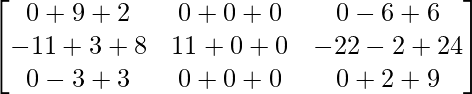
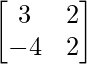
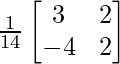
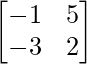
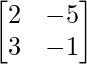
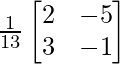
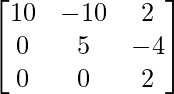
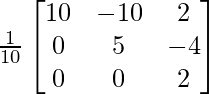
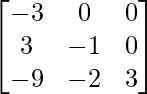
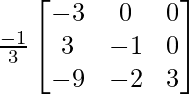
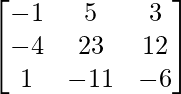
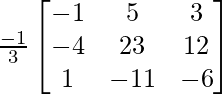
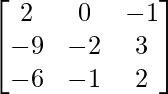
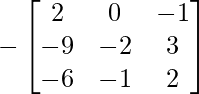
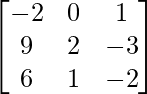
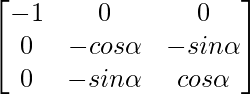
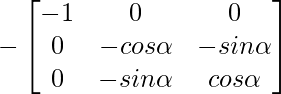
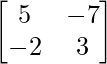
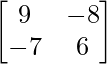
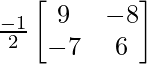
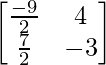
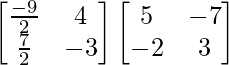
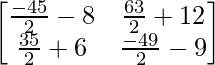
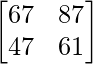
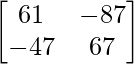
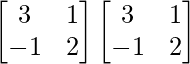
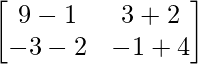


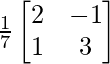
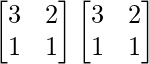
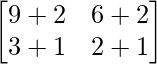
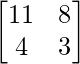
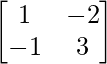
![Rendered by QuickLaTeX.com \begin{bmatrix} 1 &-2 \\ -1& 3 \end{bmatrix} = -1/b[\begin{bmatrix} 3 &2 \\ 1& 1 \end{bmatrix} + \begin{bmatrix} a &0 \\ 0& a \end{bmatrix}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-78d7045dbf4047f4d70a97e32e8789ef_l3.png)