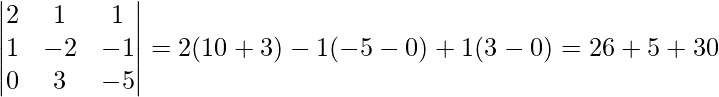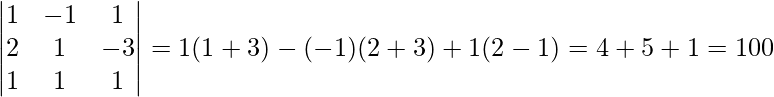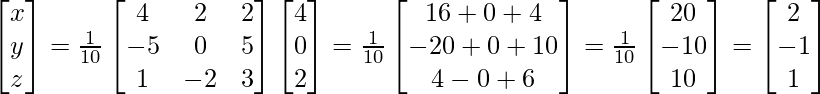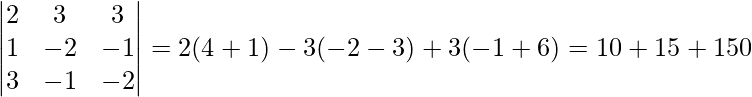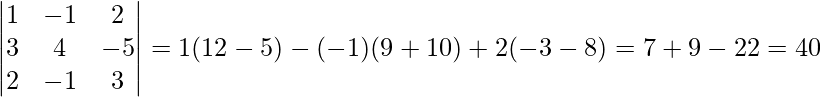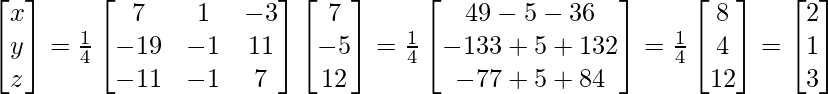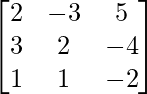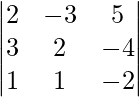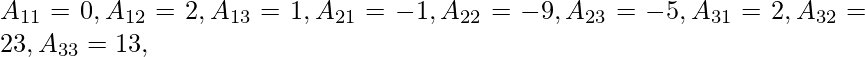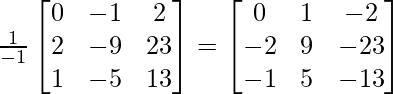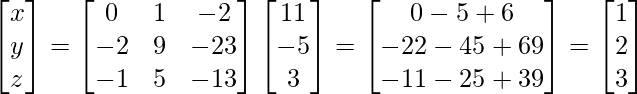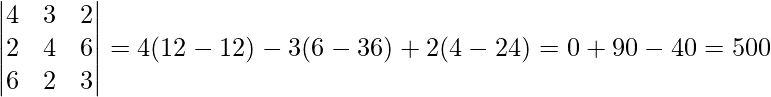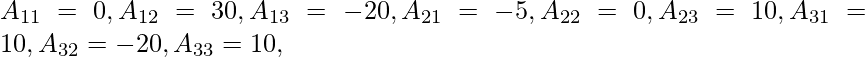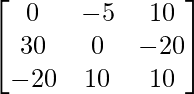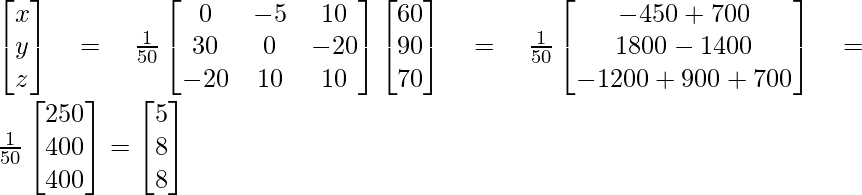Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 4 Determinantes – Ejercicio 4.6 | conjunto 2

Posted on by Rudeus Greyrat

Capítulo 4 Determinantes – Ejercicio 4.6 | Serie 1

Pregunta 11. 2x + y + z = 1 

                               x-2y-z = 3/2

                               3y – 5z = 9 

Solución:

La forma matricial de la ecuación dada es AX = B

es decir\begin{bmatrix}2 & 1 & 1\\1 & -2 & -1\\0 & 3 & -5\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}1\\3/2\\9\end{bmatrix}

∴ |A| =\begin{vmatrix}2 & 1 & 1\\1 & -2 & -1\\0 & 3 & -5\end{vmatrix}=2(10+3)-1(-5-0)+1(3-0)=26+5+3≠0

∴ La solución es única.

Ahora, X = A -1 B =  \frac{1}{|A|} (adj.A)B

\begin{bmatrix}x\\y\\z\end{bmatrix}=\frac{1}{34}\begin{bmatrix}13 & 8 & 1\\5 & -10 & 3\\3 & -6 & -5\end{bmatrix}\begin{bmatrix}1\\3/2\\ 9\end{bmatrix} =\frac{1}{34}\begin{bmatrix}13+12+9\\5-15+27\\3-9-45\end{bmatrix}=\frac{1}{34}\begin{bmatrix}34\\17\\-51\end{bmatrix}=\begin{bmatrix}1\\1/2\\-3/2\end{bmatrix}

Por lo tanto, x=1, y=1/2, z=3/2

Pregunta 12. x – y + z = 4

                                2x + y – 3z = 0

                                x + y + z = 2

Solución:

La forma matricial de la ecuación dada es AX = B

es decir\begin{bmatrix}1 & -1 & 1\\2 & 1 & -3\\1 & 1 & 1\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}4\\0\\2\end{bmatrix}

∴ |A| =\begin{vmatrix}1 & -1 & 1\\2 & 1 & -3\\1 & 1 & 1\end{vmatrix}=1(1+3)-(-1)(2+3)+1(2-1)=4+5+1=10≠0

∴ La solución es única.

Ahora, X = A -1 B = \frac{1}{|A|}  (adj.A)B

\begin{bmatrix}x\\y\\z\end{bmatrix}=\frac{1}{10}\begin{bmatrix}4 & 2 & 2\\-5 & 0 & 5\\1 & -2 & 3\end{bmatrix}\begin{bmatrix}4\\0\\ 2\end{bmatrix} =\frac{1}{10}\begin{bmatrix}16+0+4\\-20+0+10\\4-0+6\end{bmatrix}=\frac{1}{10}\begin{bmatrix}20\\-10\\10\end{bmatrix}=\begin{bmatrix}2\\-1\\ 1\end{bmatrix}

Por lo tanto, x = 2, y = -1, z = 1

Pregunta 13. 2x + 3y +3 z = 5 

                               x – 2y + z = – 4 

                               3x-y-2z = 3

Solución:

La forma matricial de la ecuación dada es AX = B

es decir\begin{bmatrix}2 & 3 & 3\\1 & -2 & -1\\3 & -1 & -2\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}5\\-4\\3\end{bmatrix}

∴ |A| =\begin{vmatrix}2 & 3 & 3\\1 & -2 & -1\\3 & -1 & -2\end{vmatrix}=2(4+1)-3(-2-3)+3(-1+6)=10+15+15≠0

∴ La solución es única.

Ahora, X = A -1 B =  \frac{1}{|A|} (adj.A)B

\begin{bmatrix}x\\y\\z\end{bmatrix}=\frac{1}{40}\begin{bmatrix}5 & 3 & 9\\5 & -13 & 1\\5 & 11 & -7\end{bmatrix}\begin{bmatrix}5\\-4\\ 3\end{bmatrix} =\frac{1}{10}\begin{bmatrix}25-12+27\\25+52+3\\25-44-21\end{bmatrix}=\frac{1}{10}\begin{bmatrix}40\\80\\-40\end{bmatrix}=\begin{bmatrix}1\\2\\ -1\end{bmatrix}

Por lo tanto, x = 1, y = 2, z = -1

Pregunta 14. x – y + 2z = 7

                               3x + 4y – 5z = – 5

                               2x – y + 3z = 12

Solución:

La forma matricial de la ecuación dada es AX = B

es decir\begin{bmatrix}1 & -1 & 2\\3 & 4 & -5\\2 & -1 & 3\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}7\\-5\\12\end{bmatrix}

∴ |A| =\begin{vmatrix}1 & -1 & 2\\3 & 4 & -5\\2 & -1 & 3\end{vmatrix}=1(12-5)-(-1)(9+10)+2(-3-8)=7+9-22=4≠0

∴ La solución es única.

Ahora, X = A -1 B = \frac{1}{|A|}  (adj.A)B

\begin{bmatrix}x\\y\\z\end{bmatrix}=\frac{1}{4}\begin{bmatrix}7 & 1 & -3\\-19 & -1 & 11\\-11 & -1 & 7\end{bmatrix}\begin{bmatrix}7\\-5\\ 12\end{bmatrix} =\frac{1}{4}\begin{bmatrix}49-5-36\\-133+5+132\\-77+5+84\end{bmatrix}=\frac{1}{4}\begin{bmatrix}8\\4\\12\end{bmatrix}=\begin{bmatrix}2\\1\\ 3\end{bmatrix}

Por lo tanto, x = 2, y = 1, z = 3

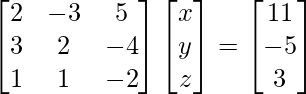
Pregunta 15. Si A= 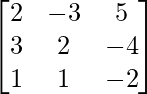\begin{bmatrix}2 & -3 & 5\\3 & 2 & -4\\1 & 1 & -2\end{bmatrix} , encuentre A–1. Usando A–1 resuelve el sistema de ecuaciones 

2x – 3y + 5z = 11

3x + 2y – 4z = – 5

x + y – 2z = – 3

Solución:

Dado: A=\begin{bmatrix}2 & -3 & 5\\3 & 2 & -4\\1 & 1 & -2\end{bmatrix}

Ahora, |A|= \begin{vmatrix}2 & -3 & 5\\3 & 2 & -4\\1 & 1 & -2\end{vmatrix}

∴ |A|= 2(-4+4)-(-3)(-6+4)+5(3-2)=0-6+5= -1≠0

Significa que A -1 existe.

Y A -1 = \frac{1}{|A|} (adj.A)……(1)

Ahora, A_{11}=0,A _{12}=2,A _{13}=1, A _{21}=-1,A _{22}=-9,A _{23}=-5, A _{31}=2,A _{32}=23,A _{33}=13,

∴ adj. un =\begin{bmatrix}0 & -1 & 2\\2 & -9 & 23\\1 & -5 & 13\end{bmatrix}

De la ec. (1),

A – 1 =\frac{1}{-1}\begin{bmatrix}0 & -1 & 2\\2 & -9 & 23\\1 & -5 & 13\end{bmatrix}=\begin{bmatrix}0 & 1 & -2\\-2 & 9 & -23\\-1 & 5 & -13\end{bmatrix}

Ahora, la forma matricial de la ecuación dada es AX = B

es decir\begin{bmatrix}2 & -3 & 5\\3 & 2 & -4\\1 & 1 & -2\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}11\\-5\\3\end{bmatrix}

∵ La solución es única.

∴X= A -1B

⇒\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}0 & 1 & -2\\-2 & 9 & -23\\-1 & 5 & -13\end{bmatrix}\begin{bmatrix}11\\-5\\3\end{bmatrix} =\begin{bmatrix}0-5+6\\-22-45+69\\-11-25+39\end{bmatrix} =\begin{bmatrix}1\\2\\3\end{bmatrix}

Por lo tanto, x = 1, y = 2, z = 3

Pregunta 16. El costo de 4 kg de cebolla, 3 kg de trigo y 2 kg de arroz es de 60 rupias. El costo de 2 kg de cebolla, 4 kg de trigo y 6 kg de arroz es de 90 rupias. El costo de 6 kg de cebolla, 2 kg de trigo y 3 kg de arroz es de 70 rupias. Encuentre el costo de cada artículo por kg por método matricial.

Solución:

Sean Rs x, Rs y, Rs z por kg los precios de la cebolla, el trigo y el arroz respectivamente.

ATQ

4x+3y+2z=60

2x+4y+6z=90

6x+2y+3z=70

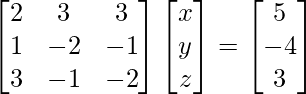
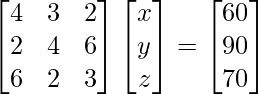
La forma matricial de la ecuación es AX = B

donde, A= \begin{bmatrix}4 & 3 & 2\\2 & 4 & 6\\6 & 2 & 3\end{bmatrix} ,B= \begin{bmatrix}60\\90\\70\end{bmatrix} y X=\begin{bmatrix}x\\y\\z\end{bmatrix}

=> \begin{bmatrix}4 & 3 & 2\\2 & 4 & 6\\6 & 2 & 3\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}60\\90\\70\end{bmatrix}

Ahora, |A|=\begin{vmatrix}4 & 3 & 2\\2 & 4 & 6\\6 & 2 & 3\end{vmatrix}=4(12-12)-3(6-36)+2(4-24)=0+90-40=50 ≠0

∴ La solución es única

Ahora, X=A -1 B= \frac{1}{|A|} (adj. A)B……(1)

Ahora,  A_{11}=0,A _{12}=30,A _{13}=-20, A _{21}=-5,A _{22}=0,A _{23}=10, A _{31}=10,A _{32}=-20,A _{33}=10,

∴ (adj.A)= \begin{bmatrix}0 & -5 & 10\\30 & 0 & -20\\-20 & 10 & 10\end{bmatrix}

De la ecuación n . (1)

\begin{bmatrix}x\\y\\z\end{bmatrix}=\frac{1}{50}\begin{bmatrix}0 & -5 & 10\\30 & 0 & -20\\-20 & 10 & 10\end{bmatrix}\begin{bmatrix}60\\90\\70\end{bmatrix} =\frac{1}{50}\begin{bmatrix}-450+700\\1800-1400\\-1200+900+700\end{bmatrix}=\frac{1}{50}\begin{bmatrix}250\\400\\400\end{bmatrix} =\begin{bmatrix}5\\8\\8\end{bmatrix}

Por lo tanto, x = 5, y = 8, z = 8

Por lo tanto, el costo de la cebolla, el trigo y el arroz es de Rs. 5, 8 rupias y 8 rupias por kg.

Publicación traducida automáticamente

Artículo escrito por kavyagupta0098 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *