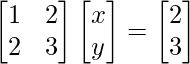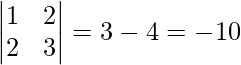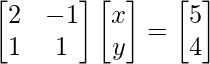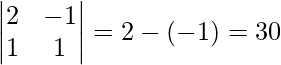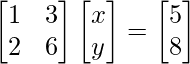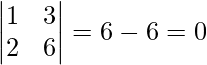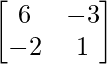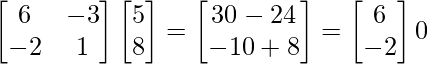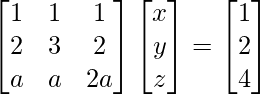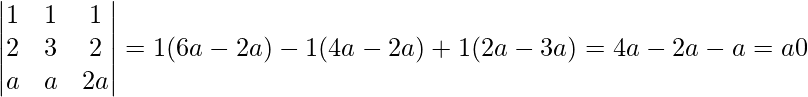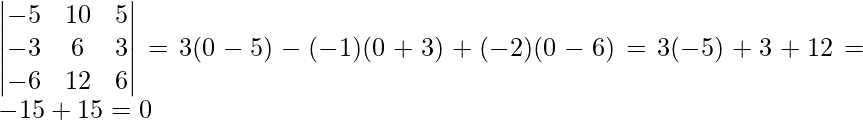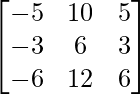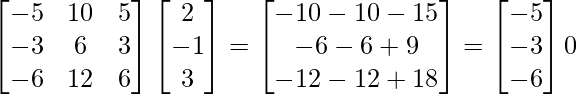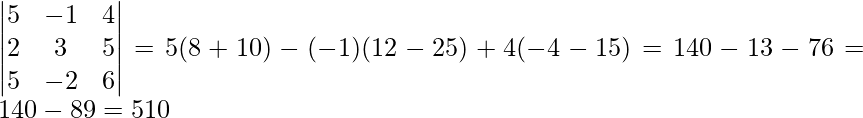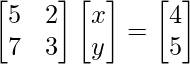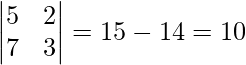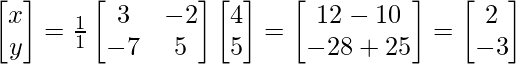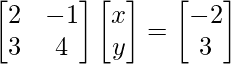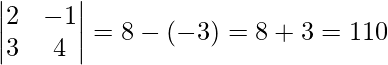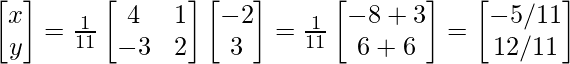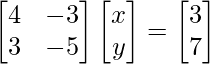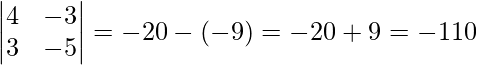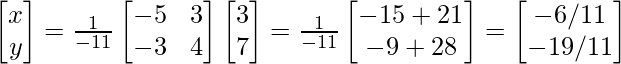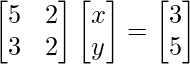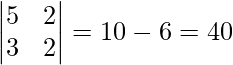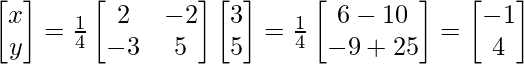Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 4 Determinantes – Ejercicio 4.6 | Serie 1

Posted on by Rudeus Greyrat

Examine la consistencia del sistema de ecuaciones en los ejercicios 1 a 6.

Pregunta 1. x + 2y = 2

                            2x + 3y = 3

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A = \begin{bmatrix}1 & 2 \\2 & 3 \\\end{bmatrix}  , B =  \begin{bmatrix}2 \\3 \\\end{bmatrix}   y, X = \begin{bmatrix}x\\y\\\end{bmatrix}

∴  \begin{bmatrix}1 & 2 \\2 & 3 \\\end{bmatrix}\begin{bmatrix}x\\y\\\end{bmatrix}=\begin{bmatrix}2 \\3 \\\end{bmatrix}

Ahora, |A| = {\begin{vmatrix}1&2\\2&3\end{vmatrix}} = 3-4 = -1 ≠ 0

∵ Existe inversa de array, única solución.

∴ El sistema de ecuaciones es consistente.

Pregunta 2. 2x – y = 5 

                            x + y = 4

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A = \begin{bmatrix}2 & -1 \\1 & 1 \\\end{bmatrix} , B = \begin{bmatrix}5 \\4 \\\end{bmatrix}   y, X =\begin{bmatrix}x\\y\\\end{bmatrix}

∴\begin{bmatrix}2 & -1 \\1 & 1 \\\end{bmatrix}\begin{bmatrix}x\\y\\\end{bmatrix}=\begin{bmatrix}5 \\4 \\\end{bmatrix}

Ahora, |A| ={\begin{vmatrix}2&-1\\1&1\end{vmatrix}} = 2-(-1) = 3 ≠ 0

∵ Existe inversa de array, única solución.

∴ El sistema de ecuaciones es consistente.

Pregunta 3. x + 3y = 5 

                            2x + 6y = 8

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A = \begin{bmatrix}1 &3 \\2 & 6 \\\end{bmatrix} , B =  \begin{bmatrix}5 \\8 \\\end{bmatrix}  y, X =\begin{bmatrix}x\\y\\\end{bmatrix}

∴ \begin{bmatrix}1 & 3 \\2 & 6 \\\end{bmatrix}\begin{bmatrix}x\\y\\\end{bmatrix}=\begin{bmatrix}5 \\8 \\\end{bmatrix}

Ahora, |A| ={\begin{vmatrix}1&3\\2&6\end{vmatrix}} = 6-6=0

Y, adj. un =\begin{bmatrix}6& -3 \\-2& 1 \\\end{bmatrix}

∴ (adj. A) B = \begin{bmatrix}6 & -3 \\-2 & 1 \\\end{bmatrix}\begin{bmatrix}5\\8\\\end{bmatrix}=\begin{bmatrix}30-24 \\-10+8 \\\end{bmatrix}=\begin{bmatrix}6\\-2\\\end{bmatrix} ≠0

∵ No tienen solución común.

∴ El sistema de ecuaciones es inconsistente.

Pregunta 4. x + y + z = 1 

                            2x + 3y + 2z = 2 

                            hacha + ay + 2az = 4

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A = \begin{bmatrix}1 & 1 & 1\\2 & 3 & 2\\a & a & 2a\end{bmatrix} , B = \begin{bmatrix}1\\2\\4\end{bmatrix} y, X =\begin{bmatrix}x\\y\\z\end{bmatrix}

∴  \begin{bmatrix}1 & 1 & 1\\2 & 3 & 2\\a & a & 2a\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}1\\2\\4\end{bmatrix}

Ahora, |A| = {\begin{vmatrix}1&1&1\\2&3&2\\a&a&2a\end{vmatrix}} = 1(6a-2a)-1(4a-2a)+1(2a-3a)=4a-2a-a=a≠0

∵ Existe inversa de array, única solución.

∴ El sistema de ecuaciones es consistente.

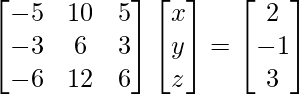
Pregunta 5. 3x – y – 2z = 2 

                            2y – z = -1 

                            3x – 5y = 3 

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A = {\begin{bmatrix}-5&10&5\\-3&6&3\\-6&12&6\end{bmatrix}} , B= \begin{bmatrix}2\\-1\\3\end{bmatrix} y, X =\begin{bmatrix}x\\y\\z\end{bmatrix}

∴{\begin{bmatrix}-5&10&5\\-3&6&3\\-6&12&6\end{bmatrix}}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}2\\-1\\3\end{bmatrix}

Ahora, |A| ={\begin{vmatrix}-5&10&5\\-3&6&3\\-6&12&6\end{vmatrix}} = 3(0-5)-(-1)(0+3)+(-2)(0-6)=3(-5)+3+12=-15+15=0

Y, adj. un =\begin{bmatrix}-5 & 10 & 5\\-3 & 6 & 3\\-6 & 12 & 6\end{bmatrix}

∴ (adj. A) B =\begin{bmatrix}-5 & 10 & 5\\-3 & 6 & 3\\-6 & 12 & 6\end{bmatrix}\begin{bmatrix}2\\-1\\3\end{bmatrix}=\begin{bmatrix}-10-10-15\\-6-6+9 \\-12-12+18\end{bmatrix}=\begin{bmatrix}-5\\-3\\-6\end{bmatrix} ≠0

∴ El sistema de ecuaciones es inconsistente.

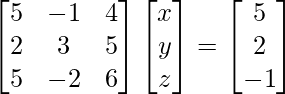
Pregunta 6. 5x – y + 4z = 5

                            2x + 3y + 5z = 2 

                             5x – 2y + 6z = –1

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A = \begin{bmatrix}5 & -1 & 4\\2 & 3 & 5\\5 & -2 & 6\end{bmatrix} , B =  \begin{bmatrix}5\\2\\-1\end{bmatrix} y, X=\begin{bmatrix}x\\y\\z\end{bmatrix}

∴\begin{bmatrix}5 & -1 & 4\\2 & 3 & 5\\5 & -2 & 6\end{bmatrix}\begin{bmatrix}x\\y\\z\end{bmatrix}=\begin{bmatrix}5\\2\\-1\end{bmatrix}

Ahora, |A| =\begin{vmatrix}5 & -1 & 4\\2 & 3 & 5\\5 & -2 & 6\end{vmatrix}=5(8+10)-(-1)(12-25)+4(-4-15)=140-13-76=140-89=51≠0

∵ Existe inversa de array, única solución.

∴ El sistema de ecuaciones es consistente.

Resolver sistemas de ecuaciones lineales, usando el método matricial, en los Ejercicios 7 al 14.

Pregunta 7. 5x + 2y = 4 

                            7x + 3y = 5

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A= \begin{bmatrix}5 &2 \\7 & 3 \\\end{bmatrix} , B= \begin{bmatrix}4 \\5 \\\end{bmatrix} , X=\begin{bmatrix}x\\y\\\end{bmatrix}

∴\begin{bmatrix}5 &2 \\7 & 3 \\\end{bmatrix}\begin{bmatrix}x\\y\\\end{bmatrix}=\begin{bmatrix}4 \\5 \\\end{bmatrix}

Ahora, |A|=\begin{vmatrix}5 &2 \\7 & 3 \\\end{vmatrix}=15-14=1 ≠0

∴ Solución única

Ahora, X = A -1 B = \frac{1}{|A|} (adj.A)B

\begin{bmatrix}x\\y\\\end{bmatrix}=\frac{1}{1}\begin{bmatrix}3&-2\\-7&5\\\end{bmatrix}\begin{bmatrix}4\\5\\\end{bmatrix}=\begin{bmatrix}12-10 \\-28+25 \\\end{bmatrix}=\begin{bmatrix}2 \\- 3 \\\end{bmatrix}

Por lo tanto, x=2 y y=-3

Pregunta 8. 2x – y = -2 

                            3x + 4y = 3

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A= \begin{bmatrix}2 &-1 \\3 & 4 \\\end{bmatrix} , B= \begin{bmatrix}-2 \\3 \\\end{bmatrix} , X=\begin{bmatrix}x\\y\\\end{bmatrix}

∴\begin{bmatrix}2 &-1 \\3 & 4 \\\end{bmatrix}\begin{bmatrix}x\\y\\\end{bmatrix}=\begin{bmatrix}-2 \\3 \\\end{bmatrix}

Ahora, |A|=\begin{vmatrix}2 &-1 \\3 & 4 \\\end{vmatrix}=8-(-3)=8+3=11≠0

∴ Solución única

Ahora, X = A -1 B  \frac{1}{|A|} (adj.A)B

\begin{bmatrix}x\\y\\\end{bmatrix}=\frac{1}{11}\begin{bmatrix}4&1\\-3&2\\\end{bmatrix}\begin{bmatrix}-2\\3\\\end{bmatrix}=\frac{1}{11}\begin{bmatrix}-8+3 \\6+6 \\\end{bmatrix}=\begin{bmatrix}-5/11 \\12/11 \\\end{bmatrix}

Por lo tanto, x=-5/11 y y=12/11

Pregunta 9. 4x – 3y = 3

                            3x – 5y = 7

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A= \begin{bmatrix}4 &-3 \\3 & -5 \\\end{bmatrix} , B= \begin{bmatrix}3 \\7 \\\end{bmatrix} , X=\begin{bmatrix}x\\y\\\end{bmatrix}

∴\begin{bmatrix}4 &-3 \\3 & -5 \\\end{bmatrix}\begin{bmatrix}x\\y\\\end{bmatrix}=\begin{bmatrix}3 \\7 \\\end{bmatrix}

Ahora, |A|=\begin{vmatrix}4 &-3 \\3 & -5 \\\end{vmatrix}=-20-(-9)=-20+9=-11≠0

∴ Solución única \begin{vmatrix}4 &-3 \\3 & -5 \\\end{vmatrix}=-20-(-9)=-20+9=-11≠0 n

Ahora, X =A -1 B  \frac{1}{|A|} A(adj.A)B

\begin{bmatrix}x\\y\\\end{bmatrix}=\frac{1}{-11}\begin{bmatrix}-5&3\\-3&4\\\end{bmatrix}\begin{bmatrix}3\\7\\\end{bmatrix}=\frac{1}{-11}\begin{bmatrix}-15+21 \\-9+28 \\\end{bmatrix}=\begin{bmatrix}-6/11 \\-19/11 \\\end{bmatrix}

Por tanto, x= -6/11 y y= -19/11

Pregunta 10. 5x + 2y = 3 

                               3x + 2y = 5

Solución:

La forma matricial de las ecuaciones dadas es AX = B

donde, A= \begin{bmatrix}5 &2 \\3 & 2 \\\end{bmatrix} , B= \begin{bmatrix}3 \\5 \\\end{bmatrix} , X=\begin{bmatrix}x\\y\\\end{bmatrix}

∴\begin{bmatrix}5 &2 \\3 & 2 \\\end{bmatrix}\begin{bmatrix}x\\y\\\end{bmatrix}=\begin{bmatrix}3 \\5 \\\end{bmatrix}

Ahora, |A|=\begin{vmatrix}5 &2 \\3 & 2 \\\end{vmatrix}=10-6=4≠0

∴ Solución única

Ahora, X = A -1 B \frac{1}{|A|} A(adj.A)B

\begin{bmatrix}x\\y\\\end{bmatrix}=\frac{1}{4}\begin{bmatrix}2&-2\\-3&5\\\end{bmatrix}\begin{bmatrix}3\\5\\\end{bmatrix}=\frac{1}{4}\begin{bmatrix}6-10 \\-9+25 \\\end{bmatrix}=\begin{bmatrix}-1 \\4 \\\end{bmatrix}

Por lo tanto, x= -1 y y= 4

Capítulo 4 Determinantes – Ejercicio 4.6 | conjunto 2

Publicación traducida automáticamente

Artículo escrito por kavyagupta0098 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *