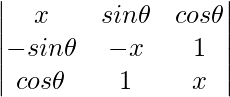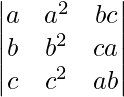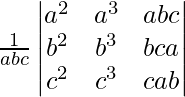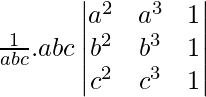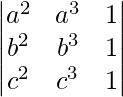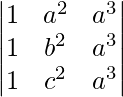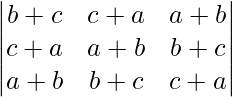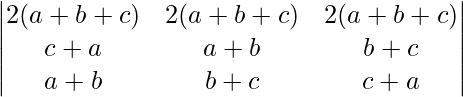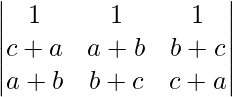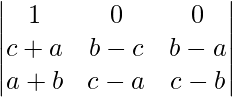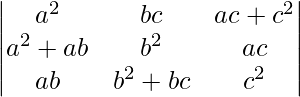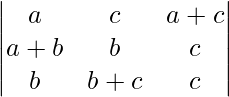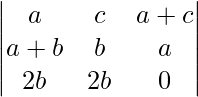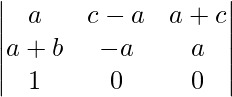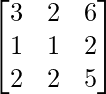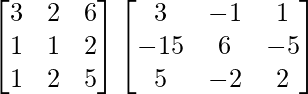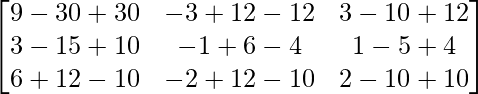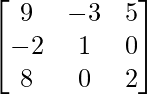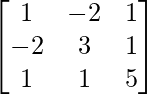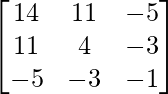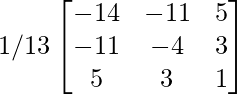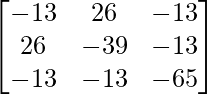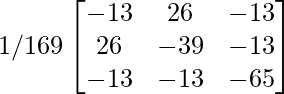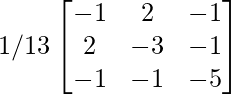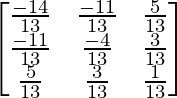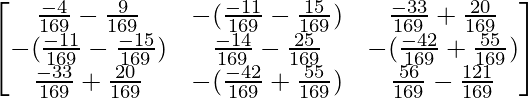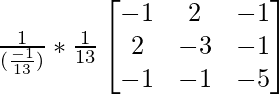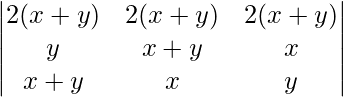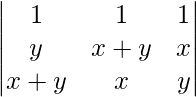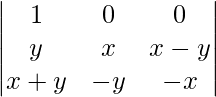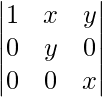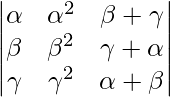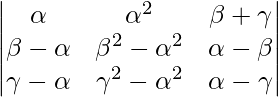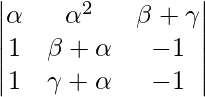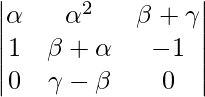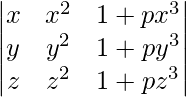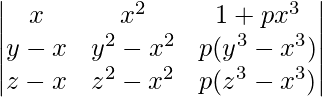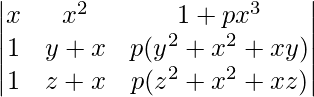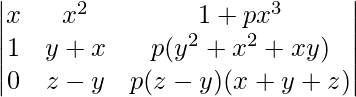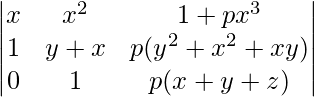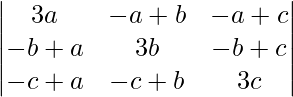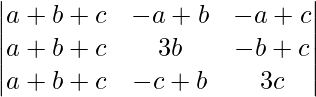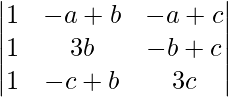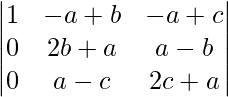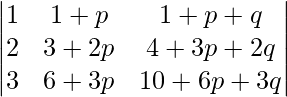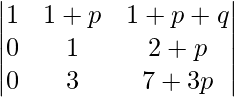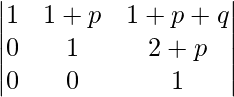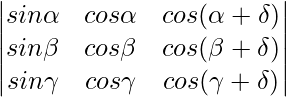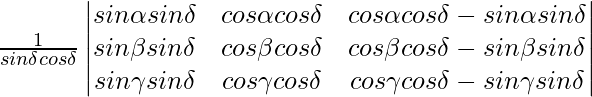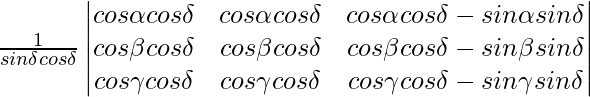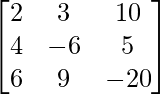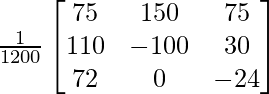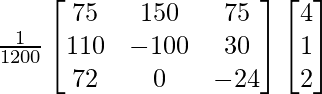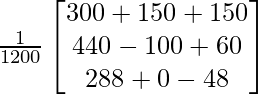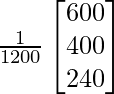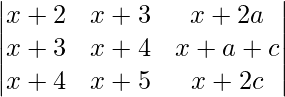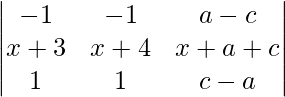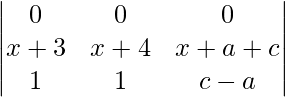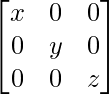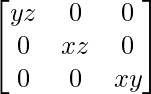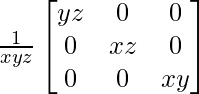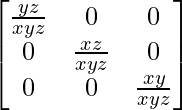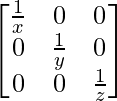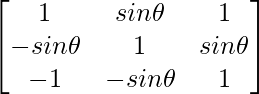Pregunta 1. Demuestra que el determinante 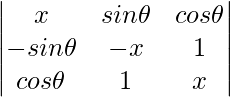 es independiente de θ.
es independiente de θ.
Solución:
un =
A = x(x 2 – 1) – sinθ(-x sinθ – cosθ) + cosθ(-sinθ + x cosθ)
A = x 3 – x + x sen2θ + senθcosθ – senθcosθ + x cos2θ
A = x 3 – x + x(sen2θ + cos2θ)
A = x 3 – x + x
A = x 3 (Independiente de θ).
Por lo tanto, es independiente de θ
Pregunta 2. Sin expandir el determinante, prueba que
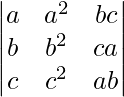 =
= 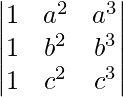
Solución:
IZQ =
=
=
(Quitando abc de C3)
=
=
(Aplicando transformación de columna entre C1 y C3 y entre C2 y C3)
= lado derecho
Por lo tanto, se prueba que
=
Pregunta 3. Evaluar 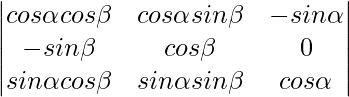
Solución:
un =
Expansión a lo largo de C3
A = -sen(-sen sen 2 β – cos 2 β sen) + cos(cos cos 2 β + cos sen 2 β)
A = sen 2 (sen 2 β + cos 2 β) + cos 2 (cos 2 β + sen 2 β)
A = sen 2 (1) + cos 2 (1)
un = 1
Pregunta 4. Si a, b y c son números reales, y Δ = 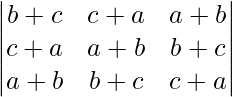 = 0
= 0
Demuestre que a + b + c = 0 o a = b = c
Solución:
Δ =
Aplicando R1 ⇢ R1 + R2 + R3
Δ =
= 2(a + b + c)
Aplicando C2 ⇢ C2-C1 y C3 ⇢ C3 – C1
Δ = 2(a + b + c)
Expansión a lo largo de R1
Δ = 2(a + b + c)(1)[(b – c)(c – b) – (b – a)(c – a)]
= 2(a + b + c)[-b 2 – c 2 + 2bc – bc + ba + ac – a 2 ]
= 2(a + b + c)[ab + bc + ca – a 2 – b 2 – c 2 ]
Según la pregunta Δ = 0
2(a + b + c)[ab + bc + ca – a 2 – b 2 – c 2 ] = 0
Desde arriba, puedes ver que a + b + c =0 o ab + bc + ca – a 2 – b 2 – c 2 = 0
Ahora,
ab + bc + ca – a 2 – b 2 – c 2 = 0
-2ab – 2bc – 2ac + 2a 2 + 2b 2 + 2c 2 = 0
(a – b) 2 + (b – c) 2 + (c – a) 2 = 0
(a – b) 2 = (b – c) 2 = (c – a) 2 = 0 (porque (a – b) 2 , (b – c) 2 , (c – a) 2 no son negativos)
(a – b) = (b – c) = (c – a) = 0
un = segundo = do
Por lo tanto, se prueba que si Δ = 0 entonces a + b + c = 0 o a = b = c.
Pregunta 5. Resuelve las ecuaciones 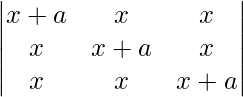 = 0, a ≠ 0
= 0, a ≠ 0
Solución:
= 0
Aplicando R1 ⇢ R1 + R2 + R3
= 0
(3x + a)
= 0
Aplicando C2 ⇢ C2-C1 y C3 ⇢ C3 – C1
(3x + a)
= 0
Expansión a lo largo de R1
(3x + a)[a 2 ] = 0
un 2 (3x + un) = 0
Pero un ≠ 0
Por lo tanto,
3x + a = 0
x = a/3
Pregunta 6. Demuestra que 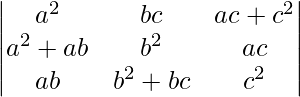 = 4a 2 b 2 c 2
= 4a 2 b 2 c 2
Solución:
un =
Sacando factores comunes a, b y c de C1, C2 y C3
A = abc
Aplicando R2 ⇢ R2 – R1 y R3 ⇢ R3 – R1
A = abc
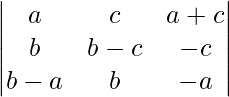
Aplicando R2 ⇢ R2 + R1
A = abc
A = 2ab 2c
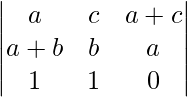
Aplicando C2 ⇢ C2 – C1
A = 2ab 2c
Expansión a lo largo de R3
A = 2ab 2 c[a(c – a) + a(a + c)]
= 2ab 2 c[ac – a 2 + a 2 + ac]
= 2ab 2 c(2ac)
= 4a 2 b 2 c 2
Por lo tanto, está probado.
Pregunta 7. Si A -1 = 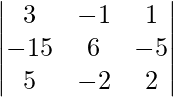 y B =
y B = 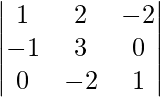 . Encontrar (AB) -1
. Encontrar (AB) -1
Solución:
|B| = 1(3 – 0) + 1(2 – 4) = 1
segundo 11 = 3 – 0 = 3
segundo 12 = 1
segundo 13 = 2 – 0 = 2
B 21 = -(2 – 4) = 2
segundo 22 = 1 – 0 = 1
segundo 23 = 2
segundo 31 = 0 + 6 = 6
B 32 = -(0 – 2) = 2
segundo 33 = 3 + 2 = 5
adj B =
B -1 = (adj B)/|B|
B – 1 =
Ahora,
(AB) -1 = B -1 A -1
(AB) -1 =
=
(AB) -1 =
Pregunta 8. Sea A = 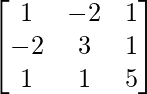 verificar que
verificar que
(i) [adj A] -1 = adj(A -1 )
(ii) (A -1 ) -1 = A
Solución:
un =
|A| = 1(15 – 1) + 2(-10 – 1) + 1(-2 – 3) = 14 – 27 = -13
UN 11 = 14
un 12 = 11
Un 13 = -5
21 = 11
22 = 4
Un 23 = -3
Un 31 = -5
A 32 = -3
A 33 = -1
adj A =
Arrr -1 = (ajustado A)/|A|
=
=
(i). |adj A| = 14(-4 – 9) – 11(-11 – 15) – 5(-33 + 20)
= 14(-13) – 11(-26) – 5(-13)
= -182 + 286 + 65 = 169
adj(adj A) =
[adj A] -1 = (adj(adj A))/|adj A|
=
=
Ahora, A – 1 =
=
adj(A -1 ) =
=
=
Por lo tanto, [adj A] -1 = adj(A -1 )
(ii). A – 1 =
adj A -1 =
|A -1 | = (1/13)3[-14 × (-13) +11 × (-26) + 5 × (-13)]
= (1/13)3 × (-169)
= -1/13
Ahora, (A -1 ) -1 = (adj A -1 )/|A -1 |
=
=
= un
Por lo tanto, se prueba que (A -1 ) -1 = A
Pregunta 9. Evaluar 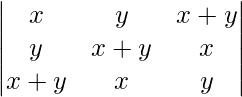
Solución:
un =
Aplicando R1 -> R1+R2+R3
un =
= 2(x+y)
Aplicando C2-> C2 – C1 y C3-> C3 – C1
A = 2(x + y)
Expansión a lo largo de R1
A = 2(x + y)[-x 2 + y(x – y)]
= -2(x + y)(x2 + y2 – yx)
A = -2(x 3 + y 3 )
Pregunta 10. Evaluar 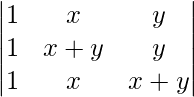
Solución:
un =
Aplicando R2->R2 – R1 y R3->R3 – R1
un =
Expansión a lo largo de C1
A = 1(xy – 0)
A = xy
Pregunta 11. Utilizando las propiedades de los determinantes, demuestre que:
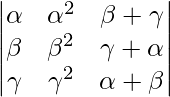 = (β – γ)(γ – )(– β)(+ β + γ)
= (β – γ)(γ – )(– β)(+ β + γ)
Solución:
un =
Aplicando R2->R2 – R1 y R3->R3 – R1
un =
A = (γ – )(β – )
Aplicando R3->R3 – R2
A = (γ – )(β – )
Expansión a lo largo de R3
A = (γ – )(β – )[-(γ – β)(-– β – γ)]
A = (γ – )(β – )(γ – β)(+ β + γ)
A = (β – γ)(γ – )(– β)(+ β + γ)
Por lo tanto, está probado.
Pregunta 12. Utilizando las propiedades de los determinantes, demuestre que:
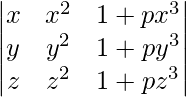 =(1 + pxyz)(x – y)(y – z)(z – x)
=(1 + pxyz)(x – y)(y – z)(z – x)
Solución:
un =
Aplicando R2->R2 – R1 y R3-> R3 – R1
un =
A = (y – x)(z – x)
Aplicando R3->R3 – R2
A = (y – x)(z – x)
A = (y – x)(z – x)(z – y)
Expansión a lo largo de R3
A = (x – y)(y – z)(z – x)[(-1)(p)(xy 2 + x 3 + x 2 y) + 1 + px 3 + p(x + y + z) (xy)]
= (x – y)(y – z)(z – x)[-pxy 2 – px 3 – px 2 y + 1 + px 3 + px 2 y + pxy 2 + pxyz]
= (x – y)(y – z)(z – x)(1 + pxyz)
Por lo tanto está probado.
Pregunta 13. Usando las propiedades de los determinantes, demuestre que
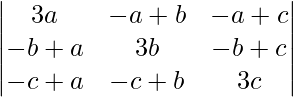 = 3(a + b + c)(ab + bc + ca)
= 3(a + b + c)(ab + bc + ca)
Solución:
un =
Aplicando C1->C1 + C2 + C3
un =
A = (a + b + c)
Aplicando R2->R2 – R1 y R3 ->R3 – R1
A = (a + b + c)
Expansión a lo largo de C1
A = (a + b + c)[(2b + a)(2c + a) – (a – b)(a – c)]
= (a + b + c)[4bc + 2ab + 2ac + a 2 – a 2 + ac + ba – bc]
=(a + b + c)(3ab + 3bc + 3ac)
A = 3(a + b + c)(ab + bc + ca)
Por lo tanto, está probado.
Pregunta 14. Usando las propiedades de los determinantes, demuestre que:
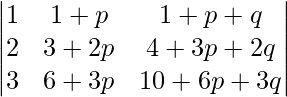 = 1
= 1
Solución:
un =
Aplicando R2->R2 – 2R1 y R3->R3 – 3R1
un =
Aplicando R3->R3 – 3R2
Expansión a lo largo de C1
A = 1 (1 – 0)
un = 1
Por lo tanto, está probado.
Pregunta 15. Usando las propiedades de los determinantes, demuestre que
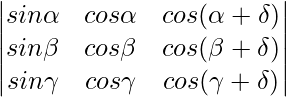 = 0
= 0
Solución:
un =
un =
Aplicando C1->C1 + C3
un =
desde arriba, puede ver que las dos columnas C1 y C2 son idénticas.
Por lo tanto A = 0
Por lo tanto, está probado.
Pregunta 16. Resuelve el sistema de las siguientes preguntas:
2/x + 3/y + 10/z = 4
4/x – 6/y + 5/z = 1
6/x + 9/y – 20/z = 2
Solución:
Suponga que 1/x = p; 1/y = q; 1/z = r
después. las ecuaciones anteriores serán como
2p + 3Q + 10r = 4
4p – 6q + 5r = 1
6p + 9q – 20r = 2
Esto se puede escribir en la forma AX=B
dónde,
un =
X =
B =
Tenemos,
|A| = 2(120 – 45) – 3(-80 – 30) + 10(36 + 36)
|A| = 150 + 330 + 720
|A| = 1200 ≠ 0
Por lo tanto, A es una array invertible.
UN 11 = 75
UN 12 = 110
13 = 72
21 = 150
A 22 = -100
Un 23 = 0
31 = 75
32 = 30
A 33 = -24
A -1 = (adj. A)/|A|
A – 1 =
Ahora,
X = A -1B
=
=
=
=
Desde arriba p = 1/2; q = 1/3 ; r = 1/5
Entonces, x = 2; y = 3; z = 5
Pregunta 17. Elija la respuesta correcta.
Si a, b, c están en AP entonces el determinante
(A) 0 (B) 1
(C) × (D) 2x
Solución:
un =
a, b y c están en AP Entonces, 2b = a + c
un =
Aplicando R1->R1 – R2 y R3->R3 – R2
un =
Aplicando R1->R1 + R3
un =
Todos los elementos de la primera fila son 0.
Por lo tanto A = 0
Entonces, la respuesta correcta es A.
Pregunta 18. Elija la respuesta correcta.
Si x, y, z son números reales distintos de cero, entonces el inverso de la array A = 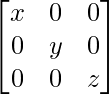 es
es
(A) 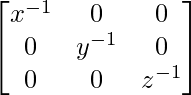
(B) xyz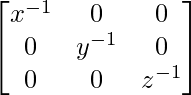
(C) 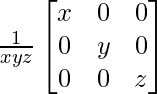
(D) 
Solución:
un =
|A| = x(yz – 0) = xyz ≠ 0
Por lo tanto, la array es invertible
Ahora,
A 11 = yz
un 12 = 0
un 13 = 0
21 = 0
A 22 = xz
Un 23 = 0
31 = 0
32 = 0
A 33 = xy
adj A =
A -1 = (adj. A)/|A|
A – 1 =
A – 1 =
A – 1 =
A – 1 =
Por lo tanto, la respuesta correcta es A.
Pregunta 19. Elija la respuesta correcta
Sea A = 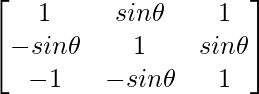 , donde 0 ≤ θ ≤ 2, entonces
, donde 0 ≤ θ ≤ 2, entonces
(A) Det(A) = 0 (B) Det(A) ∈ (2, ∞)
(C) Det(A) ∈ (2, 4) (D) Det(A) ∈ [2, 4]
Solución:
un =
|A| = 1(1 + sin2θ) – sinθ(-sinθ + sinθ) + 1(sin2θ + 1)
|A| = 1 + sen2θ + sen2θ + 1
= 2 + 2 sen2θ
= 2(1 + sen2θ)
Ahora 0 ≤ θ ≤ 2
Entonces, 0 ≤ senθ ≤ 1
0 ≤ sin2θ ≤ 1
0 + 1 ≤ 1 + sen2θ ≤ 1 + 1
2 ≤ 2(1 + sen2θ) ≤ 4
Det(A) ∈ [2, 4]
Por lo tanto, la respuesta correcta es D.