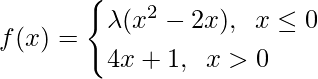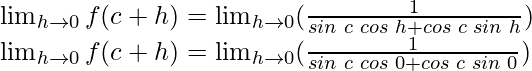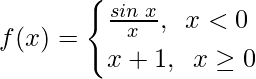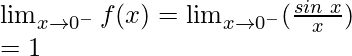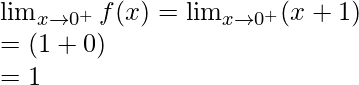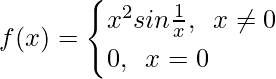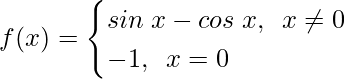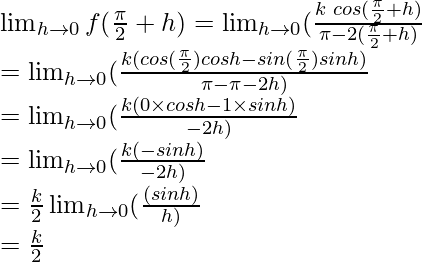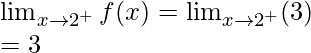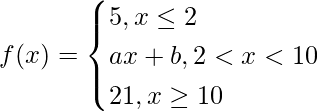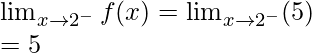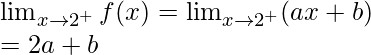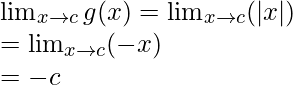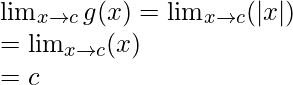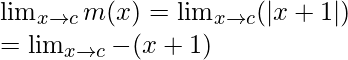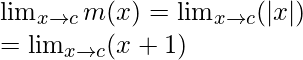Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 5 Continuidad y diferenciabilidad – Ejercicio 5.1

Pregunta 18. ¿Para qué valor de λ está definida la función por

$f(x)= \begin{cases} \lambda(x^2-2x), \hspace{0.2cm}x \leq0\\ 4x+1,\hspace{0.2cm}x>0 \end{cases}$

continua en x = 0? ¿Qué pasa con la continuidad en x = 1?

Solución:

Para ser una función continua, f(x) debe satisfacer lo siguiente en x = 0:

$\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0)$

Continuidad en x = 0,

Límite izquierdo = $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} \lambda(x^2-2x)$

= λ(0 ² – 2(0)) = 0

Límite derecho = $\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (4x+1)$

= λ4(0) + 1 = 1

Valor de la función en x = 0, f(0) = $\lambda(0^2-2(0)) = 0$

Como, 0 = 1 no puede ser posible

Por tanto, para ningún valor de λ, f(x) es continua.

Pero aquí, $\lim_{x \to 0^-} f(x) \neq \lim_{x \to 0^+} f(x)$

Continuidad en x = 1,

Límite izquierdo = $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (4x+1)$

= (4(1) + 1) = 5

Límite derecho = $\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (4x+1)$

= 4(1) + 1 = 5

Valor de función en x = 1, f(1) = 4(1) + 1 = 5

Como, $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) = 5$

Por tanto, la función es continua en x = 1 para cualquier valor de λ.

Pregunta 19. Demuestre que la función definida por g (x) = x – [x] es discontinua en todos los puntos integrales. Aquí [x] denota el mayor entero menor o igual que x.

Solución:

[x] es la función entera más grande que se define en todos los puntos integrales, por ejemplo

[2.5] = 2

[-1,96] = -2

x-[x] da la parte fraccionaria de x.

por ejemplo: 2,5 – 2 = 0,5

c ser un entero

Verifiquemos la continuidad en x = c,

Límite izquierdo = $\lim_{x \to c^-} f(x) = \lim_{x \to c^-} (x-[x])$

= (c – (c – 1)) = 1

Límite derecho = $\lim_{x \to c^+} f(x) = \lim_{x \to c^+} (x-[x])$

= (c – c) = 0

Valor de la función en x = c, f(c) = c – = c – c = 0

Como, $\lim_{x \to 1^-} f(x) \neq \lim_{x \to 1^+} f(x)$

Por lo tanto, la función es discontinua en la integral.

c no sea un entero

Verifiquemos la continuidad en x = c,

Límite izquierdo = $\lim_{x \to c^-} f(x) = \lim_{x \to c^-} (x-[x])$

= (c – (c – 1)) = 1

Límite derecho = $\lim_{x \to c^+} f(x) = \lim_{x \to c^+} (x-[x])$

= (c – (c – 1)) = 1

Valor de la función en x = c, f(c) = c – = c – (c – 1) = 1

Como, $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x)=f(1)=1$

Por lo tanto, la función es continua en la parte no integral.

Pregunta 20. ¿La función definida por f(x) = x ² – sen x + 5 es continua en x = π?

Solución:

Comprobemos la continuidad en x = π,

f(x) = x ² – sen x + 5

Sustituyamos, x = π+h

Cuando x⇢π, Continuidad en x = π

Límite izquierdo = $\lim_{x \to \pi^-} f(x) = \lim_{x \to \pi^-} (x^2 - sin \hspace{0.1cm}x + 5)$

= (π ² – senπ + 5) = π ² + 5

Límite derecho = $\lim_{x \to \pi^+} f(x) = \lim_{x \to \pi^+}(x^2 - sin \hspace{0.1cm}x + 5)$

= (π ² – senπ + 5) = π ² + 5

Valor de la función en x = π, f(π) = π ² – sen π + 5 = π ² + 5

Como, $\lim_{x \to \pi^-} f(x) = \lim_{x \to \pi^+} f(x) = f(\pi)$

Por lo tanto, la función es continua en x = π.

Pregunta 21. Discutir la continuidad de las siguientes funciones:

(a) f(x) = sen x + cos x

Solución:

Aquí,

f(x) = sen x + cos x

Tomemos, x = c + h

Cuando x⇢c entonces h⇢0

$\lim_{x \to c} f(x) = \lim_{h \to 0} f(c+h)$

Asi que,

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0}$ ( pecado ( c + h ) + cos ( c + h ))

Usando las identidades trigonométricas, obtenemos

sen(A + B) = sen A cos B + cos A sen B

cos(A + B) = cos A cos B – sen A sen B

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0}$ (( sinc cosh + cosc sinh ) + ( cosc cosh − sinc sinh ))

$\lim_{h \to 0} f(c+h)$ = (( sinc cos 0 + cosc sin 0) + ( cosc cos 0 − sinc sin 0))

cos 0 = 1 y sen 0 = 0

$\lim_{h \to 0} f(c+h)$ = ( sinc + cosc ) = f ( c )

Valor de la función en x = c, f(c) = sinc + cosc

Como, $\lim_{x \to c} f(x)$ = f(c) = sinc + cosc

Por lo tanto, la función es continua en x = c.

(b) f(x) = sen x – cos x

Solución:

Aquí,

f(x) = sen x – cos x

Tomemos, x = c+h

Cuando x⇢c entonces h⇢0

$\lim_{x \to c} f(x) = \lim_{h \to 0} f(c+h)$

Asi que,

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0}$ ( pecado ( c + h ) − cos ( c + h ))

Usando las identidades trigonométricas, obtenemos

sen(A + B) = sen A cos B + cos A sen B

cos(A + B) = cos A cos B – sen A sen B

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0}$ (( sinc cosh + cosc sinh ) − ( cosc cosh − sinc sinh ))

$\lim_{h \to 0} f(c+h)$ = (( sinc cos 0 + cosc sin 0) − ( cosc cos 0 − sinc sin 0))

cos 0 = 1 y sen 0 = 0

$\lim_{h \to 0} f(c+h)$ = ( sinc − cosc ) = f ( c )

Valor de la función en x = c, f(c) = sinc − cosc

Como, $\lim_{x \to c} f(x)$ = f(c) = sinc − cosc

Por lo tanto, la función es continua en x = c.

(c) f(x) = sen x . porque x

Solución:

Aquí,

f(x) = sen x + cos x

Tomemos, x = c+h

Cuando x⇢c entonces h⇢0

$\lim_{x \to c} f(x) = \lim_{h \to 0} f(c+h)$

Asi que,

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0}$ sen ( c + h ) × cos ( c + h ))

Usando las identidades trigonométricas, obtenemos

sen(A + B) = sen A cos B + cos A sen B

cos(A + B) = cos A cos B – sen A sen B

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0}$ (( sinc cosh + cosc sinh ) × ( cosc cosh − sinc sinh ))

$\lim_{h \to 0} f(c+h)$ = (( sinc cos 0 + cosc sin 0) × ( cosc cos 0 − sinc sin 0))

cos 0 = 1 y sen 0 = 0

$\lim_{h \to 0} f(c+h)$ = ( sinc × cosc ) = f ( c )

Valor de la función en x = c, f(c) = sinc × cosc

Como, $\lim_{x \to c} f(x)$ = f(c) = sinc × cosc

Por lo tanto, la función es continua en x = c.

Pregunta 22. Discuta la continuidad de las funciones coseno, cosecante, secante y cotangente.

Solución:

Continuidad del coseno

Aquí,

f(x) = cos x

Tomemos, x = c+h

Cuando x⇢c entonces h⇢0

$\lim_{x \to c} f(x) = \lim_{h \to 0} f(c+h)$

Asi que,

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (cos\hspace{0.1cm} (c+h))$

Usando las identidades trigonométricas, obtenemos

cos(A + B) = cos A cos B – sen A sen B

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0}$ (cosc cosh − sinc sinh )

$\lim_{h \to 0} f(c+h)$ = ( cosc cos 0 − sinc sin 0)

cos 0 = 1 y sen 0 = 0

$\lim_{h \to 0} f(c+h)$ = ( cosc ) = f ( c )

Valor de la función en x = c, f(c) = ( cosc )

Como, $\lim_{x \to c} f(x)$ = f(c) = ( cosc )

Por tanto, la función coseno es continua en x = c.

Continuidad de cosecante

Aquí,

f(x) = cosec x = $\frac{1}{sin \hspace{0.1cm}x}$

El dominio de cosec es R – {nπ}, n ∈ Entero

Tomemos, x = c + h

Cuando x⇢c entonces h⇢0

$\lim_{x \to c} f(x) = \lim_{h \to 0} f(c+h)$

Asi que,

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{sin \hspace{0.1cm}(c+h)})$

Usando las identidades trigonométricas, obtenemos

sen(A + B) = sen A cos B + cos A sen B

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{sin\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} h+cos\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} h})\\ \lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{sin\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} 0+cos\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} 0})$

cos 0 = 1 y sen 0 = 0

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{sin\hspace{0.1cm} c})$

Valor de la función en x = c, f(c) = $\frac{1}{sin\hspace{0.1cm} c}$

Como, $\lim_{x \to c} f(x) = f(c) = \frac{1}{sin\hspace{0.1cm} c}$

Por tanto, la función cosecante es continua en x = c.

Continuidad de la secante

Aquí,

f(x) = seg x = $\frac{1}{cos \hspace{0.1cm}x}$

Tomemos, x = c + h

Cuando x⇢c entonces h⇢0

$\lim_{x \to c} f(x) = \lim_{h \to 0} f(c+h)$

Asi que,

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{cos \hspace{0.1cm}(c+h)})$

Usando las identidades trigonométricas, obtenemos

cos(A + B) = cos A cos B – sen A sen B

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{cos\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} h-sin\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} h})$

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{cos\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} 0-sin\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} 0})$

cos 0 = 1 y sen 0 = 0

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{1}{cos\hspace{0.1cm} c})$

Valor de la función en x = c, f(c) = $\frac{1}{cos\hspace{0.1cm} c}$

Como, $\lim_{x \to c} f(x) = f(c) = \frac{1}{cos\hspace{0.1cm} c}$

Por tanto, la función secante es continua en x = c.

Continuidad de la cotangente

Aquí,

f(x) = cuna x = $\frac{cos \hspace{0.1cm}x}{sin \hspace{0.1cm}x}$

Tomemos, x = c+h

Cuando x⇢c entonces h⇢0

$\lim_{x \to c} f(x) = \lim_{h \to 0} f(c+h)$

Asi que,

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{cos \hspace{0.1cm}(c+h)}{sin \hspace{0.1cm}(c+h)})$

Usando las identidades trigonométricas, obtenemos

sen(A + B) = sen A cos B + cos A sen B

cos(A + B) = cos A cos B – sen A sen B

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{cos\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} h-sin\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} h}{sin\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} h+cos\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} h})$

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{cos\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} 0-sin\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} 0}{sin\hspace{0.1cm} c\hspace{0.1cm} cos\hspace{0.1cm} 0+cos\hspace{0.1cm} c\hspace{0.1cm} sin\hspace{0.1cm} 0})$

cos 0 = 1 y sen 0 = 0

$\lim_{h \to 0} f(c+h) = \lim_{h \to 0} (\frac{cos\hspace{0.1cm} c}{sin\hspace{0.1cm} c})$

$\lim_{h \to 0} f(c+h) = (\frac{cos\hspace{0.1cm} c}{sin\hspace{0.1cm} c})$

Valor de la función en x = c, f(c) = $\frac{cos\hspace{0.1cm} c}{sin\hspace{0.1cm} c}$

Como, $\lim_{x \to c} f(x) = f(c) = \frac{cos\hspace{0.1cm} c}{sin\hspace{0.1cm} c}$

Por tanto, la función cotangente es continua en x = c.

Pregunta 23. Encuentra todos los puntos de discontinuidad de f, donde

$f(x)= \begin{cases} \frac{sin \hspace{0.1cm}x}{x}, \hspace{0.2cm}x <0\\ x+1,\hspace{0.2cm}x\geq0 \end{cases}$

Solución:

Aquí,

De las dos funciones continuas g y h, obtenemos

$\frac{g(x)}{h(x)}$ = continua cuando h(x) ≠ 0

Para x < 0, f(x) = $\frac{sin \hspace{0.1cm}x}{x}$ , es continua

Por lo tanto, f(x) es continua x ∈ (-∞, 0)

Ahora, para x ≥ 0, f(x) = x + 1, que es un polinomio

Como los polinomios son continuos, entonces f(x) es continua x ∈ (0, ∞)

Entonces ahora, como f(x) es continua en x ∈ (-∞, 0) U (0, ∞)= R – {0}

Verifiquemos la continuidad en x = 0,

Límite izquierdo = $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (\frac{sin \hspace{0.1cm}x}{x})\\= 1$

Límite derecho = $\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (x+1)\\= (1+0)\\= 1$

Valor de función en x = 0, f(0) = 0 + 1 = 1

Como, $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) = 1$

Por lo tanto, la función es continua en x = 0.

Por lo tanto, la función es continua para cualquier número real.

Pregunta 24. Determinar si f definida por

$f(x)= \begin{cases} x^2sin\frac{1}{x}, \hspace{0.2cm}x \neq0\\ 0,\hspace{0.2cm}x=0 \end{cases}$

es una función continua?

Solución:

Aquí, como se da que

Para x = 0, f(x) = 0, que es una constante

Como constantes son continuas, por lo tanto f(x) es continua x ∈ = R – {0}

Verifiquemos la continuidad en x = 0,

Como sabemos, el rango de la función sin es [-1,1]. Entonces, -1 ≤ $sin(\frac{1}{x})$ ≤ 1 que es un número finito.

Límite = $\lim_{x \to 0} f(x) = \lim_{x \to 0} (x^2 sin(\frac{1}{x}))$

= (0 ² ×(número finito)) = 0

Valor de función en x = 0, f(0) = 0

Como, $\lim_{x \to 0} f(x) = f(0).$

Por lo tanto, la función es continua para cualquier número real.

Pregunta 25. Examina la continuidad de f, donde f está definida por

$f(x)= \begin{cases} sin\hspace{0.1cm}x-cos\hspace{0.1cm}x, \hspace{0.2cm}x\neq0\\ -1,\hspace{0.2cm}x=0 \end{cases}$

Solución:

Continuidad en x = 0,

Límite izquierdo = $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} (sin\hspace{0.1cm}x-cos\hspace{0.1cm}x)$

= ( sen 0 − cos 0) = 0 − 1 = −1

Límite derecho = $\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} (sin\hspace{0.1cm}x-cos\hspace{0.1cm}x)$

= ( sen 0 − cos 0) = 0 − 1 = −1

Valor de la función en x = 0, f(0) = sen 0 – cos 0 = 0 – 1 = -1

Como, $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0) = -1$

Por lo tanto, la función es continua en x = 0.

Continuidad en x = c (número real c≠0),

Límite izquierdo = $\lim_{x \to c^-} f(x) = \lim_{x \to c^-} (sin\hspace{0.1cm}x-cos\hspace{0.1cm}x)$

= ( sinc − cosc )

Límite derecho = $\lim_{x \to c^+} f(x) = \lim_{x \to c^+} (sin\hspace{0.1cm}x-cos\hspace{0.1cm}x)$

= ( sinc − cosc )

Valor de la función en x = c, f(c) = sen c – cos c

Como, $\lim_{x \to c^-} f(x) = \lim_{x \to c^+} f(x) = f(c) = (sin\hspace{0.1cm}c-cos\hspace{0.1cm}c)$

Entonces, concluyendo los resultados, obtenemos

La función f(x) es continua en cualquier número real.

Encuentre los valores de k para que la función f sea continua en el punto indicado en los ejercicios 26 a 29.

Pregunta 26. 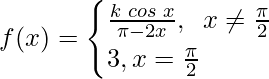$f(x)= \begin{cases} \frac{k\hspace{0.1cm}cos\hspace{0.1cm}x}{\pi-2x}, \hspace{0.2cm}x\neq\frac{\pi}{2}\\ 3,x=\frac{\pi}{2} \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = π/2.

Solución:

Continuidad en x = π/2

Tomemos x = $\frac{\pi}{2}+h$

Cuando x⇢π/2 entonces h⇢0

Sustituyendo x = $\frac{\pi}{2}$ +h, obtenemos

cos(A + B) = cos A cos B – sen A sen B

Límite = $\lim_{h \to 0} f(\frac{\pi}{2}+h) = \lim_{h \to 0} (\frac{k\hspace{0.1cm}cos(\frac{\pi}{2}+h)}{\pi-2(\frac{\pi}{2}+h)}\\= \lim_{h \to 0} (\frac{k(cos(\frac{\pi}{2})cos h-sin(\frac{\pi}{2})sinh)}{\pi-\pi-2h)}\\= \lim_{h \to 0} (\frac{k(0 \times cos h-1\times sinh)}{-2h)}\\= \lim_{h \to 0} (\frac{k(-sinh)}{-2h)}\\ = \frac{k}{2} \lim_{h \to 0} (\frac{(sinh)}{h)}\\ = \frac{k}{2}$

Valor de la función en x = $\frac{\pi}{2}, f(\frac{\pi}{2})$ = 3

Como, $\lim_{x \to \frac{\pi}{2}} f(x) = f(\frac{\pi}{2})$ debería satisfacer, para f(x) siendo continua

k/2 = 3

k = 6

Pregunta 27. 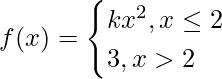$f(x)= \begin{cases} kx^2,x\leq2\\ 3,x>2 \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = 2

Solución:

Continuidad en x = 2

Límite izquierdo = $\lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} (kx^2)$

= k(2) ² = 4k

Límite derecho = $\lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} (3)\\= 3$

Valor de función en x = 2, f(2) = k(2) ² = 4k

Como, $\lim_{x \to 2^-} f(x) = \lim_{x \to 2^+} f(x)= f(2)$ debería satisfacer, para f(x) siendo continua

4k = 3

k = 3/4

Pregunta 28. 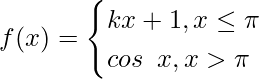$f(x)= \begin{cases} kx+1,x\leq\pi\\ cos \hspace{0.2cm}x,x>\pi \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = π

Solución:

Continuidad en x = π

Límite izquierdo = $\lim_{x \to \pi^-} f(x) = \lim_{x \to \pi^-} (kx+1)$

= k(π) + 1

Límite derecho = $\lim_{x \to \pi^+} f(x) = \lim_{x \to \pi^+} (cos x)$

= cos(π) = -1

Valor de la función en x = π, f(π) = k(π) + 1

Como, $\lim_{x \to \pi^-}f(x) = \lim_{x \to \pi^+} f(x)= f(\pi)$ debería satisfacer, para f(x) siendo continua

kπ + 1 = -1

k = -2/π

Pregunta 29. 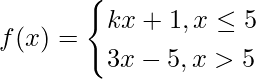$f(x)= \begin{cases} kx+1,x\leq5\\ 3x-5,x>5 \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = 5

Solución:

Continuidad en x = 5

Límite izquierdo = $\lim_{x \to 5^-} f(x) = \lim_{x \to 5^-} (kx+1)$

= k(5) + 1 = 5k + 1

Límite derecho = $\lim_{x \to 5^+} f(x) = \lim_{x \to 5^+} (3x-5)$

= 3(5) – 5 = 10

Valor de la función en x = 5, f(5) = k(5) + 1 = 5k + 1

Como, $\lim_{x \to 5^-} f(x) = \lim_{x \to 5^+} f(x)= f(5)$ debería satisfacer, para f(x) siendo continua

5k + 1 = 10

k = 9/5

Pregunta 30. Encuentra los valores de a y b tales que la función definida por

$f(x)= \begin{cases} 5,x\leq2\\ ax+b,2<x<10\\ 21,x\geq10 \end{cases}$

es una función continua

Solución:

Continuidad en x = 2

Límite izquierdo = $\lim_{x \to 2^-} f(x) = \lim_{x \to 2^-} (5)\\= 5$

Límite derecho = $\lim_{x \to 2^+} f(x) = \lim_{x \to 2^+} (ax+b)\\= 2a+b$

Valor de la función en x = 2, f(2) = 5

Como, $\lim_{x \to 2^-} f(x) = \lim_{x \to 2^+} f(x)= f(2)$ debería satisfacer, para f(x) siendo continua en x = 2

2a + b = 5 ……………………(1)

Continuidad en x = 10

Límite izquierdo = $\lim_{x \to 10^-} f(x) = \lim_{x \to 10^-} (ax+b)$

= 10a + b

Límite derecho = $\lim_{x \to 10^+} f(x) = \lim_{x \to 10^+} (21)$

= 21

Valor de la función en x = 10, f(10) = 21

Como, $\lim_{x \to 10^-} f(x) = \lim_{x \to 10^+} f(x)= f(10)$ debería satisfacer, para f(x) siendo continua en x = 10

10a + b = 21 ……………………(2)

Resolviendo la ecuación (1) y la ecuación (2), obtenemos

un = 2

segundo = 1

Pregunta 31. Demostrar que la función definida por f(x) = cos (x ² ) es una función continua

Solución:

Echemos

g(x) = cos x

h(x) = ^x2

g(h(x)) = cos (x ² )

Para demostrar que g(h(x)) es continua, g(x) y h(x) deben ser continuas.

Continuidad de g(x) = cos x

Verifiquemos la continuidad en x = c

x = c + h

g(c + h) = porque (c + h)

Cuando x⇢c entonces h⇢0

cos(A + B) = cos A cos B – sen A sen B

Límite = $\lim_{h \to 0} g(c+h) = \lim_{h \to 0} (cos(c+h))\\ = \lim_{h \to 0}$ ( cosc cosh − sinc sinh )

= cosc cos 0 − sinc sen 0 = cosc

Valor de la función en x = c, g(c) = cos c

Como, $\lim_{x \to c} g(x) = g(c) = cos\hspace{0.1cm} c$

La función g(x) es continua en cualquier número real.

Continuidad de h(x) = x ²

Verifiquemos la continuidad en x = c

Límite = $\lim_{x \to c} h(x) = \lim_{x \to c} (x^2)$

= do ²

Valor de la función en x = c, h(c) = c ²

Como, $\lim_{x \to c} h(x) = h(c) = c^2$

La función h(x) es continua en cualquier número real.

Como g(x) y h(x) son continuas, entonces g(h(x)) = cos(x ² ) también es continua.

Pregunta 32. Demuestra que la función definida por f(x) = | porque x | es una función continua.

Solución:

Echemos

g(x) = |x|

m(x) = cos x

g(m(x)) = |cos x|

Para demostrar que g(m(x)) es continua, g(x) y m(x) deben ser continuas.

Continuidad de g(x) = |x|

Como sabemos, la función de módulo funciona de manera diferente.

En |x – 0|, |x| = x cuando x ≥ 0 y |x| = -x cuando x < 0

Verifiquemos la continuidad en x = c

Cuando c < 0

Límite = $\lim_{x \to c} g(x) = \lim_{x \to c} (|x|)\\= \lim_{x \to c} (-x)\\ = -c$

Valor de la función en x = c, g(c) = |c| = -c

Como, $\lim_{x \to c} g(x) = g(c) = -c$

Cuando c ≥ 0

Límite = $\lim_{x \to c} g(x) = \lim_{x \to c} (|x|)\\= \lim_{x \to c} (x)\\ = c$

Valor de la función en x = c, g(c) = |c| = do

Como, $\lim_{x \to c} g(x) = g(c) = c$

La función g(x) es continua en cualquier número real.

Continuidad de m(x) = cos x

Verifiquemos la continuidad en x = c

x = c + h

m(c + h) = porque (c + h)

Cuando x⇢c entonces h⇢0

cos(A + B) = cos A cos B – sen A sen B

Límite = $\lim_{h \to 0} m(c+h) = \lim_{h \to 0} (cos(c+h))\\ = \lim_{h \to 0}$ ( cosc cosh − sinc sinh )

= cosc cos 0 − sinc sen 0 = cosc

Valor de la función en x = c, m(c) = cos c

Como, $\lim_{x \to c} m(x) = m(c) = cos \hspace{0.1cm}c$

La función m(x) es continua en cualquier número real.

Como g(x) y m(x) son continuas, entonces g(m(x)) = |cos x| también es continuo.

Pregunta 33. Examina ese pecado | x | es una función continua.

Solución:

Echemos

g(x) = |x|

m(x) = sen x

m(g(x)) = sen |x|

Para demostrar que m(g(x)) es continua, g(x) y m(x) deben ser continuas.

Continuidad de g(x) = |x|

Como sabemos, la función de módulo funciona de manera diferente.

En |x-0|, |x|=x cuando x≥0 y |x|=-x cuando x<0

Verifiquemos la continuidad en x = c

Cuando c < 0

Límite = $\lim_{x \to c} g(x) = \lim_{x \to c} (|x|)\\= \lim_{x \to c} (-x)\\ = -c$

Valor de la función en x = c, g(c) = |c| = -c

Como, $\lim_{x \to c} g(x) = g(c) = -c$

Cuando c ≥ 0

Límite = $\lim_{x \to c} g(x) = \lim_{x \to c} (|x|)\\= \lim_{x \to c} (x)\\ = c$

Valor de la función en x = c, g(c) = |c| = do

Como, $\lim_{x \to c} g(x) = g(c) = c$

La función g(x) es continua en cualquier número real.

Continuidad de m(x) = sen x

Verifiquemos la continuidad en x = c

x = c + h

m(c + h) = sen (c + h)

Cuando x⇢c entonces h⇢0

sen(A + B) = sen A cos B + cos A sen B

Límite = $\lim_{h \to 0} m(c+h) = \lim_{h \to 0} (sin(c+h))\\ = \lim_{h \to 0}$ ( sinc cosh + cosc sinh )

= sinc cos 0 + cos csen 0 = sinc

Valor de la función en x = c, m(c) = sen c

Como, $\lim_{x \to c} m(x) = m(c) = sin c$

La función m(x) es continua en cualquier número real.

Como g(x) y m(x) son continuas, entonces m(g(x)) = sen |x| también es continuo.

Pregunta 34. Encuentra todos los puntos de discontinuidad de f definidos por f(x) = | x | – | x + 1 |

Solución:

Echemos

g(x) = |x|

m(x) = |x + 1|

g(x) – m(x) = | x | – | x + 1 |

Para demostrar que g(x) – m(x) es continua, g(x) y m(x) deben ser continuas.

Continuidad de g(x) = |x|

Como sabemos, la función de módulo funciona de manera diferente.

En |x – 0|, |x| = x cuando x≥0 y |x| = -x cuando x < 0

Verifiquemos la continuidad en x = c

Cuando c < 0

Límite = $\lim_{x \to c} g(x) = \lim_{x \to c} (|x|)\\= \lim_{x \to c} (-x)\\ = -c$

Valor de la función en x = c, g(c) = |c| = -c

Como, $\lim_{x \to c} g(x) = g(c) = -c$

Cuando c ≥ 0

Límite = $\lim_{x \to c} g(x) = \lim_{x \to c} (|x|)\\= \lim_{x \to c} (x)\\ = c$

Valor de la función en x = c, g(c) = |c| = do

Como, $\lim_{x \to c} g(x) = g(c) = c$

La función g(x) es continua en cualquier número real.

Continuidad de m(x) = |x + 1|

Como sabemos, la función de módulo funciona de manera diferente.

En |x + 1|, |x + 1| = x + 1 cuando x ≥ -1 y |x + 1| = -(x + 1) cuando x < -1

Verifiquemos la continuidad en x = c

Cuando c < -1

Límite = $\lim_{x \to c} m(x) = \lim_{x \to c} (|x+1|)\\= \lim_{x \to c} -(x+1)$

= -(c + 1)

Valor de la función en x = c, m(c) = |c + 1| = -(c + 1)

Como, $\lim_{x \to c} m(x) = m(c) = -(c+1)$

Cuando c ≥ -1

Límite = $\lim_{x \to c} m(x) = \lim_{x \to c} (|x|)\\= \lim_{x \to c} (x+1)$

= c + 1

Valor de la función en x = c, m(c) = |c| = c + 1

Como, $\lim_{x \to c} m(x)$ = m(c) = c + 1

La función m(x) es continua en cualquier número real.

Como g(x) y m(x) son continuas, entonces g(x) – m(x) = |x| – |x + 1| también es continuo.

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 5 Continuidad y diferenciabilidad – Ejercicio 5.1 | conjunto 2

Pregunta 18. ¿Para qué valor de λ está definida la función por

$f(x)= \begin{cases} \lambda(x^2-2x), \hspace{0.2cm}x \leq0\\ 4x+1,\hspace{0.2cm}x>0 \end{cases}$

continua en x = 0? ¿Qué pasa con la continuidad en x = 1?

Pregunta 19. Demuestre que la función definida por g (x) = x – [x] es discontinua en todos los puntos integrales. Aquí [x] denota el mayor entero menor o igual que x.

Pregunta 20. ¿La función definida por f(x) = x ² – sen x + 5 es continua en x = π?

Pregunta 21. Discutir la continuidad de las siguientes funciones:

(a) f(x) = sen x + cos x

(b) f(x) = sen x – cos x

(c) f(x) = sen x . porque x

Pregunta 22. Discuta la continuidad de las funciones coseno, cosecante, secante y cotangente.

Pregunta 23. Encuentra todos los puntos de discontinuidad de f, donde

$f(x)= \begin{cases} \frac{sin \hspace{0.1cm}x}{x}, \hspace{0.2cm}x <0\\ x+1,\hspace{0.2cm}x\geq0 \end{cases}$

Pregunta 24. Determinar si f definida por

$f(x)= \begin{cases} x^2sin\frac{1}{x}, \hspace{0.2cm}x \neq0\\ 0,\hspace{0.2cm}x=0 \end{cases}$

es una función continua?

Pregunta 25. Examina la continuidad de f, donde f está definida por

$f(x)= \begin{cases} sin\hspace{0.1cm}x-cos\hspace{0.1cm}x, \hspace{0.2cm}x\neq0\\ -1,\hspace{0.2cm}x=0 \end{cases}$

Encuentre los valores de k para que la función f sea continua en el punto indicado en los ejercicios 26 a 29.

Pregunta 26. $f(x)= \begin{cases} \frac{k\hspace{0.1cm}cos\hspace{0.1cm}x}{\pi-2x}, \hspace{0.2cm}x\neq\frac{\pi}{2}\\ 3,x=\frac{\pi}{2} \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = π/2.

Pregunta 27. $f(x)= \begin{cases} kx^2,x\leq2\\ 3,x>2 \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = 2

Pregunta 28. $f(x)= \begin{cases} kx+1,x\leq\pi\\ cos \hspace{0.2cm}x,x>\pi \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = π

Pregunta 29. $f(x)= \begin{cases} kx+1,x\leq5\\ 3x-5,x>5 \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = 5

Pregunta 30. Encuentra los valores de a y b tales que la función definida por

$f(x)= \begin{cases} 5,x\leq2\\ ax+b,2<x<10\\ 21,x\geq10 \end{cases}$

es una función continua

Pregunta 31. Demostrar que la función definida por f(x) = cos (x ² ) es una función continua

Pregunta 32. Demuestra que la función definida por f(x) = | porque x | es una función continua.

Pregunta 33. Examina ese pecado | x | es una función continua.

Pregunta 34. Encuentra todos los puntos de discontinuidad de f definidos por f(x) = | x | – | x + 1 |

Deja una respuesta Cancelar la respuesta

Pregunta 18. ¿Para qué valor de λ está definida la función por

continua en x = 0? ¿Qué pasa con la continuidad en x = 1?

Pregunta 19. Demuestre que la función definida por g (x) = x – [x] es discontinua en todos los puntos integrales. Aquí [x] denota el mayor entero menor o igual que x.

Pregunta 20. ¿La función definida por f(x) = x 2 – sen x + 5 es continua en x = π?

Pregunta 21. Discutir la continuidad de las siguientes funciones:

(a) f(x) = sen x + cos x

(b) f(x) = sen x – cos x

(c) f(x) = sen x . porque x

Pregunta 22. Discuta la continuidad de las funciones coseno, cosecante, secante y cotangente.

Pregunta 23. Encuentra todos los puntos de discontinuidad de f, donde

Pregunta 24. Determinar si f definida por

es una función continua?

Pregunta 25. Examina la continuidad de f, donde f está definida por

Encuentre los valores de k para que la función f sea continua en el punto indicado en los ejercicios 26 a 29.

Pregunta 26. en x = π/2.

Pregunta 27. en x = 2

Pregunta 28. en x = π

Pregunta 29. en x = 5

Pregunta 30. Encuentra los valores de a y b tales que la función definida por

es una función continua

Pregunta 31. Demostrar que la función definida por f(x) = cos (x 2 ) es una función continua

Pregunta 32. Demuestra que la función definida por f(x) = | porque x | es una función continua.

Pregunta 33. Examina ese pecado | x | es una función continua.

Pregunta 34. Encuentra todos los puntos de discontinuidad de f definidos por f(x) = | x | – | x + 1 |

Deja una respuesta Cancelar la respuesta

Pregunta 20. ¿La función definida por f(x) = x ² – sen x + 5 es continua en x = π?

Pregunta 26. $f(x)= \begin{cases} \frac{k\hspace{0.1cm}cos\hspace{0.1cm}x}{\pi-2x}, \hspace{0.2cm}x\neq\frac{\pi}{2}\\ 3,x=\frac{\pi}{2} \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = π/2.

Pregunta 27. $f(x)= \begin{cases} kx^2,x\leq2\\ 3,x>2 \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = 2

Pregunta 28. $f(x)= \begin{cases} kx+1,x\leq\pi\\ cos \hspace{0.2cm}x,x>\pi \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = π

Pregunta 29. $f(x)= \begin{cases} kx+1,x\leq5\\ 3x-5,x>5 \end{cases} \hspace{0.1cm}\hspace{0.1cm}$ en x = 5

Pregunta 31. Demostrar que la función definida por f(x) = cos (x ² ) es una función continua