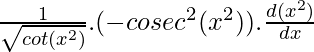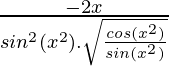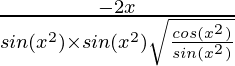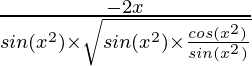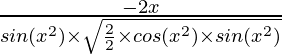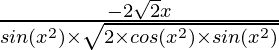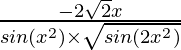Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 5 Continuidad y diferenciabilidad – Ejercicio 5.2

Diferenciar la función con respecto a x en las Preguntas 1 a 8

Pregunta 1. Sin(x ² + 5)

Solución:

y = sen(x ² + 5)

$\frac{dy}{dx}$ = $\frac{d(sin(x^2+5)}{dx}$

= cos(x ² + 5) × $\frac{d(x^2+5)}{dx}$

= cos(x ² + 5) × (2x)

dy/dx = 2xcos(x ² + 5)

Pregunta 2. cos(sen x)

Solución:

y = cos(sen x)

$\frac{dy}{dx}$ = $\frac{d\cos(sen x)}{dx}$

= -sen(sen x) × $\frac{d\senx}{dx}$

= -sen(sen x)cos x

Pregunta 3. sen(ax + b)

Solución:

y = sen(ax + b)

$\frac{dy}{dx}=\frac{d}{dx}sin(ax+b)$

$=cos(ax+b)\frac{d}{dy}(ax+b)$

= a cos(ax + b)

Pregunta 4. Sec(tan(√x)

Solución:

y = seg(tan√x)

$\frac{dy}{dx}$ = $\frac{d \ (sec(tan√x)) }{dx}$

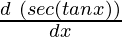
= seg(tan √x) × tan(√x) × $\frac{d \ (tan√x) }{dx}$

= seg (tan √x) × tan (tan √x) × sec2√x × $\frac{d \ (√x)}{dx}$

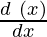
= sec(tan√x)tan(tan√x)(sec2√x)1/(2√x)

= 1/(2√x) × seg(tan√x)tan(tan√x)(sec2√x)

Pregunta 5. 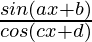$\frac{sin(ax+b)}{cos(cx+d)}$

Solución:

y = $\frac{sin(ax+b)}{cos(cx+d)}$

$\frac{dy}{dx} = \frac{d (\frac{sin(ax+b)}{cos(cx+d)})}{dx}$

$=\frac{cos(cx+d)\frac{d}{dx}sin(ax+b)-sin(ax+b)\frac{d}{dx}cos(cx+d)}{(cos(cx+d))}$

= $\frac{cos(cx+d)cos(ax+b)(a)+sin(ax+b)sin(cx+d)(c)}{cos^2(cx+b)}$

Pregunta 6. cos x ³ .sen ² (x ⁵ )

Solución:

y = cos x ³ .sen ² (x ⁵ )

$\frac{dy}{dx} = cosx^3\frac{d(sin^2(x^5)}{dx}+sin^2(x^5)\frac{d(cosx^3)}{dx}$

= $cosx^3.2sin(x^5)\frac{d(sin(x^5)}{dx}+sin^2(x^5)(-sinx^3)\frac{d(x^3)}{dx}$

= cos x ³ .2sen(x ⁵ ) .cos(x ⁵ (5x ⁴ )(5x ⁴ ) – sen ² (x ⁵ ).sen x ³ .3x ²

= 10x ⁴ cos x ³ sen(x ⁵ )cos(x ⁵ ) – 3x ² sen ² (x ⁵ )sen x ³

Pregunta 7. 2√(cos(x ² ))

Solución:

y = 2√(cos(x ² ))

$\frac{dy}{dx}$ = $\frac{\ d(2\sqrt{cos(x2})}{dx}$

= 2 $\frac{\ d(\sqrt{cos(x^2})}{dx}$

= $2\frac{1}{2\sqrt {cotx^2}}.\frac{d(cotx^2)}{dx}$

= $\frac{1}{\sqrt {cot(x^2)}}.(-cosec^2(x^2)).\frac{d(x^2)}{dx}$

= $\frac{1}{\sqrt {cot(x^2)}}.(-cosec^2(x^2)).2x$

= $\frac{-2xcosec^2x^2}{\sqrt{cot(x^2)}}$

= $\frac{-2x}{sin^2(x^2).\sqrt{\frac{cos(x^2)}{sin(x^2)}}}$

= $\frac{-2x}{sin(x^2) \times sin(x^2)\sqrt{\frac{cos(x^2)}{sin(x^2)}}}$

= $\frac{-2x}{sin(x^2) \times \sqrt{sin(x^2) \times \frac{cos(x^2)}{sin(x^2)}}}$

= $\frac{-2x}{sin(x^2) \times \sqrt{cos(x^2) \times {sin(x^2)}}}$

= $\frac{-2x}{sin(x^2) \times \sqrt{\frac{2}{2} \times cos(x^2) \times {sin(x^2)}}}$

= $\frac{-2\sqrt{2}x}{sin(x^2) \times \sqrt{2 \times cos(x^2) \times {sin(x^2)}}}$

= $\frac{-2\sqrt{2}x}{sin(x^2) \times \sqrt{sin(2x^2)}}$

Pregunta 8. coseno (√x)

Solución:

y = coseno (√x)

dy/dx = -sen√x $\frac{d\sqrt{x}}{dx}$

= $-sin\sqrt{x}\frac{1}{2}(x)^\frac{-1}{2}$

= $\frac{-sin\sqrt{x}}{2\sqrt{x}}$

Pregunta 9. Demostrar que la función f dada por f(x) = |x – 1|, x ∈ R no es diferenciable en x = 1.

Solución:

$RHD=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h}$

= $\lim_{h\to 0}\frac{f(1+h)-f(1)}{h}$

$= \lim_{h\to 0}\frac{((1+h)-1)-(1-1)}{h}$

= $\lim_{h\to 0}\frac{h-0}{h}$

= $\lim_{h\to 0}(1)$

= +1

$LHD=\lim_{h\to 0}\frac{f(x)-f(x-h)}{h}$

= $\lim_{h\to 0}\frac{(1)-f(1-h)}{h}$

$\lim_{h\to 0}\frac{(1-1)-(-(1-h)-1)}{h}$

= $\lim_{h\to 0}\frac{0-h}{h}$

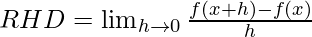
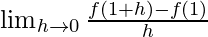
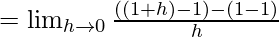
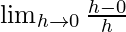
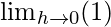
= $\lim_{h\to 0}(-1)$

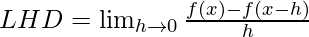
= -1

LHD ≠ RHD

Por lo tanto, f(x) no es diferenciable en x = 1

Pregunta 10. Demostrar que la función entera mayor definida por f(x) = [x], 0 < x < 3 no es diferenciable en x = 1 y x = 2.

Solución:

Dado: f(x) = [x], 0 < x < 3

LHS:

f'(1) = $\lim_{h\to0} \frac{f(x - h)-f(x)}{-h}$

= $\lim_{h\to0} \frac{f(1 - h)-1}{-h}$

= $\lim_{h\to0} \frac{0-1}{-h}$

= ∞

lado derecho:

f'(1) = $\lim_{h\to0} \frac{f(x + h) - f(x)}{h}$

= $\lim_{h\to0} \frac{f(1 + h) - f(1)}{h}$

= $\lim_{h\to0} \frac{1-1}{h}$

= $\lim_{h\to0} \frac{0}{h}$

= 0

IZQ ≠ DERECHO

Entonces, la f(x) = [x] dada no es diferenciable en x = 1.

De manera similar, la f(x) = [x] dada no es diferenciable en x = 2.