Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 5 Continuidad y diferenciabilidad – Ejercicio 5.3

Encuentre 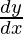$\frac{dy}{dx}$ lo siguiente:

Pregunta 1. 2x + 3y = sen x

Solución:

Al diferenciar ambos lados de x, obtenemos

2 + 3 $\frac{dy}{dx}$ = cos x

3 $\frac{dy}{dx}$ = cos x – 2

$\frac{dy}{dx}$ = (cosx – 2)/3

Pregunta 2. 2x + 3y = sen y

Solución:

Al diferenciar ambos lados de x, obtenemos

2 + 3 $\frac{dy}{dx}$ = cos y $\frac{dy}{dx}$

(acogedor – 3) $\frac{dy}{dx}$ = 2

$\frac{dy}{dx} = \frac{2}{(cos⁡y - 3)}$

Pregunta 3. ax + by ² = cos y

Solución:

Al diferenciar ambos lados de x, obtenemos

a + b * 2y( $\frac{dy}{dx}$ ) = -sen y * $\frac{dy}{dx}$

(2by + seno) $\frac{dy}{dx}$ = -a

$\frac{dy}{dx} = \frac{-a}{2by+siny}$

Pregunta 4. xy + y ² = tan x + y

Solución:

Al diferenciar ambos lados de x, obtenemos

(x * $\frac{dy}{dx}$ + y) + 2y $\frac{dy}{dx}$ = segundo ² x + $\frac{dy}{dx}$

(x + 2y – 1) $\frac{dy}{dx}$ = segundo ² x – y

$\frac{dy}{dx} = \frac{(sec^2x-y)}{(x+2y-1)}$

Pregunta 5. x ² + xy + y ² = 100

Solución:

Al diferenciar ambos lados de x, obtenemos

2x + (x $\frac{dy}{dx}$ + y) + 2y $\frac{dy}{dx}$ = 0

(x + 2y) * $\frac{dy}{dx}$ = -(2x + y)

$\frac{dy}{dx} = \frac{-(2x + y)}{(x + 2y)}$

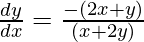
Pregunta 6. x ³ + x ² y + xy ² + y ³ = 81

Solución:

Diferenciar ambos lados wrt x

3x ² +(x ² $\frac{dy}{dx}$ + y * 2x) + (x * 2y * $\frac{dy}{dx}$ + y ² ) + 3y ² * $\frac{dy}{dx}$ = 0

(x2 ⁺ 2xy + 3y2 ⁾ = $\frac{dy}{dx}$ -(3×2 ⁺ 2xy + ^y2 )

$\frac{dy}{dx} = \frac{3x^2 + 2xy + y^2}{x^2 + 2xy + 3y^2}$

Pregunta 7. Sen ² y + cos xy = π

Solución:

Diferenciar ambos lados wrt x

2 sen y * $\frac{dy}{dx}$ (sen⁡y) – sen(xy) * $\frac{dy}{dx}$ xy = 0

2sen y * cómodo $\frac{dy}{dx}$ – sin(xy)(x * $\frac{dy}{dx}$ + y) = 0

(2sen cos y – sen (xy) – x)) $\frac{dy}{dx}$ = y(xy)

$\frac{dy}{dx} = \frac{y sin⁡(xy)}{2 sin⁡ y cos⁡ y - x sin⁡ (xy)}$

$\frac{dy}{dx} = \frac{ysin(xy)}{sin2y - x sinxy}$

Pregunta 8. sen ² x + cos ² y = 1

Solución:

2 sen x * $\frac{dy}{dx}$ (sen ⁡x) + 2 cos y * $\frac{dy}{dx}$ (cos ⁡y) = 0

2 sen x * cos x + 2 cos y*(-sen y) * $\frac{dy}{dx}$ = 0

2 sen x * cos x – 2 cos x – 2 cos y sen y * $\frac{dy}{dx}$ = 0

Sin(2x) – sin(2y) – $\frac{dy}{dx}$ = 0

$\frac{dy}{dx} = \frac{sin(2x)}{sin(2y)}$

Pregunta 9. y = sen ^-1 (\frac{2x}{(1 + x ² )}

Solución:

Poner x = tanθ

θ = bronceado ^-1 x

$y = sin^{-1}\frac{2tanθ}{1+tan^2θ}$

y = sen ^-1 (sen 2θ)

y = 2θ

y = 2 tan ^-1 x -(1)

Al diferenciar la ecuación (1), obtenemos

$\frac{dy}{dx} = \frac{2}{(1 + x^2)}$

Pregunta 10. 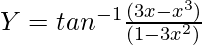$Y=tan^{-1}\frac{(3x-x^3)}{(1-3x^2 )}$ , -1/√3 < x < 1/√3

Solución:

Poner x = tanθ

θ = bronceado ^-1 x

y = $tan^{-1}(\frac{3tanθ - tan^3θ}{1-3tan^2θ})$

y = tan ^-1 (tan 3θ)

y = 3θ

y = 3tan ^-1 x -(1)

Al diferenciar la ecuación (1), obtenemos

$\frac{dy}{dx} = \frac{3}{(1 + x^2)}$

Pregunta 11. 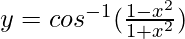$y = cos^{-1}(\frac{1-x^2}{1+x^2})$ , 0 < x < 1

Solución:

Poner x = tanθ

θ = bronceado ^-1 x

y = $cos^{-1}(\frac{1-tan^2θ}{1+tan^2θ})$

y = cos ^-1 (cos 2θ)

y = 2θ

y = 2 tan ^-1 x -(1)

Al diferenciar la ecuación (1), obtenemos

$\frac{dy}{dx} = \frac{2}{(1 + x^2)}$

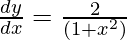
Pregunta 12. 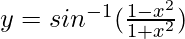$y = sin^{-1}(\frac{1-x^2}{1+x^2})$ , 0 < x < 1

Solución:

Poner x = tanθ

θ = bronceado ^-1 x

$y = sin^{-1}(\frac{1 - tan^2θ}{1 + tan^2θ})$

y = sen ^-1 (cos 2θ)

y = sen ^-1 (sen (π/2 – 2θ))

y = π/2 – 2θ

y = π/2 – 2 tan ^-1 x

$\frac{dy}{dx} = \frac{(-2)}{(1 + x^2)}$

Pregunta 13. 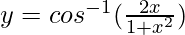$y = cos^{-1}(\frac{2x}{1+x^2})$ , -1 < x < 1

Solución:

Poner x = tanθ

θ = bronceado ^-1 x

y = cos^{-1}( $\frac{2tanθ}{1 + tan^2θ}$ )

y = cos ^-1 (sen 2θ)

y = cos ^-1 (cos (π/2 – 2θ))

y = π/2 – 2θ

y = π/2 – 2tan ^-1 x

$\frac{dy}{dx} = \frac{(-2)}{(1 + x^2)}$

Pregunta 14. 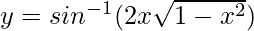$y = sin^{-1}(2x\sqrt{1-x^2})$ , -1/√2 < x < 1/√2

Solución:

Poner x = senθ

θ = sen ^-1 x

y = sen ^-1 (2senθ√(1 – sen ² θ))

y = sen ^-1 (sen 2θ) = 2θ

y = 2sen ^-1x

$\frac{dy}{dx} = \frac{2}{\sqrt{(1 - x^2)}}$

Pregunta 15. 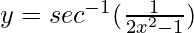$y = sec^{-1}(\frac{1}{2x^2-1})$ , 0 < x < 1/√2

Solución:

Poner x = tanθ

$y = sec^{-1}(\frac{1}{2 cos^2 - 1})$

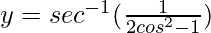
y = seg ^-1 (1/cos2θ))

y = seg ^-1 (sec2θ) = 2θ

y = 2 cos ^-1 x

$\frac{dy}{dx}$ = $\frac{-2}{\sqrt{1 - x^2} }$

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Encuentre lo siguiente:

Pregunta 1. 2x + 3y = sen x

Pregunta 2. 2x + 3y = sen y

Pregunta 3. ax + by 2 = cos y

Pregunta 4. xy + y 2 = tan x + y

Pregunta 5. x 2 + xy + y 2 = 100

Pregunta 6. x 3 + x 2 y + xy 2 + y 3 = 81

Pregunta 7. Sen 2 y + cos xy = π

Pregunta 8. sen 2 x + cos 2 y = 1

Pregunta 9. y = sen -1 (\frac{2x}{(1 + x 2 )}

Pregunta 10. , -1/√3 < x < 1/√3

Pregunta 11. , 0 < x < 1

Pregunta 12. , 0 < x < 1

Pregunta 13. , -1 < x < 1

Pregunta 14. , -1/√2 < x < 1/√2

Pregunta 15. , 0 < x < 1/√2

Deja una respuesta Cancelar la respuesta

Encuentre $\frac{dy}{dx}$ lo siguiente:

Pregunta 3. ax + by ² = cos y

Pregunta 4. xy + y ² = tan x + y

Pregunta 5. x ² + xy + y ² = 100

Pregunta 6. x ³ + x ² y + xy ² + y ³ = 81

Pregunta 7. Sen ² y + cos xy = π

Pregunta 8. sen ² x + cos ² y = 1

Pregunta 9. y = sen ^-1 (\frac{2x}{(1 + x ² )}

Pregunta 10. $Y=tan^{-1}\frac{(3x-x^3)}{(1-3x^2 )}$ , -1/√3 < x < 1/√3

Pregunta 11. $y = cos^{-1}(\frac{1-x^2}{1+x^2})$ , 0 < x < 1

Pregunta 12. $y = sin^{-1}(\frac{1-x^2}{1+x^2})$ , 0 < x < 1

Pregunta 13. $y = cos^{-1}(\frac{2x}{1+x^2})$ , -1 < x < 1

Pregunta 14. $y = sin^{-1}(2x\sqrt{1-x^2})$ , -1/√2 < x < 1/√2

Pregunta 15. $y = sec^{-1}(\frac{1}{2x^2-1})$ , 0 < x < 1/√2