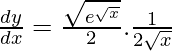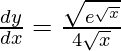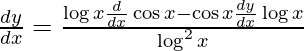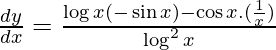Diferencie las siguientes wrt x
Pregunta 1. y = 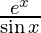
Solución:
(
)
Pregunta 2. 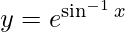
Solución:
Pregunta 3. 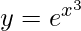
Solución:
Pregunta 4. y=sin(tan -1 e -x )
Solución:
Pregunta 5. y = log(cos e x )
Solución:
Pregunta 6.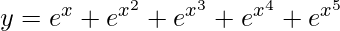
Solución:
Pregunta 7. 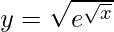
Solución:
Pregunta 8. y = log(log x)
Solución:
Pregunta 9. y = 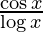
Solución:
Pregunta 10. y= cos (log x+e x )
Solución:
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA