Derive las funciones dadas en las preguntas 1 a 10 con respecto a x.
Pregunta 1. cos x.cos2x.cos3x
Solución:
Consideremos y = cos x.cos2x.cos3x
Ahora tomando registro en ambos lados, obtenemos
log y = log(cos x.cos2x.cos3x)
log y = log(cos x) + log(cos 2x) + log (cos 3x)
Ahora, al derivar wrt x, obtenemos
= -y(tan x + 2tan 2x + 3 tan 3x)
= -(cos x. cos 2x. cos 3x)(tan x + 2tan 2x + 3tan 3x)
Pregunta 2. 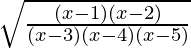
Solución:
Consideremos y =
Ahora tomando registro en ambos lados, obtenemos
registro y =
log y =
(log(x – 1)(x – 2)(x – 3)(x – 4)(x – 5))
log y =
(log(x – 1) + log(x – 2) – log(x – 3) – log(x – 4) – log(x – 5))
Ahora, al derivar wrt x, obtenemos
Pregunta 3. (log x) cos x
Solución:
Consideremos y = (log x) cos x
Ahora tomando registro en ambos lados, obtenemos
log y = log((log x) cos x )
log y = cos x(log(log x))
Ahora, al derivar wrt x, obtenemos
Pregunta 4. x x – 2 sen x
Solución:
Dado: y = x x – 2 sen x
Consideremos y = u – v
Donde, u = x x y v = 2 sen x
Entonces, dy/dx = du/dx – dv/dx ………(1)
Entonces primero tomamos u = x x
Al tomar el registro en ambos lados, obtenemos
registro u = registro x x
log u = x log x
Ahora, al derivar wrt x, obtenemos
du/dx = u(1 + log x)
du/dx = x x (1 + log x) ………(2)
Ahora tomamos v = 2 sen x
Al tomar el registro en ambos lados, obtenemos
log v = log (2 senx )
log v = sen x log2
Ahora, al derivar wrt x, obtenemos
dv/dx = v(log2cos x)
dv/dx = 2 sen x cos xlog2 ………(3)
Ahora ponga todos los valores de eq(2) y (3) en eq(1)
dy/dx = x x (1 + log x) – 2 sen x cos xlog2
Pregunta 5. (x + 3) 2 .(x + 4) 3 .(x + 5) 4
Solución:
Consideremos y = (x + 3) 2 .(x + 4) 3 .(x + 5) 4
Ahora tomando registro en ambos lados, obtenemos
logaritmo y = logaritmo[(x + 3) 3 .(x + 4) 3 .(x + 5) 4 ]
registro y = 2 registro (x + 3) + 3 registro (x + 4) + 4 registro (x + 5)
Ahora, al derivar wrt x, obtenemos
Pregunta 6. 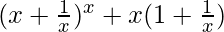
Solución:
Dado: y =
Consideremos y = u + v
donde
y
entonces, dy/dx = du/dx + dv/dx ………(1)
Ahora primero tomamos
Al tomar el registro en ambos lados, obtenemos
registro u =
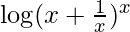
registro u =
Ahora, al derivar wrt x, obtenemos
………(2)
ahora tomamos
Al tomar el registro en ambos lados, obtenemos
registro v =
registro v =
Ahora, al derivar wrt x, obtenemos
………(3)
Ahora ponga todos los valores de eq(2) y (3) en eq(1)
Pregunta 7. (log x) x + x log x
Solución:
Dado: y = (log x) x + x log x
Consideremos y = u + v
Donde u = (log x) x y v = x log x
entonces, dy/dx = du/dx + dv/dx ………(1)
Ahora primero tomamos u = (log x) x
Al tomar el registro en ambos lados, obtenemos
registro u = registro (registro x) x
registro u = x registro (registro x)
Ahora, al derivar wrt x, obtenemos
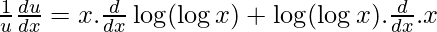
………(2)
Ahora tomamos v = x log x
Al tomar el registro en ambos lados, obtenemos
registro v = registro (x registro x )
log v = logx log(x)
registro v = logx 2
Ahora, al derivar wrt x, obtenemos
………(3)
Ahora ponga todos los valores de eq(2) y (3) en eq(1)
Pregunta 8. (sen x) x + sin –1 √x
Solución:
Dado: y = (sen x) x + sin –1 √x
Consideremos y = u + v
Donde u = (sen x) x y v = sen –1 √x
entonces, dy/dx = du/dx + dv/dx ………(1)
Ahora primero tomamos u = (sen x) x
Al tomar el registro en ambos lados, obtenemos
log u = log(sen x) x
log u = xlog(sen x)
Ahora, al derivar wrt x, obtenemos
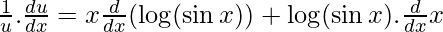
………(2)
Ahora tomamos v = sen –1 √x
Al tomar el registro en ambos lados, obtenemos
log v = log sen –1 √x
Ahora, al derivar wrt x, obtenemos
………(3)
Ahora ponga todos los valores de eq(2) y (3) en eq(1)
Pregunta 9. x sen x + (sen x) cos x
Solución:
Dado: y = x sen x + (sen x) cos x
Consideremos y = u + v
Donde u = x sen x y v = (sen x) cos x
entonces, dy/dx = du/dx + dv/dx ………(1)
Ahora primero tomamos u = x sin x
Al tomar el registro en ambos lados, obtenemos
log u = log x sen x
log u = sen x (log x)
Ahora, al derivar wrt x, obtenemos
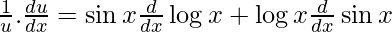
………(2)
Ahora tomamos v =(sen x) cos x
Al tomar el registro en ambos lados, obtenemos
log v = log(sen x) cos x
log v = cosx log(senx)
Ahora, al derivar wrt x, obtenemos
………(3)
Ahora ponga todos los valores de eq(2) y (3) en eq(1)
Pregunta 10. 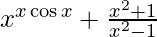
Solución:
Dado: y =
Consideremos y = u + v
Donde u = x xcosx y v =
entonces, dy/dx = du/dx + dv/dx ………(1)
Ahora primero tomamos u = x xcosx
Al tomar el registro en ambos lados, obtenemos
registro u = registro (x x cos x )
log u = x.cosx.logx
Ahora, al derivar wrt x, obtenemos
………(2)
Ahora tomamos v =
Al tomar el registro en ambos lados, obtenemos
registro v = registro
registro v = registro (x 2 + 1) – registro (x 2 – 1)
Ahora, al derivar wrt x, obtenemos
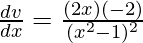
………(3)
Ahora ponga todos los valores de eq(2) y (3) en eq(1)
Capítulo 5 Continuidad y Diferenciabilidad – Ejercicio 5.5 | conjunto 2
Publicación traducida automáticamente
Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA