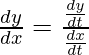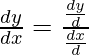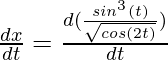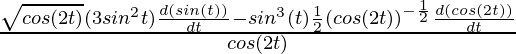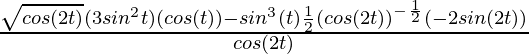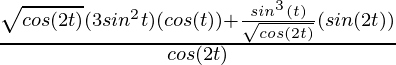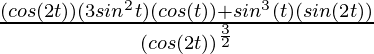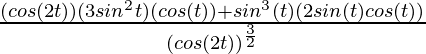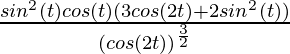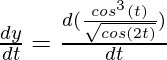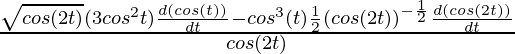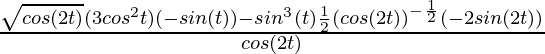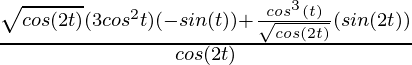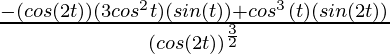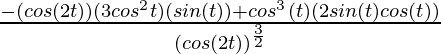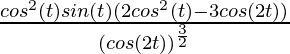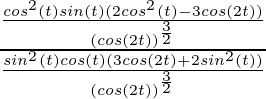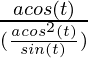Si x y y están conectados paramétricamente por las ecuaciones dadas en los ejercicios 1 a 10, sin eliminar el parámetro, encuentre 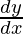
Pregunta 1. x = 2 en 2 , y = en 4
Solución:
Aquí, x = 2 en 2 , y = en 4
= 2a
= 2a (2t)
= 4 en
Y ahora
= un
= un (4t 3 )
= 4 a las 3
No fue
=
= t 2
Pregunta 2. x = a cos (θ) , y = b cos (θ)
Solución:
Aquí, x = a cos(θ), y = b cos(θ)
= un
= a (-sin(θ))
= – un sen(θ)
Y ahora
= segundo
= b (-sin(θ))
= – b sen(θ)
No fue
=
Pregunta 3. x = sin( t) , y = cos (2t)
Solución:
Aquí, x = sin(t), y = cos(2t)
= cos(t)
Y ahora
= -sen(2t)
= – 2sen(2t)
No fue
=
=
(Usando la identidad: sin(2θ) = 2 sinθ cosθ )
= – 4 sen(t)
Pregunta 4. x = 4t, y = 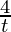
Solución:
Aquí, x = 4t, y = 4/t
= 4
= 4
Y ahora
= 4
= 4
= 4
= 4
=
No fue
=
Pregunta 5. x = cos (θ) – cos (2θ) , y = sen (θ) – sen (2θ)
Solución:
Aquí, x = cos(θ) – cos(2θ), y = sin(θ) – sin(2θ)
=
= – sin(θ) – (-sin(2θ))
= – sen(θ) + 2sen(2θ)
Y ahora
=
= cos(θ) – (cos(2θ))
= cos(θ) – (2 cos(2θ)
No fue
Pregunta 6. x = a (θ – sin (θ) ), y = a (1 + cos (θ) )
Solución:
Aquí, x = a (θ – sin(θ)), y = a (1 + cos(θ))
= un (
)
= a (1 – cos(θ))
Y ahora
= un (
)
= a (0 + (- sen (θ)))
= – un pecado (θ)
No fue
=
=
(Usando la identidad: sen(2θ) = 2 senθ cosθ y 1- cos(2θ) = 2 sen 2 θ )
= – cuna(θ/2)
Pregunta 7. x = 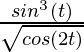 , y =
, y = 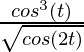
Solución:
Aquí, x =
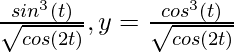
=
=
=
=
=
=
Y ahora
=
=
=
=
=
=
No fue
=
=
=
=
= – cuna 3(t)
Pregunta 8. x = a (cos (t) + log tan 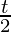 ), y = a sin( t)
), y = a sin( t)
Solución:
Aquí, x = a (cos(t) + log tan
), y = a sin(t)
= un (
)
= a (-sen(t) +
)
= a (-sen(t) +
)
= a (-sen(t) +
)
= a (-sen(t) +
)
= a (-sin(t) +
) (Usando la identidad: 2 sinθ cosθ = sin(2θ) )
= a (
– sin(t))
= un (
)
= un (
)
=
Y ahora
= un
= a cos(t)
No fue
=
= bronceado(t)
Pregunta 9. x = a seg (θ) , y = b tan (θ)
Solución:
Aquí, x = a seg(θ), y = b tan(θ)
= un (
)
= a (seg(θ) tan(θ))
= a seg(θ) tan(θ)
Y ahora
= segundo (
)
= b (seg 2 (θ))
No fue
Pregunta 10. x = a (cos (θ) + θ sin (θ) ), y = a (sin (θ) – θ cos (θ) )
Solución:
Aquí, x = a (cos(θ) + θ sin(θ)), y = a (sin(θ) – θ cos(θ))
= un (
)
= a (- sen(θ) + (θ.
) + sen(θ).
)
= a (- sen(θ) + (θ.(cos(θ) + sen(θ).1))
= a (- sen(θ) + θ cos(θ) + sen(θ))
= aθ cos(θ)
Y ahora
= un (
)
= a (cos (θ) – (θ.
) + cos(θ).
)
= a (cos(θ) – (θ.(-sen (θ) + cos(θ).1))
= a (cos(θ) + θ sen(θ) – cos(θ))
= aθ sen(θ)
No fue
=
= bronceado(θ)
Pregunta 11. Si x = 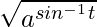 , y =
, y = 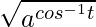 , demuestre que
, demuestre que 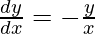
Solución:
Aquí, vamos a multiplicar x e y.
xy = (
)
= (
)
= (
) (Usando la identidad: sen -1 θ + cos -1 θ =
)
Diferenciemos wrt x,
X.
+ y.
= 0
X.
+ y = 0
Por lo tanto, Probado !!!
Publicación traducida automáticamente
Artículo escrito por _shinchancode y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA