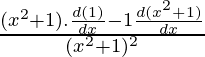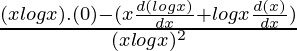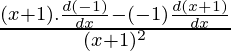Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 5 Continuidad y diferenciabilidad – Ejercicio 5.7

Encuentre las derivadas de segundo orden de las funciones dadas en los ejercicios 1 a 10.

Pregunta 1. x ² + 3x + 2

Solución:

Aquí, y = x ² + 3x + 2

Primera derivada,

$\frac{dy}{dx} = \frac{d(x^2+ 3x + 2)}{dx}$

= 2x+ 3

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(2x+3)}{dx}$

= 2

Pregunta 2. x ²⁰

Solución:

Aquí, y = x ²⁰

Primera derivada,

$\frac{dy}{dx} = \frac{d(x^{20})}{dx}$

= 20x ^20-1

= 20x ¹⁹

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(20x^{19})}{dx}$

= 20(19x ^19-1 )

= 380x ¹⁸

Pregunta 3. x. porque x

Solución:

Aquí, y = x. porque x

Primera derivada,

$\frac{dy}{dx} = \frac{d(x . cos x)}{dx}$

Usando la regla del producto

= x $\frac{d(cos x)}{dx}$ + cos x $\frac{d(x)}{dx}$

= x (-sen x)+ cos x (1)

= – x sen x+ cos x

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(- x sin x+ cos x)}{dx}$

= $\frac{d(- x sin x)}{dx} + \frac{d(cos x)}{dx}$

Usando la regla del producto,

= -x $\frac{d(sin x)}{dx}$ + sen x $\frac{d(-x)}{dx}$ + (- sen x)

= -x (cos x) + sen x (-1) – sen x

= – (x cos x + 2 sen x)

Pregunta 4. log x

Solución:

Aquí, y = log x

Primera derivada,

$\frac{dy}{dx} = \frac{d(log x)}{dx}$

= 1/x

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(1/x)}{dx}$

Usando la regla de división,

= $\frac{x \frac{d(1)}{dx} - 1\frac{d(x)}{dx}}{x^2}$

= $\frac{x (0) - 1(1)}{x^2}$

= $\mathbf {\frac{- 1}{x^2}}$

Pregunta 5. x ³ log x

Solución:

Aquí, y = x ³ . registro x

Primera derivada,

$\frac{dy}{dx} = \frac{d( x^3 log x)}{dx}$

Usando la regla del producto

= x ³ $\frac{d(log (x))}{dx}$ + registro x $\frac{d(x^3)}{dx}$

= x ³ ( $\frac{1}{x}$ ) + registro x (3x ² )

= x ² + 3x ² log x

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(x^2 + 3x^2 log x)}{dx}$

= $\frac{d(x^2)}{dx}$ + $\frac{d(3x^2 log x)}{dx}$

Usando la regla del producto,

= 2x + 3 (x ² $\frac{d(log (x))}{dx}$ – log x $\frac{d(x^2)}{dx}$ )

= 2x + 3 (x ² $\frac{1}{x}$ – registro x (2x))

= 2x + 3 (x – 2x . registro x)

= 2x + 3x – 6x . registro x

= x(5 – 6 registro x)

Pregunta 6. e ^x sen 5x

Solución:

Aquí, y = e ^x sen 5x

Primera derivada,

$\frac{dy}{dx} = \frac{d( e^x sin (5x))}{dx}$

Usando la regla del producto

= e ^x $\frac{d(sin (5x))}{dx}$ + sen 5x $\frac{d(e^x)}{dx}$

= e ^x (5 cos(5x))+ sen 5x (e ^x )

= e ^x (5 cos(5x)+ sen 5x)

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(e^x (5 cos(5x)+ sin 5x))}{dx}$

Usando la regla del producto,

= e ^x $\frac{d(5 cos(5x) + sin 5x)}{dx}$ + (5 cos(5x)+ sen 5x) $\frac{d(e^x)}{dx}$

= e ^x (5 (5(- sen 5x))) + 5(cos 5x) + (5 cos(5x)+ sen 5x) (e ^x )

= e ^x (- 25 sen 5x + 5cos 5x) + (5 cos(5x)+ sen 5x) (e ^x )

= e ^x (- 25 sen 5x + 5cos 5x + 5 cos(5x)+ sen 5x)

= e ^x (10 cos 5x – 24 sen 5x)

Pregunta 7. e ^6x cos 3x

Solución:

Aquí, y = e ^6x cos 3x

Primera derivada,

$\frac{dy}{dx} = \frac{d( e^{6x} cos (3x))}{dx}$

Usando la regla del producto

= e ^6x $\frac{d(cos (3x))}{dx}$ + cos 3x $\frac{d(e^{6x})}{dx}$

= e ^6x (- 3 sin(3x))+ cos 3x (6e ^6x )

= e ^6x (6 cos(3x) – 3 sen (3x))

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(e^{6x} (6 cos(3x) - 3 sin (3x)))}{dx}$

Usando la regla del producto,

= e ^6x ( $\frac{d(6 cos(3x) - 3 sin (3x))}{dx}$ ) + (6 cos(3x) – 3 sen (3x)) $\frac{d(e^{6x})}{dx}$

= e ^6x (6 (3 (- sen(3x)) – 3 (3 cos 3x)) + (6 cos(3x) – 3 sen (3x)) (6e ^6x )

= e ^6x (- 18 sen (3x) – 9 cos 3x) + (36 cos (3x) – 18 sen (3x)) (e ^6x )

= e ^6x (27 cos(3x) – 36 sen (3x))

= 9e ^6x (3 cos(3x) – 4 sen (3x))

Pregunta 8. bronceado ^–1 x

Solución:

Aquí, y = tan ^–1 x

Primera derivada,

$\frac{dy}{dx} = \frac{d( tan^{-1} x )}{dx}$

= $\frac{1}{x^2 + 1}$

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d}{dx}(\frac{1}{x^2 + 1})$

Usando la regla de división,

= $\frac{(x^2+1) . \frac{d(1)}{dx} - 1\frac{d(x^2+1)}{dx}}{(x^2+1)^2}$

= $\frac{(x^2+1) . (0) - (2x)}{(x^2+1)^2}$

= $\mathbf{\frac{- 2x}{(x^2+1)^2}}$

Pregunta 9. log (log x)

Solución:

Aquí, y = registro (registro x)

Primera derivada,

$\frac{dy}{dx} = \frac{d(log (log x))}{dx}$

= $\frac{1}{log x} \frac{d(log x)}{dx}$

= $\frac{1}{log x} . \frac{1}{x}$

= $\frac{1}{x log x}$

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d}{dx}(\frac{1}{x log x})$

Usando la regla de división,

= $\frac{(x log x) . \frac{d(1)}{dx} - 1\frac{d(x log x)}{dx}}{(x log x)^2}$

Usando la regla del producto,

= $\frac{(x log x) . (0) - (x \frac{d(log x)}{dx} + log x \frac{d(x)}{dx})}{(x log x)^2}$

= – $\frac{ (x \frac{1}{x} + log x (1)}{(x log x)^2}$

= – $\frac{(1 + log x)}{(x log x)^2}$

= – $\mathbf{\frac{1 + log x}{(x log x)^2}}$

Pregunta 10. sen (log x)

Solución:

Aquí, y = sen (log x)

Primera derivada,

$\frac{dy}{dx} = \frac{d(sin (log (x)))}{dx}$

= cos (log x) $\frac{d(log (x))}{dx}$

= cos (log x) . $\frac{1}{x}$

= $\frac{ cos (log (x))}{x}$

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d}{dx}(\frac{ cos (log (x))}{x})$

Usando la regla de división,

= $\frac{x . \frac{d(cos (log x))}{dx} - cos (log x)\frac{d(x)}{dx}}{x ^2}$

= $\frac{x . (- sin(log x) . \frac{d(log x)}{dx}) - cos (log x)(1)}{x ^2}$

= $\frac{x . (- sin(log x) . \frac{1}{x}) - cos (log x)}{x ^2}$

= $\mathbf{\frac{- sin(log (x)) - cos (log (x))}{x ^2}}$

Pregunta 11. Si y = 5 cos x – 3 sen x, prueba que 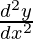$\frac{d^2y}{dx^2}$ + y = 0

Solución:

Aquí, y = 5 cos x – 3 sen x

Primera derivada,

$\frac{dy}{dx} = \frac{d(5 cos x - 3 sin x)}{dx}$

= 5 (- sen x) – 3 (cos x)

= – 5 sen(x) – 3 cos(x)

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(- 5 sin(x) - 3 cos(x))}{dx}$

= $\frac{d(- 5 sin(x))}{dx} - \frac{d(3 cos(x))}{dx}$

= -5 (cos(x)) – 3 (- sen(x))

= -(5 cos(x) – 3 sen(x))

= -y

Según la condición dada,

$\frac{d^2y}{dx^2}$ + y = -y + y

$\mathbf{\frac{d^2y}{dx^2}}$ + y = 0

Por lo tanto Probado !!

Pregunta 12. Si y = cos ^-1 x, encuentre 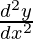$\frac{d^2y}{dx^2}$ en términos de y solo.

Solución:

Aquí, y = cos-1 x

x = cos y

Primera derivada,

$\frac{dx}{dy} = \frac{d(cos y)}{dy}$

= – sen y

$\frac{dy}{dx} = \frac{-1}{sin (y)}$

= – cosec (y)

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d(- cosec (y))}{dx}$

= – (-cosec(y) cuna(y)) $\frac{dy}{dx}$

= – (-cosec(y) cot (y)) (-cosec(y))

= -cosec ² (y) cot (y)

Por lo tanto, obtenemos

$\mathbf{\frac{d^2y}{dx^2}}$ = -cosec ² (y) cot (y)

Pregunta 13. Si y = 3 cos (log x) + 4 sin (log x), demuestre que x ² y ₂ + xy ₁ + y = 0

Solución:

Aquí, y = 3 cos (log x) + 4 sin (log x)

Primera derivada,

y ₁ = $\frac{dy}{dx} = \frac{d(3 cos (log x) + 4 sin (log x))}{dx}$

= 3 (-sen (log x)) $\frac{d(log(x))}{dx}$ + 4 (cos (log (x))) $\frac{d(log(x))}{dx}$

= $\frac{1}{x}$ (4 cos (log(x)-3 sen (log x))

Segunda derivada,

y ₂ = $\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d}{dx} (\frac{1}{x} (4 cos (log(x)-3 sin (log x)))$

Usando la regla del producto.

= $\frac{1}{x}$ $\frac{d}{dx}(4 cos (log(x)-3 sin (log x)) + (4 cos (log(x)-3 sin (log x)) \frac{d}{dx} (\frac{1}{x})$

= $\frac{1}{x}$ (4(-sen(log(x))) $\frac{1}{x}$ – 3 (cos(log(x))) ) $\frac{1}{x}$ + (4 cos(log(x)-3 sen (log x)) ( $\frac{1}{x^2}$ )

= $\frac{1}{x}$ (-4sen(log(x)) $\frac{1}{x}$ – 3 coseno(log(x)) $\frac{1}{x}$ ) – (4 coseno(log(x) + 3 sen (log x)) ( $\frac{1}{x^2}$ )

= \frac{-1}{x^2} [-7 cos(log(x) – sin (log x)]

Según las condiciones dadas,

xy ₁ = x( $\frac{1}{x}$ (4 cos (log(x)-3 sen (log x)))

xy ₁ = -3 sen (log x)+ 4 cos (log(x))

x ² y ₂ = x ² $(\frac{1}{x^2} [-7 cos(log(x) - sin (log x)])$

x ² y ₂ =[-7 cos(log(x) – sen (log x)]

Ahora, reorganizando

xy ₁ + x ² y ₂ + y = -3 sen (log x)+ 4 cos (log(x)) + cos(log(x)) -7 cos(log(x) – sen (log x) + 4 sen (log x)

Por lo tanto, obtenemos

xy ₁ + x ² y ₂ + y = 0

Pregunta 14. Si y = Ae ^mx + Be ^nx , demuestre que 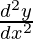$\frac{d^2y}{dx^2}$ – (m+n) $\frac{dy}{dx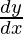}$ + mny = 0.

Solución:

Aquí, y = Ae ^mx + Be ^nx

Primera derivada,

$\frac{dy}{dx} = \frac{d(Ae^{mx} + Be^{nx})}{dx}$

= mAe ^mx + nBe ^nx

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d}{dx}(mAe^{mx} + nBe^{nx})$

= m ² Ae ^mx + n ² Be ^nx

Según las condiciones dadas,

$\frac{d^2y}{dx^2}$ – (m+n) $\frac{dy}{dx}$ + mny, obtenemos

LHS = m ² Ae ^mx + n ² Be ^nx – (m+n)(mAe ^mx + nBe ^nx ) + mny

= m ² Ae ^mx + n ² Be ^nx – (m ² Ae ^mx + mnAe ^mx + mnBe ^nx + n ² Be ^nx ) + mny

= -(mnAe ^mx + mnBe ^nx ) + mny

= -mny + mny

= 0

Por lo tanto, obtenemos

$\mathbf{\frac{d^2y}{dx^2} - (m+n) \frac{dy}{dx}}$ + mucho = 0

Pregunta 15. Si y = 500e ^7x + 600e ^{– 7x} , demuestre que 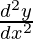$\frac{d^2y}{dx^2}$ = 49y.

Solución:

Aquí, y = 500e ^7x + 600e ^{– 7x}

Primera derivada,

$\frac{dy}{dx} = \frac{d(500e^{7x}+ 600e^{- 7x})}{dx}$

= 500e ^7x . (7)+ 600e ^{– 7x} (-7)

= 7(500e ^7x – 600e ^{– 7x} )

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d}{dx}(7(500e^{7x} - 600e^{- 7x}))$

= 7[500e ^7x . (7) – 600e ^{– 7x} . (-7)]

= 49[500e ^7x + 600e ^{– 7x} ]

= 49 años

Por lo tanto Probado !!

Pregunta 16. Si e ^y (x + 1) = 1, demuestre que 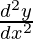$\frac{d^2y}{dx^2}$ = $(\frac{dy}{dx})^2$

Solución:

e ^y (x + 1) = 1

e ^-y = (x+1)

Primera derivada,

$\frac{d(e^{-y})}{dx} = \frac{d(x+1)}{dx}$

-e ^-y $\frac{dy}{dx}$ = 1

$\frac{dy}{dx} = \frac{-1}{e^{-y}}$

= $\frac{-1}{(x+1)}$

Segunda derivada,

$\frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx})$

= $\frac{d}{dx}(\frac{-1}{(x+1)})$

Usando la regla de división,

= $\frac{(x+1) . \frac{d(-1)}{dx} - (-1)\frac{d(x+1)}{dx}}{(x+1) ^2}$

= $\frac{(x+1) . (0) + (1)}{(x+1) ^2}$

= $\frac{1}{(x+1) ^2}$

= $(\frac{-1}{(x+1)})^2$

Por lo tanto podemos concluir que,

$\mathbf{\frac{d^2y}{dx^2} = (\frac{dy}{dx})^2}$

Pregunta 17. Si y = (tan ^–1 x) ² , demuestre que (x ² + 1) ² y ₂ + 2x (x ² + 1) y ₁ = 2

Solución:

Aquí, y = (tan–1 x) ²

$\frac{dy}{dx} = \frac{d((tan-1 x)^2)}{dx}$

= 2 . bronceado–1 x $\frac{1}{x^2 + 1}$

(x ² + 1) $\frac{dy}{dx}$ = 2 tan–1 x

Derivación adicional,

( ^x2 + 1) $\frac{d^2y}{dx^2}$ + $\frac{dy}{dx} \frac{d}{dx}$ (x2 + 1) = $\frac{d}{dx}(2 tan^{-1} x)$

(x ² + 1) $\frac{d^2y}{dx^2}$ + $\frac{dy}{dx}$ (2x) = 2 $\frac{1}{x^2+1}$

Multiplicando (x ² + 1),

( ^x2 + 1) ² $\frac{d^2y}{dx^2}$ + $\frac{dy}{dx}$ (2x)(x2 ⁺ 1) = 2

Por lo tanto probado,

(x ² + 1) ² y ₂ + 2x (x ² + 1) y ₁ = 2

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Encuentre las derivadas de segundo orden de las funciones dadas en los ejercicios 1 a 10.

Pregunta 1. x 2 + 3x + 2

Pregunta 2. x 20

Pregunta 3. x. porque x

Pregunta 4. log x

Pregunta 5. x 3 log x

Pregunta 6. e x sen 5x

Pregunta 7. e 6x cos 3x

Pregunta 8. bronceado –1 x

Pregunta 9. log (log x)

Pregunta 10. sen (log x)

Pregunta 11. Si y = 5 cos x – 3 sen x, prueba que + y = 0

Pregunta 12. Si y = cos -1 x, encuentre en términos de y solo.

Pregunta 13. Si y = 3 cos (log x) + 4 sin (log x), demuestre que x 2 y 2 + xy 1 + y = 0

Pregunta 14. Si y = Ae mx + Be nx , demuestre que – (m+n) + mny = 0.

Pregunta 15. Si y = 500e 7x + 600e – 7x , demuestre que = 49y.

Pregunta 16. Si e y (x + 1) = 1, demuestre que =

Pregunta 17. Si y = (tan –1 x) 2 , demuestre que (x 2 + 1) 2 y 2 + 2x (x 2 + 1) y 1 = 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. x ² + 3x + 2

Pregunta 2. x ²⁰

Pregunta 5. x ³ log x

Pregunta 6. e ^x sen 5x

Pregunta 7. e ^6x cos 3x

Pregunta 8. bronceado ^–1 x

Pregunta 11. Si y = 5 cos x – 3 sen x, prueba que $\frac{d^2y}{dx^2}$ + y = 0

Pregunta 12. Si y = cos ^-1 x, encuentre $\frac{d^2y}{dx^2}$ en términos de y solo.

Pregunta 13. Si y = 3 cos (log x) + 4 sin (log x), demuestre que x ² y ₂ + xy ₁ + y = 0

Pregunta 14. Si y = Ae ^mx + Be ^nx , demuestre que $\frac{d^2y}{dx^2}$ – (m+n) $\frac{dy}{dx}$ + mny = 0.

Pregunta 15. Si y = 500e ^7x + 600e ^{– 7x} , demuestre que $\frac{d^2y}{dx^2}$ = 49y.

Pregunta 16. Si e ^y (x + 1) = 1, demuestre que $\frac{d^2y}{dx^2}$ = $(\frac{dy}{dx})^2$

Pregunta 17. Si y = (tan ^–1 x) ² , demuestre que (x ² + 1) ² y ₂ + 2x (x ² + 1) y ₁ = 2