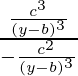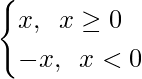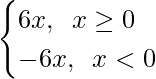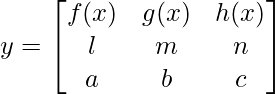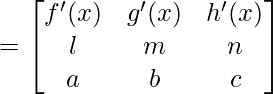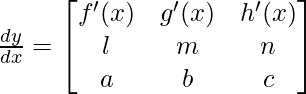Diferenciar wrt x la función en el Ejercicio 1 al 11.
Pregunta 1. (3 x 2 – 9x – 5) 9
Solución:
Supongamos y = (3x 2 – 9x – 5) 9
Ahora, diferencie wrt x
Usando la regla de la string, obtenemos
= 9(3x 2 – 9x + 5) 8
= 9(3x 2 – 9x + 5) 8 .(6x – 9)
= 9(3x 2 – 9x + 5) 8 .3(2x – 3)
= 27(3x 2 – 9x + 5) 8 (2x – 3)
Pregunta 2. sen 3 x + cos 6 x
Solución:
Supongamos y = sen 3 x + cos 6 x
Ahora, diferencie wrt x
Usando la regla de la string, obtenemos
=
=
= 3 sen 2 x. cos x + 6 cos 5 x.(-sen x)
= 3 sen x cos x (sen x – 2 cos 4 x)
Pregunta 3. 5x 3 cos 2 x
Solución:
Supongamos y = 5x 3 cos 2x
Ahora estamos tomando logaritmo en ambos lados
logía = 3 cos 2 x log 5 x
Ahora, diferencie wrt x
Pregunta 4. sen -1 (x√x), 0 ≤ x ≤ 1
Solución:
Supongamos y = sen -1 (x√x)
Ahora, diferencie wrt x
Usando la regla de la string, obtenemos
=
=
=
=
=
Pregunta 5. 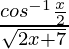 ,-2 < x < 2
,-2 < x < 2
Solución:
Supongamos y =
Ahora, derivar wrt x y por la regla del cociente, obtenemos
=
=
=
=
Pregunta 6. 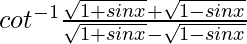 , 0 < x < π/2
, 0 < x < π/2
Solución:
Supongamos y =
……(1)
ahora resuelve
=
=
=
=
=
= cox/2
Ahora ponga este valor en la ecuación (1), obtenemos
y = cuna -1 (cotx/2)
y = x/2
Ahora, diferencie wrt x
dy/dx = 1/2
Pregunta 7. (log x) log x , x > 1
Solución:
Supongamos y = (log x) log x
Ahora estamos tomando logaritmos en ambos lados,
registro y = registro x . registro (registro x)
Ahora, diferencie wrt x en ambos lados, obtenemos
Pregunta 8. cos(a cos x + b sen x), para alguna constante a y b.
Solución:
Supongamos y = cos(a cos x + b sen x)
Ahora, diferencie wrt x
Usando la regla de la string, obtenemos
= -sen x(a cos x + b sen x).[a (-sen x) + b cos x]
= (a sen x – b cos x). sen (a cos x + b sen x)
Pregunta 9. (sen x – cos x) (sen x – cos x) , π/4 < x < 3π/4
Solución:
Supongamos y = (sen x – cos x) (sen x – cos x)
Ahora estamos tomando logaritmos en ambos lados,
log y = (sen x – cos x).log(sen x – cos x)
Ahora, diferencie wrt x, obtenemos
Usando la regla de la string, obtenemos
dy/dx = (senx – cosx) (senx – cosx) [(cosx + senx).log(senx – cosx) + (cosx + senx)]
dy/dx = (senx – cosx) (senx – cosx) (cosx + senx)[1 + log (senx – cosx)]
Pregunta 10. x x + x a + a x + a a para algunos fijos a > 0 y x > 0
Solución:
Supongamos y = x x + x a + a x + a a
Además, supongamos que x x = u, x a = v, a x = w, a a = s
Por lo tanto, y = u + v + w + s
Entonces, al diferenciar wrt x, obtenemos
……….(1)
Entonces primero resolvemos: u = x x
Ahora estamos tomando logaritmos en ambos lados,
registro u = registro x x
log u = x log x
Al diferenciar ambos lados de x, obtenemos
du/dx = x x [logx + 1] = x x (1 + logx) …….(2)
Ahora resolvemos: v = x a
Al diferenciar ambos lados de x, obtenemos
dv/dx = hacha (a – 1) ……(3)
Ahora resolvemos: w = a x
Ahora estamos tomando logaritmos en ambos lados,
log w = log a x
log w = x log a
Al diferenciar ambos lados de x, obtenemos
dw/dx = w loga
dw/dx = ax loga ………(4)
Ahora resolvemos: s = a a
Entonces, al diferenciar wrt x, obtenemos
ds/dx = 0 ………(5)
Ahora ponga todos estos valores de eq(2), (3), (4), (5) en eq(1), obtenemos
dy/dx = x x (1 + logx) + ax (a – 1) + a x loga + 0
= x x (1 + log x) + ax a -1 + a x log a
Pregunta 11. Diferenciar wrt x, 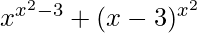 , para x > 3
, para x > 3
Solución:
Supongamos y =
También consideremos u =
y v =
entonces, y = tu + v
Al diferenciar ambos lados de x, obtenemos
…….(1)
Entonces, ahora resolvemos, u =
Ahora estamos tomando logaritmos en ambos lados,
registro u = registro
log u = (x 2 – 3) log x
Al derivar wrt x, obtenemos
=
…….(2)
Ahora resolvemos: v =
Ahora estamos tomando logaritmos en ambos lados,
registro v =
registro v = x 2 registro (x – 3)
Al diferenciar ambos lados de x, obtenemos
…..(3)
Ahora ponga todos estos valores de eq(2), y (3) en eq(1), obtenemos
Pregunta 12. Encuentra dy/dx , si y = 12(1 – cos t), x = 10 (t – sin t), -π/2 < t < π/2
Solución:
Según la pregunta
y = 12(1 – cos t) ……(1)
x = 10 (t – sen t) ……(2)
Entonces, \frac{dy}{dx}= \frac{\frac{dy}{dt}}{\frac{dx}{dt}} ……(3)
Al diferenciar la ecuación (1) con t, obtenemos
![Rendered by QuickLaTeX.com \frac{dy}{dt} = \frac{d}{dt} [12 (1 - cost)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9ded82de7bbd4396c457999d2ac6ccdf_l3.png)
=
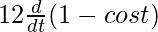
= 12.[0 – (- sen t)]
= 12 sen t
Al diferenciar la ecuación (2) con t, obtenemos
![Rendered by QuickLaTeX.com \frac{dx}{dt}=\frac{d}{dt}[10. (t - sin t)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a8fc9a390561b4777c023ccf46cef5b0_l3.png)
=
= 10(1 – cos t)
Ahora ponga el valor de dy/dt y dx/dt en la ecuación (3), obtenemos
=
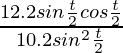
= 6/5 cuna t/2
Pregunta 13. Halla dy/dx, si y = sen -1 x + sen -1 √1-x 2 , 0 < x < 1
Solución:
Según la pregunta
y = sen -1 x + sen -1 √1 – x 2
Al derivar wrt x, obtenemos
Usando la regla de la string, obtenemos
=
=
=
=
dy/dx = 0
Pregunta 14. Si x√1 + y + y√1 + x = 0, para -1 < x < 1, prueba que 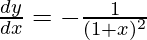
Solución:
Según la pregunta
x√1 + y = -y√1 + x
Al elevar al cuadrado ambos lados, obtenemos
x2 ( 1 + y) = y2 ( 1 + x)
⇒ x 2 + x 2 y = y 2 + xy 2
⇒ x 2 – y 2 = xy 2 – x 2 y
⇒ x 2 – y 2 = xy (y – x)
⇒ (x + y)(x – y) = xy (y – x)
⇒ x + y = -xy
⇒ (1 + x) y = -x
⇒ y = -x/(1 + x)
Al diferenciar ambos lados de x, obtenemos
=
=
Por lo tanto probado.
Pregunta 15. Si (x – a) 2 + (y – b) 2 = c 2 , para alguna c > 0, demuestre que ![Rendered by QuickLaTeX.com \frac{[1+(\frac{dy}{dx})^2]^\frac{3}{2}} {\frac{d^2y}{dx^2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-332cb28f2a10cef087f8c053cab15b63_l3.png) es una constante independiente de a y b.
es una constante independiente de a y b.
Solución:
Según la pregunta
(x – a) 2 + (y – b) 2 = c 2
Al diferenciar ambos lados de x, obtenemos
⇒ 2(x – a).
+ 2(y – b)
= 0
⇒ 2(x – a).1 + 2(y – b).
= 0
⇒
…….(1)
Nuevamente, al diferenciar ambos lados con respecto a x, obtenemos
…….[De la ecuación (1)]
=
=
=
= – c, que es constante e independiente de a y b.
Por lo tanto probado.
Pregunta 16. Si cos y = x cos (a + y), con cos a ≠ ±1, demuestre que 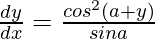
Solución:
Según la pregunta
cos y = x cos (a + y)
Al diferenciar ambos lados de x, obtenemos
=
![Rendered by QuickLaTeX.com \frac{d}{dx}[x cos(a + y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-12daf24fe228c934b29b610860b9ce3c_l3.png)
⇒ – sen y dy/dx = cos (a + y).
+ x
![Rendered by QuickLaTeX.com \frac{d}{dx}[cos (x+y)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20bad57f0d3235b66d516530c0c9ffcb_l3.png)
⇒ – sen y dy/dx = cos (a + y) + x [-sen (a + y)]dy/dx
⇒ [x sen (a + y) – sen y] dy/dx = cos (a + y) ……..(1)
Como cos y = x cos (a + y), x =
Ahora podemos reducir la ecuación (1)
= cos(a + y)
⇒ [cos y.sen (a + y)- sen y.cos (a + y)].dy/dx = cos 2 (a + y)
⇒ sin(a + y – y)dy/dx = cos 2 (a + b)
⇒
Por lo tanto probado.
Pregunta 17. Si x = a (cos t + t sen t) y y = a (sen t – t cos t), encuentre 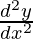
Solución:
Según la pregunta
x = a (cos t + t sen t) …..(1)
y = a (sen t – t cos t) …..(2)
Entonces, \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}} …..(3)
Al diferenciar la ecuación (1) con t, obtenemos
dx/dt = a.
Usando la regla de la string, obtenemos
= a[-sen t +sen t.
+ T.
]
= a [-sen t + sin t + t cos t]
= al costo t
Al diferenciar la ecuación (2) con t, obtenemos
dy/dt = a.
Usando la regla de la string, obtenemos
= a [costo t – [costo.
+ T.
]]
= a[cos t – {cos t – t sen t}]
= en sen t
Ahora ponga los valores de dx/dt y dy/dt en eq(1), obtenemos
dy/dx = en sen t/en cos t = tan t
Nuevamente, diferenciando ambos lados de x, obtenemos
=
= seg 2 t.
= seg 2 t.
……..[dx/dt = al costo ⇒ dt/dx = 1/al costo]
= seg 3 t/en
Pregunta 18. Si f(x) = |x| 3 , demuestre que f”(x) existe para todo x real y encuéntrelo.
Solución:
Como sabemos que |x| =
Entonces, cuando x ≥ 0, f(x) = |x| 3 = x 3
Entonces, al diferenciar ambos lados de x, obtenemos
f'(x) = 3x 2
De nuevo, diferenciando ambos lados de x, obtenemos
f”(x) = 6x
Cuando x < 0, f(x) = |x| 3 = -x 3
Entonces, al diferenciar ambos lados de x, obtenemos
f'(x) = – 3x 2
De nuevo, diferenciando ambos lados de x, obtenemos
f”(x) = -6x
Entonces, para f(x) = |x| 3 , f”(x) existe para todo x real, y está dada por
f”(x) =
Pregunta 19. Usando inducción matemática, demuestre que 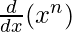 = (nx) n – 1 para todos los números enteros positivos n.
= (nx) n – 1 para todos los números enteros positivos n.
Solución:
Entonces, P(n) =
= (nx) n – 1
Para n = 1:
P(1) :
= (1x)1 – 1 =1
Por lo tanto, P(n) es cierto para n = 1
Consideremos que P(k) es cierto para algún entero positivo k.
Entonces, P(k):
= (kx) k – 1
Para P(k + 1):
= ((k + 1)x) (k + 1) – 1
x k
+ x.
….(Usando la regla del producto aplicado)
= x k .1 + x . k xk -1
= xk + kxk
= (k + 1) x k
= (k + 1) x (k + 1) – 1
Por lo tanto, P(k+1) es verdadero siempre que P(k) sea verdadero.
Entonces, según el principio de inducción matemática, P(n) es cierto para todo número entero positivo n.
Por lo tanto probado.
Pregunta 20. Utilizando el hecho de que sen(A + B) = sen A cos B + cos A sen B y la diferenciación, obtenga la fórmula de suma de cosenos.
Solución:
Según la pregunta
sen(A + B) = sen A cos B + cos A sen B
Al diferenciar ambos lados de x, obtenemos
=
+
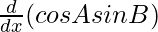
⇒ porque (A + B).
= cos B.
+ sen A.
+ sen B.
+ cos A.
⇒ coseno (A+B).
= cos B.cos A
+ sin A (-sin B)
+ sin B (-sin A).
+ cos A cos B
⇒ porque (A + B).
=(cos A cos B – sen A sen B).
Por tanto, cos (A + B) = cos A cos B – sen A sen B
Pregunta 21. ¿Existe una función que sea continua en todas partes pero no diferenciable exactamente en dos puntos? Justifica tu respuesta.
Solución:
Consideremos una función f dada como
f(x) = |x – 1| + |x – 2|
Como ya sabemos que las funciones de módulo son continuas en todos los puntos
Entonces, la suma también es continua en todos los puntos pero no diferenciable en todos los puntos x = 0
Sea x = 1, 2
Ahora en x = 1
LHD = límite x⇢ 1 –
LHD = límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= -2
RHD = límite x⇢1 +
RHD = límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= límite h⇢0
= 0
Desde LHD ≠ RHD
Entonces, dada la función f no es diferenciable en x = 1.
De manera similar, obtenemos que la función dada no es diferenciable en x = 2.
Por lo tanto, existe una función que es continua en todas partes pero no diferenciable exactamente en dos puntos.
Pregunta 22. Si 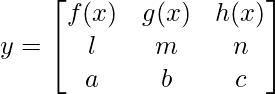 prueba que
prueba que 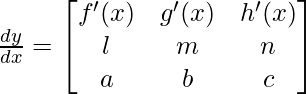
Solución:
Dado que
⇒ y =(mc – nb) f(x)- (lc – na )g(x) +(lb – ma) h(x)
[(mc -nb) f(x)] –
[(lc – na) g(x)] +
[(lb – ma) h(x)]
= (mc – nb) f'(x) – (lc – na) g'(x) + (lb – ma ) h’ (x)
Asi que,
Por lo tanto probado.
Pregunta 23. Si y = 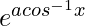 ,-1 ≤ x ≤ 1, demuestre que
,-1 ≤ x ≤ 1, demuestre que 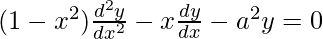
Solución:
Según la pregunta
y =
Ahora estamos tomando logaritmos en ambos lados,
log y = a cos -1 x log e
log y = a cos -1 x
Al diferenciar ambos lados de x, obtenemos
⇒
Al elevar al cuadrado ambos lados, obtenemos
⇒(1-x 2 )
=a 2 y 2
Al derivar nuevamente ambos lados frente a x, obtenemos
⇒
⇒
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por ritikasharma23 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
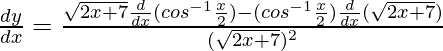
![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}[\frac{-1}{\sqrt{1-(\frac{x}{2})^2}}.\frac{d}{dx}(\frac{x}{2})]-(cos^{-1}\frac{x}{2})\frac{1}{2\sqrt{2x+7}}.\frac{d}{dx}(2x+7)}{2x+\frac{7}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-928ac7ece6a1ec001eba42741795774e_l3.png)
![Rendered by QuickLaTeX.com \frac{\sqrt{2x+7}\frac{-1}{\sqrt{4-x^2}}-[cos^{-1}\frac{x}{2}]\frac{2}{2\sqrt{2x+7}}}{2x+7}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5482b8d0de56fb7d74a6c4bd5e28cc2f_l3.png)
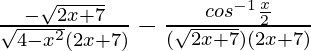
![Rendered by QuickLaTeX.com -[\frac{1}{\sqrt{4-x^2}\sqrt{2x+7}}+\frac{cos^{-1}\frac{x}{2}}{(2x+7)^\frac{1}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ff2ddba68516f46c431046b166484041_l3.png)
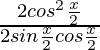
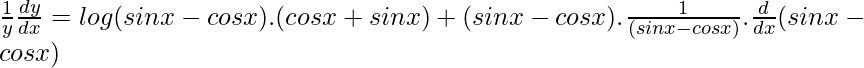
![Rendered by QuickLaTeX.com =-[\frac{(y-b)-(x-a).\frac{dy}{dx}}{(y-b)^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-55457f6e8f9b90f73a06e8b7ab021d13_l3.png)
![Rendered by QuickLaTeX.com [\frac{1+[\frac{dy}{dx}]^2}{\frac{d^2y}{dx^2}}]^{\frac{3}{2}}= \frac{[1+\frac{(x-a)^2}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2 + (x-a)^2}{(y-b)^3}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-018d25e7407f1a0978d4fe72befce076_l3.png)
![Rendered by QuickLaTeX.com \frac{[\frac{[(y-b)^2+(x-a)^2]}{(y-b)^2}]^{\frac{3}{2}}}{-[\frac{(y-b)^2+(x-a)^2}{(y-b)^3}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-47c73e07695be04410c04dacb47abe07_l3.png)
![Rendered by QuickLaTeX.com \frac{[\frac{c^2}{(y-b)^2}]\frac{3}{2}}{-\frac{c^2}{(y-b)^3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-52915b2ff0ab706529a3c46883284d7b_l3.png)