Soluciones NCERT Clase 12 – Matemáticas Parte I – Capítulo 6 Aplicación de Derivadas – Ejercicio 6.3

Capítulo 6 Aplicación de Derivadas -Ejercicio 6.3 | Serie 1

Pregunta 14. Encuentra las ecuaciones de la tangente y normal a las curvas dadas en los puntos indicados:

(i) y = x ⁴ – 6x ³ + 13x ² – 10x+ 5 en (0, 5)

(ii) y = x ⁴ – 6x ³ + 13x ² – 10x + 5 en (1, 3)

(iii) y = x ³ en (1, 1)

(iv) y = x ² en (0, 0)

(v) x = cos t, y = sen t en t = π/4

Solución:

(i) Curva dada

y = x ⁴ – 6x ³ + 13x ² – 10x + 5

Punto dado, (0, 5)

dy/dx = 4x ³ – 18x ² + 26x – 10

dy/dx = 4(0) ³ – 18(0) ² + 26(0) – 10

dy/dx = -10,

-dx/dy = 1/10

Ahora, con la ayuda de la forma de pendiente de puntos

y – y ₁ = m(x – x ₁ )

y-5 = -10(x-0)

y + 10x = 5 es la ecuación requerida de la tangente

Para la ecuación de la normal,

y – y1 = $\frac{-dx}{dy}(x-x_1)$

y-5 = $\frac{1}{10}(x-0)$

10y – x – 50 es la ecuación de la normal.

(ii) Curva dada: y = x ⁴ – 6x ³ + 13x ² – 10x + 5

El punto dado es (1, 3)

dy/dx = 4x ³ – 18x ² + 26x – 10

dy/dx = 4(1) ³ – 18(1) ² + 26(1) – 10

dy/dx = 4 – 18 + 26 – 10 = 2

dy/dx = 2

-dx/dy = -1/2

Usando la forma de punto pendiente, la ecuación de la tangente es

y – y ₁ = dy/dx(x – x1)

y-3 = 2(x-1)

y – 2x = 1 es la ecuación de la tangente.

Usando la forma punto pendiente, la ecuación de la normal es

y – y ₁ = -dx/dy(x – 1)

y-3 = -1/2(x-1)

2y – 6 = -x + 1

2y + x = 7 es la ecuación de la normal.

(iii) Curva dada: y = x ³

El punto dado es (1, 1)

dy/dx = 3x ²

dy/dx = 3(1) ² = 3

dy/dx = 3 & -dx/dy = -1/3

Usando la forma de punto pendiente, la ecuación de la tangente es y – y ₁ = dy/dx(x – x ₁ )

y – y ₁ = dy/dx(x – x ₁ )

y-1 = 3(x-1)

y – 3x + 2 = 0 es la ecuación de la tangente

Usando la forma punto pendiente, la ecuación de la normal es

y – y1 = $\frac{-dx}{dy}(x-x_1)$

y-1 = $\frac{-1}{3}(x-1)$

3y – 3 = -x + 1

3y + x = 4 es la ecuación de la normal.

(iv) Curva dada: y = x ²

Punto dado (0, 0)

dy/dx = 2x

dy/dx = 0

dy/dx = 0 & -dx/dy = no definido es

y – y ₁ = dy/dx(x – x ₁ )

y-0 = 0(x-0)

y = 0 es la ecuación de la tangente.

Usando la forma punto pendiente, la ecuación de la normal es

y – y ₁ = $\frac{-dx}{dy}(x-x_1)$ -(1)

-dx\dy no está definido, por lo que podemos escribir eq(1) como

$\frac{-dy}{dx}(y-y_1)=x-x_1$

Ahora poniendo dy/dx = 0 obtenemos

0(y – 0) = x-0

x = 0 es la ecuación de la normal.

(v) Ecuación de la curva: x = cos t y y = sen t

Punto t = π/4

$\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$ -(1)

$\frac{dx}{dt}=\frac{d(\cos t)}{dt}=-\sin t$

$\frac{dy}{dt}=\frac{d(\sin t)}{dt}=\cos t$

Al poner estos valores en la ecuación (1), obtenemos

$\frac{dy}{dx}=\frac{\cos t}{-\sin t}=-\cot t$

$\frac{dy}{dx}=-\cot \frac{π}{4}=-1$

dy/dx = -1 y -dx/dy = 1

Ahora para t = π/4,

y ₁ = sen t = sen( π/4 ) = 1/√2

x ₁ = cos t = cos( π/4 ) = 1/√2

El punto es (1/√2, 1/√2)

y – y ₁ = $\frac{dy}{dx}(x-x_1)$

y – (1/√2) = -1(x – 1/√2)

y – 1/√2 = -x + 1/√2

x + y = √2 es la ecuación de la normal es

$y-y_1=\frac{-dx}{dy}(x-x_1)$

y – 1/√2 = 1(x – 1/√2)

x = y es la ecuación de la normal.

Pregunta 15. Encuentra la ecuación de la recta tangente a la curva y = x ² – 2x + 7 que es

(i) Paralelo a la línea 2x – y + 9 = 0

(ii) Perpendicular a la línea 5y – 15x = 13

Solución:

Curva dada: y = x ² – 2x + 7

Al derivar wrt x, obtenemos

dy/dx = 2x – 2 -(1)

(i) La tangente es paralela a 2x – y + 9 = 0, eso significa,

Pendiente de la tangente = pendiente de 2x – y + 9 = 0

y = 2x + 9

Pendiente = 2 -(Comparando con y = mx + e)

dy/dx = pendiente = 2

2x – 2 = 2

x1 = ₂

Correspondiente a x ₁ = 2,

y ₁ = x ₁² – 2x ₁ + 7

y ₁ = (2) ² – 2(2) + 7

y ₁ = 7

El punto de contacto es (2, 7).

Usando la forma de punto pendiente, la ecuación de la tangente es

y – y ₁ = $\frac{dy}{dx}(x-x_1)$

y-7 = 2(x-2)

y – 2x = 3 es la ecuación de la tangente.

(ii) La tangente es perpendicular a la línea 5y – 15x = 13

Eso significa (pendiente de la tangente) x (pendiente de la línea) = -1

Para, pendiente de la línea 5y – 15x = 13

5y = 15x + 13

y = 3x + 13/15

Pendiente = 3

(Pendiente de la tangente) x 3 = -1

Pendiente de la tangente =-1/3

Ahora, y = x ² – 2x + 7

dy/dx = 2x – 2

Al comparar dy/dx con la pendiente, obtenemos

2x – 2 = -1/3

6x – 6 = -1

6x = 5

× ₁ = 5/6

Para x1 = 5/6 _,

y ₁ = x ₁² – 2x ₁ + 7

y ₁ = (5/6) ₁² – 2(5/6) ₁ + 7

_y1 = 217/36

Ahora usando la forma punto pendiente, la ecuación de la tangente es

y – y ₁ = m(x – x ₁ )

$y-\frac{217}{36}=\frac{-1}{3}(x-\frac{5}{6})$

$\frac{36y-217}{36}=-1\frac{(6x-5)}{6.3}$

36y – 217 = -12x + 10

36y + 12x = 227 es la ecuación de tangente requerida.

Pregunta 16. Demuestre que la tangente a la curva y = 7x ³ + 11 en los puntos donde x = 2 y x = -2 son paralelas.

Solución:

Curva dada: y = 7x ³ + 11

Al derivar wrt x, obtenemos

dy/dx = 21x ²

dy/dx = 21(2) ² = 84

Las pendientes en x – 2 y -2 son iguales,

Por tanto, las tangentes serán paralelas entre sí.

Pregunta 17. Encuentra los puntos en la curva y = x ³ en los que la pendiente de la tangente es igual a las coordenadas y del punto.

Solución:

Curva dada: y = x ³

Al derivar wrt x, obtenemos

dy/dx = 3x ² -(1)

Ahora supongamos que el punto es (x ₁ , y ₁ )

dy/dx = 3x ₁²

Además, la pendiente de la tangente en (x1, y1) es igual a y ₁ .

Entonces, 3x ₁² = y ₁ -(2)

Además, (x1, y1) se encuentra en y = x ³ x3, entonces

y ₁ = x ₁³ -(3)

De la ecuación (2) y (3)

3x ₁² = x ₁³

3x ₁² = x ₁³ = 0

x ₁² (3 – x ₁ ) = 0

Para x ₁ = 0, y ₁ = x ₁³ = (0) 3 = 0

Uno de esos puntos es (0, 0)

Para x ₁ = 3, y _1. = (3)3 = 27

El segundo punto es (3, 27)

Pregunta 18. Para la curva y = 4x ³ – 2x ⁵ , encuentre todos los puntos en los que la tangente pasa por el origen.

Solución:

Curva dada: y = 4x ³ – 3x ⁵

Claramente en x = 0, y = 0, es decir, la curva pasa por el origen.

Ahora la tangente también pasa por el origen.

La ecuación de una recta que pasa por el origen es y = mx.

Ahora la tangente toca la curva, entonces

y = mx satisfará en la curva.

mx = 4x ³ – 2x ⁵ -(1)

Ahora dy/dx = 12x ² – 10x ⁴

También m es la pendiente de la tangente, entonces

m = 12x ² – 10x ⁴ -(2)

De la ecuación (1) y (2),

(12x ² – 10x ⁴ )x = 4x ³ – 3x ⁵

x ³ (12 – 10x ² ) = x ³ (4 – 2x ² ) -(3)

Para el primer punto, x = 0

Para x ₁ = 0, y ₁ = 4x ₁³ – 2x ₁⁵ = 0

Entonces, (0, 0) es uno de esos puntos

Ahora para otras raíces de 3

12 – 10x ² = 4 – 2x ²

⁸ = 8×2

× ² = 1

x = ±1

Para x ₂ = 1, y ₂ = 4x ₂³ – 2x ₂⁵ = 4(1) ³ – 2(1) ⁵ = 2

Para x ₃ = -1, y ₃ = 4x ₃³ – 2x ₃⁵ = 4(-1) ³ – 2(-1) ⁵ = -2

Los otros puntos son (1, 2) y (-1, -2)

Pregunta 19. Encuentra los puntos en la curva x ² + y ² – 2x – 3 = 0 en los que las tangentes son paralelas al eje x.

Solución:

Curva dada: x ² + y ² – 2x – 3 = 0

Al derivar wrt x, obtenemos

3x + 2y(dy/dx) – 2 – 0 = 0

$x+y\frac{dy}{dx}=1 \frac{dy}{dx}=\frac{1-x}{y}$

Dado que las tangentes son paralelas al eje x,

Entonces, dy/dx = pendiente = 0

1 – x/y = 0

Para x ₁ = 1,

x ₁² + y ₁² – 2x ₁ – 3 = 0

(1) ² + y ₁² – 2(1) – 3 = 0

y ₁² = 4

y ₁² = ≠2

Los puntos son (1, 2) y (1, -2)

Pregunta 20. Encuentra la ecuación de la normal en el punto (am ² , am ³ ) para la curva ay ² = x ³ .

Solución:

Curva dada: ay ² = x ³

Al derivar wrt x, obtenemos

2ay.dy/dx = 3x ²

$\frac{dy}{dx}=\frac{3x^2}{2ay}$ & $\frac{-dx}{dy}=\frac{-2ay}{3x^2}$

$\frac{-dx}{dy}=\frac{-2a.am^3}{3.(am^2)^2}=\frac{-2}{3m}$

Entonces, por la forma de punto pendiente, la ecuación de la normal es,

$y-y_1=\frac{-dx}{dy}(x-x_1)$

$y-am^3=\frac{-2}{3m}(x-am^2)$

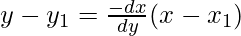
3ma – 3am ⁴ = -2x + 2am ²

Por lo tanto, 3my + 2x = 2am ² + 3am ⁴ es la ecuación requerida de normal.

Pregunta 21. Encuentra la ecuación de las normales a la curva y = x ³ + 2x + 6 que son paralelas a la recta x + 14y + 4 = 0.

Solución:

Curva dada: y = x ³ + 2x + 6

Al derivar wrt x, obtenemos

$\frac{dy}{dx}=3x^2+2$

$\frac{-dx}{dy}=\frac{-1}{3x^2+2}$ -(Pendiente de la normal)

Ahora, las normales son paralelas a x + 14y + 4 = 0

$\frac{-1}{3x^2+2}=\frac{-1}{14}$

13 = 3×2 + ²

3×2 = 12 ⇒x2 ⁼⁴

x = ±2

x1 = 2 y _x2 = _-2

Para x ₁ = 2; y ₁ = $x_1^3+2x_1+6$ = (2) ³ + 2(2) + 6 = 18

Para x2 = -2 _;y ₂ = $x_2^2+2x_2+6$ = (-2) ³ + 2(-2) + 6 = -6

Normal a través de (2,18) es

y-18 = $\frac{-1}{14}(x-2)$

14y – 252 = -x + 2

14y + x = 254 es una de esas ecuaciones.

Normal a (-2, -6) es

y + 6 = $\frac{-1}{14}(x+2)$

14y + 84 = -x – 2

14y + x + 86 = 0 es la otra ecuación de la normal.

Pregunta 22. Halla las ecuaciones de tangente y normal a la parábola y ² = 4ax en el punto (en ² , 2at).

Solución:

Parábola dada: y ² = 4ax

Al derivar wrt x, obtenemos

$2y.\frac{dy}{dx}=4a$

$\frac{dy}{dx}=\frac{2a}{y} ;\frac{-dx}{dy}=\frac{-y}{2a}$

$\frac{dy}{dx}=\frac{2a}{2at}=\frac{1}{t}$

Ahora, por la forma de punto pendiente, la ecuación de la tangente es,

y – y ₁ = $\frac{dy}{dx}(x-x_1)$

$y-2at=\frac{1}{t}(x-at^2)$

ty = x + at ² es la ecuación de la tangente a la parábola y ² = 4ax at (at ² , 2at)

Ahora $\frac{-dx}{dy}=\frac{-2at}{2a}=-t$

Ahora, por la forma de punto pendiente, la ecuación de la normal es,

y – y ₁ = $\frac{-dx}{dy}(x-x_1)$

y – 2 en = -t(x – en ² )

y + xt = 2at + at ³ es la ecuación de la normal a la parábola y ² = 4ax at (at ² , 2at)

Pregunta 23. Demuestra que las curvas x = y ² y xy = k cortan en ángulo recto si 8k ² = 1.

Solución:

Curvas dadas: x = y ² & xy = k

Dos curvas se cortan en ángulos rectos f las tangentes a través de su punto

intersección es perpendicular entre sí.

Ahora bien, si las tangentes son perpendiculares, el producto de sus pendientes será igual a -1.

Curva 1: x = y ²

1 = 2y.dy/dx

dy/dx = 1/2 y = m ₁ -(1)

Curva 2: xy = k

y = k/x

$\frac{-k}{x^2}=m_2$

Encontremos su punto de intersección.

x = y ² y xy = k

k/y = y ²

y = k ^1/3

x = y ²

x = k ^2/3

El punto es (k ^2/3 , k ^1/3 )

m ₁ = 1/2k ^1/3

Para que las curvas se crucen entre sí en ángulo recto,

metro ₁ metro ₂ = -1

$\frac{1}{2k^\frac{1}{3}}.\frac{-1}{k^\frac{1}{3}}=1$

$2k^\frac{2}{3}=1$

8k ² = 1

Por lo tanto probado

Pregunta 24. Encuentra las ecuaciones de la tangente y normal a la hipérbola 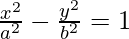$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ en el punto (x _o , y _o ).

Solución:

Curva dada: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

Al derivar ambos lados con respecto a x,

$\frac{2x}{a^2}-\frac{2y}{b^2}.\frac{dy}{dx}=0$

$\frac{dy}{dx}=\frac{xb^2}{ya^2}\&\frac{-dx}{dy}=\frac{-ya^2}{xb^2}$

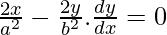
Ahora, $\frac{dy}{dx}=\frac{x_ob^2}{y_0a^2}=m_T$

La ecuación de la tangente por la forma de la pendiente del punto es,

$y-y_1=m_T(x-x_1)$

$y-y_0=\frac{x_0b^2}{y_0a^2}(x-x_0)$

$\frac{yy_0-y_0^2}{b^2}=\frac{xx_0-x_0^2}{a^2}$

$\frac{yy_0}{b^2}-\frac{xx_0}{a^2}=\frac{y_0^2}{a^2}=-1$ -((x ₀ ,y ₀ ) acostarse sobre $\frac{x^2}{a^2}-\frac{b^2}{b^2}=1$ )

$\frac{xx_0}{a^2}-\frac{yy_0}{b^2}=1$ es la ecuación de la tangente.

Ahora, $\frac{-dx}{dy}=\frac{-y_0a^2}{x_0b^2}=m_N$

La ecuación de la normal por punto pendiente es,

$y-y_1=m_N(x-x_1)$

$y-y_0=\frac{-y_0a^2}{x_0b^2}(x-x_0)$

x ₀ segundo ² y – x ₀ segundo ² y ₀ = -y ₀ un ² x + y ₀ un ² x ₀

x ₀ b ² y + y ₀ a ² x = x ₀ y ₀ (a ² + b ² ) es la ecuación de normal

Pregunta 25. Encuentra la ecuación de la tangente a la curva y = 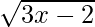$\sqrt{3x-2}$ que es paralela a la recta 4x – 2y + 5 = 0.

Solución:

Curva dada: $y=\sqrt{3x-2}$

Al derivar wrt x, obtenemos

$\frac{dy}{dx}=\frac{1}{2\sqrt{3x-2}}.3$

Ahora, dado que la tangente es paralela a la recta 4x – 2y + 5 = 0,

por lo que sus pendientes deben ser iguales.

La pendiente de 2y = 4x + 5 es 2.

Asi que,

$\frac{dy}{dx}=\frac{3}{2\sqrt{3x-2}}=2$

$\frac{3}{4}=\sqrt{3x-2}$

9/16 = 3x – 2

x1 = _41/48

Ahora, $y_1=\sqrt{3x_1-2}$

$y_1=\sqrt{3.\frac{41}{48}-2}=\frac{3}{4}$

El punto es (41/48, 3/4)

Ahora, por la forma de punto pendiente, la ecuación de la tangente será

y – y ₁ = m(x – x ₁ )

$y-\frac{3}{4}=2(x-\frac{41}{48})$

$y-\frac{3}{4}=2x-\frac{41}{24}$

24y – 48x + 23 = 0 es la ecuación de tangente requerida.

Pregunta 26. La pendiente de la normal a la curva y = 2x ² + 3 sen x en x = 0 es

(A) 3 (B) 1/3 (C)-3 (D) -1/3

Solución:

Curva dada: y = 2x ² + 3 sen x

Al derivar wrt x, obtenemos

dy/dx = 4x + 3cos x

$\frac{-dx}{dy}=\frac{-1}{4x+3\cos x}$ -(Pendiente de la normal)

$\frac{-dx}{dy}=\frac{-1}{4(0)+3\cos 0}=\frac{-1}{3}$

Por lo tanto, la opción correcta es D.

Pregunta 27. La recta y = x + 1 es tangente a la curva y ² = 4x en el punto

(A) (1, 2) (B) (2, 1) (C) (1, -2) (D) (-1, 2)

Solución:

Curva dada: y ² = 4x

Al derivar wrt x, obtenemos

$2y\frac{dy}{dx}=4$

$\frac{dy}{dx}=\frac{2}{y}$

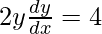
y = x + 1 es tangente, la pendiente es 1, entonces, 2/y = 2

y ₁ = 2,

y ₁² = 4x ₁

x1 = _{_} $\frac{2^2}{4}$

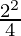
× ₁ = 1

Entonces, (1, 2) es el punto.

Por lo tanto, la opción correcta es A.

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Soluciones NCERT Clase 12 – Matemáticas Parte I – Capítulo 6 Aplicación de Derivadas – Ejercicio 6.3 | conjunto 2

Capítulo 6 Aplicación de Derivadas -Ejercicio 6.3 | Serie 1

Pregunta 14. Encuentra las ecuaciones de la tangente y normal a las curvas dadas en los puntos indicados:

Pregunta 15. Encuentra la ecuación de la recta tangente a la curva y = x ² – 2x + 7 que es

Pregunta 16. Demuestre que la tangente a la curva y = 7x ³ + 11 en los puntos donde x = 2 y x = -2 son paralelas.

Pregunta 17. Encuentra los puntos en la curva y = x ³ en los que la pendiente de la tangente es igual a las coordenadas y del punto.

Pregunta 18. Para la curva y = 4x ³ – 2x ⁵ , encuentre todos los puntos en los que la tangente pasa por el origen.

Pregunta 19. Encuentra los puntos en la curva x ² + y ² – 2x – 3 = 0 en los que las tangentes son paralelas al eje x.

Pregunta 20. Encuentra la ecuación de la normal en el punto (am ² , am ³ ) para la curva ay ² = x ³ .

Pregunta 21. Encuentra la ecuación de las normales a la curva y = x ³ + 2x + 6 que son paralelas a la recta x + 14y + 4 = 0.

Pregunta 22. Halla las ecuaciones de tangente y normal a la parábola y ² = 4ax en el punto (en ² , 2at).

Pregunta 23. Demuestra que las curvas x = y ² y xy = k cortan en ángulo recto si 8k ² = 1.

Pregunta 24. Encuentra las ecuaciones de la tangente y normal a la hipérbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ en el punto (x _o , y _o ).

Pregunta 25. Encuentra la ecuación de la tangente a la curva y = $\sqrt{3x-2}$ que es paralela a la recta 4x – 2y + 5 = 0.

Pregunta 26. La pendiente de la normal a la curva y = 2x ² + 3 sen x en x = 0 es

(A) 3 (B) 1/3 (C)-3 (D) -1/3

Pregunta 27. La recta y = x + 1 es tangente a la curva y ² = 4x en el punto

(A) (1, 2) (B) (2, 1) (C) (1, -2) (D) (-1, 2)

Deja una respuesta Cancelar la respuesta

Capítulo 6 Aplicación de Derivadas -Ejercicio 6.3 | Serie 1

Pregunta 14. Encuentra las ecuaciones de la tangente y normal a las curvas dadas en los puntos indicados:

Pregunta 15. Encuentra la ecuación de la recta tangente a la curva y = x 2 – 2x + 7 que es

Pregunta 16. Demuestre que la tangente a la curva y = 7x 3 + 11 en los puntos donde x = 2 y x = -2 son paralelas.

Pregunta 17. Encuentra los puntos en la curva y = x 3 en los que la pendiente de la tangente es igual a las coordenadas y del punto.

Pregunta 18. Para la curva y = 4x 3 – 2x 5 , encuentre todos los puntos en los que la tangente pasa por el origen.

Pregunta 19. Encuentra los puntos en la curva x 2 + y 2 – 2x – 3 = 0 en los que las tangentes son paralelas al eje x.

Pregunta 20. Encuentra la ecuación de la normal en el punto (am 2 , am 3 ) para la curva ay 2 = x 3 .

Pregunta 21. Encuentra la ecuación de las normales a la curva y = x 3 + 2x + 6 que son paralelas a la recta x + 14y + 4 = 0.

Pregunta 22. Halla las ecuaciones de tangente y normal a la parábola y 2 = 4ax en el punto (en 2 , 2at).

Pregunta 23. Demuestra que las curvas x = y 2 y xy = k cortan en ángulo recto si 8k 2 = 1.

Pregunta 24. Encuentra las ecuaciones de la tangente y normal a la hipérbola en el punto (x o , y o ).

Pregunta 25. Encuentra la ecuación de la tangente a la curva y = que es paralela a la recta 4x – 2y + 5 = 0.

Pregunta 26. La pendiente de la normal a la curva y = 2x 2 + 3 sen x en x = 0 es

(A) 3 (B) 1/3 (C)-3 (D) -1/3

Pregunta 27. La recta y = x + 1 es tangente a la curva y 2 = 4x en el punto

(A) (1, 2) (B) (2, 1) (C) (1, -2) (D) (-1, 2)

Deja una respuesta Cancelar la respuesta

Pregunta 15. Encuentra la ecuación de la recta tangente a la curva y = x ² – 2x + 7 que es

Pregunta 16. Demuestre que la tangente a la curva y = 7x ³ + 11 en los puntos donde x = 2 y x = -2 son paralelas.

Pregunta 17. Encuentra los puntos en la curva y = x ³ en los que la pendiente de la tangente es igual a las coordenadas y del punto.

Pregunta 18. Para la curva y = 4x ³ – 2x ⁵ , encuentre todos los puntos en los que la tangente pasa por el origen.

Pregunta 19. Encuentra los puntos en la curva x ² + y ² – 2x – 3 = 0 en los que las tangentes son paralelas al eje x.

Pregunta 20. Encuentra la ecuación de la normal en el punto (am ² , am ³ ) para la curva ay ² = x ³ .

Pregunta 21. Encuentra la ecuación de las normales a la curva y = x ³ + 2x + 6 que son paralelas a la recta x + 14y + 4 = 0.

Pregunta 22. Halla las ecuaciones de tangente y normal a la parábola y ² = 4ax en el punto (en ² , 2at).

Pregunta 23. Demuestra que las curvas x = y ² y xy = k cortan en ángulo recto si 8k ² = 1.

Pregunta 24. Encuentra las ecuaciones de la tangente y normal a la hipérbola $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ en el punto (x _o , y _o ).

Pregunta 25. Encuentra la ecuación de la tangente a la curva y = $\sqrt{3x-2}$ que es paralela a la recta 4x – 2y + 5 = 0.

Pregunta 26. La pendiente de la normal a la curva y = 2x ² + 3 sen x en x = 0 es

Pregunta 27. La recta y = x + 1 es tangente a la curva y ² = 4x en el punto