Soluciones NCERT Clase 12 – Matemáticas Parte I – Capítulo 6 Aplicación de Derivadas – Ejercicio 6.3

Pregunta 1. Encuentra la pendiente de la tangente a la curva y = 3x ⁴ – 4x en x = 4.

Solución:

Curva dada: y = 3x ⁴ – 4x

Al derivar wrt x, obtenemos

dy/dx = 12x ³ – 4

Ahora, encontramos que la pendiente de la tangente a la curva dada en x = 4 es

= dy/dx = 12(4) ³ – 4 = 764

Por lo tanto, la pendiente es 764

Pregunta 2. Encuentra la pendiente de la tangente a la curva 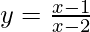$y = \frac{x-1}{x-2}$ , x ≠ 2 en x = 10.

Solución:

Curva dada: $y=\frac{x-1}{x-2}$

$y=\frac{x-2+1}{x-2}=1+\frac{1}{x-2}$

Al derivar wrt x, obtenemos

$\frac{dy}{dx}=0-\frac{1}{(x-2)^2}$

Ahora, encontramos que la pendiente de la tangente a la curva dada en x = 10 es

$\frac{dy}{dx}=\frac{-1}{(10-2)^2}=\frac{-1}{64}$

Por lo tanto, la pendiente es -1/64

Pregunta 3. Encuentra la pendiente de la tangente a la curva y = x ³ – x + 1 en el punto cuya coordenada x es 2.

Solución:

Curva dada: y = x ³ – x + 1

Al derivar wrt x, obtenemos

$\frac{dy}{dx}=\frac{d(x^3-x+1)}{dx}=3x^2-1$

Ahora, encontramos que la pendiente de la tangente a la curva dada en x = 2 es

$\frac{dy}{dx}=3(2)^2-1=11$

Por lo tanto, la pendiente es 11

Pregunta 4. Encuentra la pendiente de la tangente a la curva y = x ³ –3x + 2 en el punto cuya coordenada x es 3.

Solución:

Curva dada: y = x ³ – 3x + 2

Al derivar wrt x, obtenemos

dy/dx = 3x ² – 3

Ahora, encontramos que la pendiente de la tangente a la curva dada en x = 3 es

dy/dx = 3(3) ² – 3 = 24

Por lo tanto, la pendiente es 24

Pregunta 5. Encuentra la pendiente de la normal a la curva x = acos ³ θ, y = asen ³ θ en θ = π/4.

Solución:

Curva dada: x = acos ³ θ = f(θ)

y = asen ³ θ = g(θ)

Para encontrar la pendiente de la normal de la curva en θ = π/4

Ahora, la pendiente de la normal es $\frac{-dx}{dy}$

$\frac{-dx}{dy}=-\frac{\frac{dx}{dθ}}{\frac{dy}{dθ}}$ -(1)

$\frac{dx}{d\theta} =\frac{d(a\cos^3θ) }{dθ}$ = a.3.cos ² θ.(-sen θ)

$\frac{dy}{dθ}=\frac{d(a\sin^3θ)}{dθ}$ = a.3sen ² θ.cos θ

$\frac{-dx}{dθ}=\frac{a.3.\cos^2θ.(-\sinθ)}{a.3.\sin^2θ.\cosθ}$ -(usando la ecuación (1))

$\frac{-dx}{dy}=\frac{\cosθ}{\sinθ}=\cotθ$

Ahora, encontramos que la pendiente de la tangente a la curva dada en θ = π/4 es

$\frac{-dx}{dy}=\cot(\frac{π}{4})=1$

La pendiente de la normal de la curva paramétrica.

Por lo tanto, la pendiente es 1

Pregunta 6. Encuentra la pendiente de la normal a la curva x = 1 – asinθ, y = bcos ² θ en θ = π/2.

Solución:

Curva dada: x = 1 – a senθ

y = b cos2θ

Ahora, la pendiente de la normal es $\frac{-dx}{dy}$

$\frac{-dx}{dy}=\frac{\frac{-dx}{dθ}}{\frac{dy}{dθ}}$ -(1)

$\frac{dx}{dθ}=\frac{d(1-a\sinθ)}{dθ}=-a\cosθ$

$\frac{dy}{dθ}=\frac{d(b\cos^2θ)}{dθ}=-2b\cosθ\sinθ$

$\frac{-dx}{dy}=\frac{-a\cosθ}{-2b\cosθ\sinθ}$ -(usando la ecuación (1))

$\frac{-dx}{dy}=\frac{-a}{2b\sinθ}$

Ahora, encontramos que la pendiente de la tangente a la curva dada en θ = π/2 es

$\frac{-dx}{dy}=\frac{-a}{2b\sin\frac{π}{2}}=\frac{-a}{2b}$

Por lo tanto, la pendiente es -a/2b.

Pregunta 7. Encuentra los puntos en los que la tangente a la curva y = x ³ – 3x ² – 9x + 7 es paralela al eje x.

Solución:

Curva dada: y = x ³ – 3x ² – 9x + 7

Al derivar wrt x, obtenemos

dy/dx = 3x ² – 6x – 9

Para que la tangente sea paralela al eje x, la pendiente es 0. Entonces, dy/dx = 0.

3x ² – 6x – 9 = 0

3(x ² – 2x – 3) = 0

3(x ² + x – 3x – 3) = 0

3(x(x+1) – 3(x+1)) = 0

3(x+1)(x-3) = 0

x = -1 o x = 3

Para x = -1, y = (-1) ³ – 3(-1) ² – 9(-1) + 7

x = -1, y = -1 – 3 + 9 + 7 = 12

Por lo tanto, el primer punto es (-1, 12)

Pregunta 8. Encuentra un punto en la curva y = (x – 2) ² en el que la tangente sea paralela a la cuerda que une los puntos (2, 0) y (4, 4).

Solución:

Curva dada: y = (x – 2) ²

Al derivar wrt x, obtenemos

dy/dx = 2(x – 2) -(1)

Dado que la tangente es paralela a la cuerda que une los puntos (2, 0) y (4, 4)

Pendiente de la cuerda = $\frac{y_2-y_1}{x_2-x_1}=\frac{4-0}{4-2}=\frac{4}{2}=2$

Ahora igualdad dy/dx = pendiente de la cuerda

2(x-2) = 2

x-2 = 1

x = 3

y = (x – 2) ²

y = (3 – 2) ² = 1

Por lo tanto, el punto en la curva y = (x – 2) ² es (3, 1)

Pregunta 9. Encuentra el punto en la curva y = x ³ – 11x + 5 en el que la tangente es y = x – 11.

Solución:

Curva dada: y = x ³ – 11x + 5

Dada la tangente: y = x – 11

De la tangente dada, podemos encontrar la pendiente comparando y = x – 11 con y = mx + c, obtenemos

Pendiente (m) = 1

Ahora y = x ³ – 11x + 5

dy/dx = 3x ² – 11 -(1)

dy/dx = pendiente = 1

Entonces, de la ecuación (1), obtenemos

3x ² – 11 = 1

3×2 ⁼ 12

× ² = 4

x = ±2

Si x = +2, y = 2 ³ – 11(2) + 5 = -9

Si x = -2, y = (-2) ³ – 11(-2) + 5 = 19

Los puntos también deben estar en la tangente.

Solo (2,-9) satisface la ecuación tangente.

Entonces el punto de la curva cuya tangente es y = x – 11 es (2,-9).

Pregunta 10. Encuentra la ecuación de todas las rectas con pendiente –1 que son tangentes a la curva y = 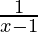$\frac{1}{x-1}$ [Tex] [/Tex], x ≠ 1.

Solución:

Curva dada: y = $\frac{1}{x-1}$

$\frac{dy}{dx}=\frac{-1}{(x-1)^2}$ -(1)

Ahora dada la pendiente = -1 y sabemos que dy/dx = pendiente, entonces

dy/dx = -1 -(1)

De 1 y 2, obtenemos

-1 = $\frac{-1}{(x-1)^2}$

(x-1) ² = 1

x = 1 ± 1

x1 = 2 y _x2 = ₀

Ahora correspondiente a estos x ₁ y x ₂ , necesitamos encontrar y ₁ y y ₂

$y_1=\frac{1}{x-1}=\frac{1}{2-1}=1$

$y_2=\frac{1}{x_2-1}=\frac{1}{0-1}=-1$

Los puntos son (2, 1) y (0, -1)

Ahora la pendiente de las ecuaciones es -1

Usando la pendiente del punto de la primera ecuación tangente es

(y – y ₁ ) = m(x – x ₁ )

y-1 = -1(x-2)

= x + y = 3

Usando la pendiente del punto de la segunda ecuación tangente es

(y – y ₂ ) = m(x – x ₂ )

y-(-1) = -1(x-0)

= x + y + 1 = 0

Pregunta 11. Encuentra la ecuación de todas las rectas con pendiente 2 que son tangentes a la curva 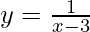$y = \frac{1}{x-3}$ , x ≠ 3.

Solución:

Curva dada: y = 1/(x – 3)

dy/dx = -1/(x – 3) ² = pendiente -(dy/dx es la pendiente)

Ahora la pendiente dada es 2, entonces

dy/dx = -1/(x – 3) ² = 2

(x – 3) ² = -1/2 -(1) (no es posible)

Ahora bien, debido a que no hay un valor real de x que pueda satisfacer 1, no existe tal tangente en la curva y = 1/x – 3 cuya es 2.

Pregunta 12. Encuentra las ecuaciones de las rectas con pendiente 0 que son tangentes a la curva 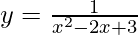$y=\frac{1}{x^2-2x+3}$ .

Solución:

Curva dada,

$y=\frac{1}{x^2-2x+3}$

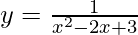
Al derivar wrt x, obtenemos

$\frac{dy}{dx}=\frac{-1}{(x^2-2x+3)}.(2x-2)$ -(string de reglas)

Pendiente dada = 0 = dy/dx

Asi que, $\frac{dy}{dx}=\frac{-2(x-1)}{(x^2-2x+3)^2}=0$

x-1 = 0

X = 1

Para x = 1, y = $\frac{1}{1^2-2(1)+3}=\frac{1}{2}$

Entonces, la ecuación de la tangente desde el punto desde la pendiente es

y – y ₁ = m(x – x ₁ )

$y-\frac{1}{2}$ = 0(x-1)

2 años – 1 = 0

Pregunta 13. Encuentre puntos en la curva 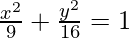$\frac{x^2}{9}+\frac{y^2}{16}=1$ en los que las tangentes son

(i) Paralelo al eje x (ii) Paralelo al eje y

Solución:

Curva dada:

$\frac{x^2}{9}+\frac{y^2}{16}=1$ -(1)

(i) Si la tangente es paralela al eje x, significa que la pendiente es 0 o dy/dx = 0

Al diferenciar ambos lados de la ecuación (1) obtenemos,

$\frac{2x}{9}+\frac{2y}{16}.\frac{dy}{dx}=0$

$\frac{dy}{dx}=\frac{-16x}{9y}$

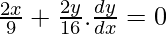
Ahora pendiente = 0, entonces

$\frac{-16x}{9y}=0$

= x ₁ = 0

Para x ₁ = 0,

$\frac{0^2}{9}+\frac{y_1^2}{16}=1$

y ₁² = 16

y1 = ± ₄

Las coordenadas son (0, 4) y (0, -4)

(ii) Ahora, si la tangente es paralela al eje y al dy/dx o la pendiente no está definida o dy/dx = 0

Al diferenciar la ecuación (1) con respecto a y, obtenemos

$\frac{2x}{9}.\frac{dx}{dy}+\frac{2y}{16}=0$

$\frac{dx}{dy}=0,\frac{-9y}{16x}=0$

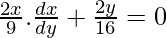
y ₂ = 0

Para y ₂ = 0, $\frac{x_2^2}{9}+\frac{0}{16}=1$

x ₂² = 9

x2 = ± ₃

Por lo tanto, las coordenadas son (3, 0) y (-3, 0)

Capítulo 6 Aplicación de Derivadas -Ejercicio 6.3 | conjunto 2

Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Soluciones NCERT Clase 12 – Matemáticas Parte I – Capítulo 6 Aplicación de Derivadas – Ejercicio 6.3 | Serie 1

Pregunta 1. Encuentra la pendiente de la tangente a la curva y = 3x ⁴ – 4x en x = 4.

Pregunta 2. Encuentra la pendiente de la tangente a la curva $y = \frac{x-1}{x-2}$ , x ≠ 2 en x = 10.

Pregunta 3. Encuentra la pendiente de la tangente a la curva y = x ³ – x + 1 en el punto cuya coordenada x es 2.

Pregunta 4. Encuentra la pendiente de la tangente a la curva y = x ³ –3x + 2 en el punto cuya coordenada x es 3.

Pregunta 5. Encuentra la pendiente de la normal a la curva x = acos ³ θ, y = asen ³ θ en θ = π/4.

Pregunta 6. Encuentra la pendiente de la normal a la curva x = 1 – asinθ, y = bcos ² θ en θ = π/2.

Pregunta 7. Encuentra los puntos en los que la tangente a la curva y = x ³ – 3x ² – 9x + 7 es paralela al eje x.

Pregunta 8. Encuentra un punto en la curva y = (x – 2) ² en el que la tangente sea paralela a la cuerda que une los puntos (2, 0) y (4, 4).

Pregunta 9. Encuentra el punto en la curva y = x ³ – 11x + 5 en el que la tangente es y = x – 11.

Pregunta 10. Encuentra la ecuación de todas las rectas con pendiente –1 que son tangentes a la curva y = $\frac{1}{x-1}$ [Tex] [/Tex], x ≠ 1.

Pregunta 11. Encuentra la ecuación de todas las rectas con pendiente 2 que son tangentes a la curva $y = \frac{1}{x-3}$ , x ≠ 3.

Pregunta 12. Encuentra las ecuaciones de las rectas con pendiente 0 que son tangentes a la curva $y=\frac{1}{x^2-2x+3}$ .

Pregunta 13. Encuentre puntos en la curva $\frac{x^2}{9}+\frac{y^2}{16}=1$ en los que las tangentes son

(i) Paralelo al eje x (ii) Paralelo al eje y

Capítulo 6 Aplicación de Derivadas -Ejercicio 6.3 | conjunto 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la pendiente de la tangente a la curva y = 3x 4 – 4x en x = 4.

Pregunta 2. Encuentra la pendiente de la tangente a la curva , x ≠ 2 en x = 10.

Pregunta 3. Encuentra la pendiente de la tangente a la curva y = x 3 – x + 1 en el punto cuya coordenada x es 2.

Pregunta 4. Encuentra la pendiente de la tangente a la curva y = x 3 –3x + 2 en el punto cuya coordenada x es 3.

Pregunta 5. Encuentra la pendiente de la normal a la curva x = acos 3 θ, y = asen 3 θ en θ = π/4.

Pregunta 6. Encuentra la pendiente de la normal a la curva x = 1 – asinθ, y = bcos 2 θ en θ = π/2.

Pregunta 7. Encuentra los puntos en los que la tangente a la curva y = x 3 – 3x 2 – 9x + 7 es paralela al eje x.

Pregunta 8. Encuentra un punto en la curva y = (x – 2) 2 en el que la tangente sea paralela a la cuerda que une los puntos (2, 0) y (4, 4).

Pregunta 9. Encuentra el punto en la curva y = x 3 – 11x + 5 en el que la tangente es y = x – 11.

Pregunta 10. Encuentra la ecuación de todas las rectas con pendiente –1 que son tangentes a la curva y = [Tex] [/Tex], x ≠ 1.

Pregunta 11. Encuentra la ecuación de todas las rectas con pendiente 2 que son tangentes a la curva , x ≠ 3.

Pregunta 12. Encuentra las ecuaciones de las rectas con pendiente 0 que son tangentes a la curva .

Pregunta 13. Encuentre puntos en la curva en los que las tangentes son

(i) Paralelo al eje x (ii) Paralelo al eje y

Capítulo 6 Aplicación de Derivadas -Ejercicio 6.3 | conjunto 2

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la pendiente de la tangente a la curva y = 3x ⁴ – 4x en x = 4.

Pregunta 2. Encuentra la pendiente de la tangente a la curva $y = \frac{x-1}{x-2}$ , x ≠ 2 en x = 10.

Pregunta 3. Encuentra la pendiente de la tangente a la curva y = x ³ – x + 1 en el punto cuya coordenada x es 2.

Pregunta 4. Encuentra la pendiente de la tangente a la curva y = x ³ –3x + 2 en el punto cuya coordenada x es 3.

Pregunta 5. Encuentra la pendiente de la normal a la curva x = acos ³ θ, y = asen ³ θ en θ = π/4.

Pregunta 6. Encuentra la pendiente de la normal a la curva x = 1 – asinθ, y = bcos ² θ en θ = π/2.

Pregunta 7. Encuentra los puntos en los que la tangente a la curva y = x ³ – 3x ² – 9x + 7 es paralela al eje x.

Pregunta 8. Encuentra un punto en la curva y = (x – 2) ² en el que la tangente sea paralela a la cuerda que une los puntos (2, 0) y (4, 4).

Pregunta 9. Encuentra el punto en la curva y = x ³ – 11x + 5 en el que la tangente es y = x – 11.

Pregunta 10. Encuentra la ecuación de todas las rectas con pendiente –1 que son tangentes a la curva y = $\frac{1}{x-1}$ [Tex] [/Tex], x ≠ 1.

Pregunta 11. Encuentra la ecuación de todas las rectas con pendiente 2 que son tangentes a la curva $y = \frac{1}{x-3}$ , x ≠ 3.

Pregunta 12. Encuentra las ecuaciones de las rectas con pendiente 0 que son tangentes a la curva $y=\frac{1}{x^2-2x+3}$ .

Pregunta 13. Encuentre puntos en la curva $\frac{x^2}{9}+\frac{y^2}{16}=1$ en los que las tangentes son