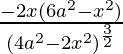Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 6 Aplicación de Derivadas – Ejercicio 6.5 | conjunto 2

Pregunta 13. Encuentra dos números cuya suma sea 24 y cuyo producto sea lo más grande posible.

Solución:

Supongamos dos números x e y.

Dado que x + y = 24 ⇒ y = 24 – x

Ahora tomemos una función producto P(x) = xy

Ahora pon el valor de y

P(x) = x.(24 – x)

P(x) = 24x – ^x2

Ahora, tenemos que maximizar nuestro producto P(x).

Derivando P(x) con respecto a x, obtenemos,  

Ahora pon P'(x)=0

24 – 2x = 0

X = 12

y = 24 – x = 24-12

y = 12

Por lo tanto, los dos números son 12 y 12 y el producto máximo es 144.

Pregunta 14. Encuentra dos números positivos x e y tales que x + y = 60 y xy ³ sea máximo.

Solución:

Dado que, 

x + y = 60 ⇒ x = 60 – y, x > 0, y > 0

Tomemos una función P(y) = xy ³

P(x) = (60 – y)y ³

P(x) = 60y ³ – y ⁹

Al diferenciar P(y) con respecto a y, obtenemos

P'(y) = 180y ² – 4y ³

Ahora pon P'(y) = 0

180y ² – 4y ³ = 0

4y ² (45 – y) = 0

y = 0 o y = 45

No aceptamos y = 0 porque y > 0

Entonces, y = 45

x = 60 – y = 60 – 45

X = 15

Pregunta 15. Encuentra dos números positivos x e y tales que su suma sea 35 y el producto x ² y ⁵ sea un máximo.

Solución:

Dado que,

x + y = 35 ⇒ y = 35 – x 

Consideremos P(y) = x ² y ⁵  

Ponga el valor de y de la ecuación anterior

P(x) = x2 ⁽ 35 – x) ⁵

Al diferenciar P(x) con respecto a y, obtenemos,

P'(x) = x ² 5(35 – x) ⁴ (-1) +(35 – x) ⁵ 2x

P'(y) = x(35 – x) ⁴ [-5x + (35 -x)2]

P'(y) = 7x(35 – x) ⁴ (10 – x)

Ahora pon P'(x) = 0

7x(35 – x) ⁴ (10 – x) = 0

x = 0 o x = 35 o x = 10

Aquí, x = 0 se rechaza porque x es positivo, x = 35 también se rechaza porque 

y = 35 – 35 = 0, pero y es positivo. Entonces, x = 10 es el punto de inflexión.

Ahora hacemos la prueba de la segunda derivada

P”(x) = 7(35 – x) ³ (6x ² – 120x +350)

Ahora pon x = 10

obtenemos

P”(x) = 7(35 – 10) ³ (6 x 100 – 120 x 10 +350)

= 7(25) ³ (250) < 0

Entonces, por la prueba de la segunda derivada, p'(x) será máximo en x = 10. Entonces, y = 25

Pregunta 16. Encuentra dos números positivos cuya suma sea 61 y la suma de cuyos cubos sea mínima.

Solución:

Consideremos dos números a e y

x + y = 16 ⇒ y = 16 – x

Suma de cubos = x ³ + y ³ 

Así que consideremos s(x) = x ³ + y ³ 

S(x) = x ³ + (16 – x) ³

S(x) = x3 ⁺ 163 – ^{x3 – 3.16.x( 16} – x )

S(x) = 16 ³ – x.16 ² .3 + 3.16.x ²

S'(x) = 2.3.16x – 3.16 ²

Ahora pon S'(x) = 0

2.3.16.x = 3.16 ²

2x = 16

x = 8

Entonces, en x = 8 S”(x) = 96 (positivo), entonces x = 8 es un punto mínimo local. Por eso

y = 16 – x = 8

Los dos números son 8 y 8 y la suma de los cubos es 8 ³ + 8 ³ = 1024

Pregunta 17. Una pieza cuadrada de hojalata de 18 cm de lado se va a convertir en una caja sin tapa, cortando un cuadrado de cada esquina y doblando las solapas para formar la caja. ¿Cuál debe ser el lado del cuadrado a cortar para que el volumen de la caja sea el máximo posible?

Solución:

El cuadrado punteado será la base del paralelepípedo abierto.

El lado será 18 – 2x

El cuboide ahora tendrá dimensiones 18 – 2x, 18 – 2x, x

Volumen de la caja abierta,

V(x) = (18 – 2x).(18 – 2x).x

V(x) = x(18 – 2x) ²

Ahora tenemos que maximizar V(x),

Ahora pon V'(x) = 0

V'(x) = 2(18 – 2x).x(-2) + (18 – 2x) ² = 0

(18 – 2x)[-4x + 18 – 2x] = 0

(18 – 2x)(18 – 6x) = 0

x = 9 y x = 3

Ahora pon x = 9

V(x) = (18 – 2x) ² .x

V(9) = (18 – 2 x 9 ⁾ 2,9

V(9) = 0

Es imposible por lo que no aceptamos x = 9

Ahora pon x = 3

V(x) = (18 – 2x) ² .x

V(3) = (18 – 2 x 3) ² .3

V(3) = 432

Entonces, x = 9 es el punto de inflexión

Por lo tanto, en x = 9, V”(x) = -72 (negativo), por lo tanto, el volumen es mínimo en x = 3. 

Ahora, los lados del cuadrado para el volumen máximo son 3.   

Pregunta 18. Una lámina rectangular de hojalata de 45 cm por 24 cm se va a convertir en una caja sin tapa, cortando cada esquina en forma cuadrada y doblando las solapas. ¿Cuál debe ser el lado del cuadrado a cortar para que el volumen de la caja sea máximo? 

Solución:

Dado,

Una lámina rectangular de dimensión 45 x 24. Sea x el lado del cuadrado de la pared,

Entonces el paralelepípedo tiene como base el rectángulo azul y altura igual al lado del cuadrado.

Las dimensiones del paralelepípedo serán 45 – 2x, 24 – 2x y x.

Sea V(x) = función de volumen, entonces

V(x) = (45 – 2x)(24 – 2x)(x)

V(x) = (45x – 2x ² )(24 – 2x)

V'(x) = (45x – 2x ² )(-2) + (24 – 2x)(45 – 4x)

Ahora pon V'(x) = 0

(45x – 2x ² ).2 = 2(12 – x)(45 – 4x)

45x – 4x ² = 12,45 – 48x – 45x + 4x ²

6x ² – 138x + 12,45 = 0

x ² – 23x + 90 = 0

(x-18)(x-5) = 0

x = 18 o x = 5

x no puede ser igual a 18, 24 – 2x se volverá negativo. Por lo tanto, x = 5 es el punto de inflexión. 

Ahora, el volumen es V(x) = (45 – 2x)(24 – 2x)(x)

Ahora pon x = 5, V = (45 – 10).(24 – 10).(5)

V = 35.12.5

V = 2100

El lado del cuadrado pequeño mide 5 cm.

Pregunta 19. Muestre que de todos los rectángulos inscritos en un círculo fijo dado, el cuadrado tiene el área máxima.

Solución:

Dado, un rectángulo variable dentro de un círculo fijo.

Sea el diámetro del círculo fijo igual a d y el 

los lados del rectángulo sean iguales a x e y 

Ahora, el diámetro d es fijo.

Sea la función de área A(x) = xy

Del triángulo ABC,

AB ² + BC ² = AC ²

x ² + y ² = (2a) ²

y ² = (2a) ² – x ²

y = 

Ahora, A(x) = xy = x.

A'(x) = x.

A'(x) = 

ahora hallamos la segunda derivada

A”(x) = 

Ahora ponga A'(x) = 0 para valores máximos y mínimos.

A'(x) =   = 0

x = √2a

Cuando x = √2a,   = -4(negativo)

Entonces, en x = √2a el área del rectángulo es máxima, por lo tanto, y = √2a 

Pregunta 20. Demostrar que el cilindro circular recto de superficie dada y volumen máximo es tal que su altura es igual al diámetro de la base.

Solución:

Dado,

Un cilindro circular recto de área de superficie dada.

Ahora, sea la superficie total A.

A = 2πr(r + h)

A/2π = r ² + rh

Supongamos A/2π = M

h = M – r ² /r

Ahora el volumen del cilindro V(r) = πr ² h

Entonces, V(r) = πr ² (M – r ² /r)

= π(rM – ^r3 )

V'(r) = π(M – 3r ² )

y V”(r) = -π(6r)

Ahora pon V'(r) = 0

π(rM – r3 ⁾ =0

r = √M/3

En r = √M/3, V”(r) = -π(6√M/3) es negativo, por lo que r es máximo en √M/3. 

Por lo tanto, h = 2r

Claramente, la altura es igual al diámetro de la base.

Pregunta 21. De todas las latas cilíndricas (circulares rectas) cerradas, de un volumen dado de 100 centímetros cúbicos, ¿cuáles son las dimensiones de la lata que tiene la superficie máxima? 

Solución:

Dado: lata cilíndrica de volumen fijo = 100 cc.

Encuentra: las dimensiones de la lata 

Como sabemos que

Volumen = πr ² h = 100cc

h = 100/πr ²             ————-(1)

Ahora, el área de superficie total (A) = 2πr ² + 2πrh

A = 2πr ² + 2πr(100/πr ² )

A = 2πr ² + (200/r)

A'(r) = 4πr+ (200/r ² )

ahora encontramos

A”(r) = 4π+ (200/r ³ )

Ahora pon A'(r) = 0

A'(r) = 4πr+ (200/r ² ) = 0

r = (50/π) ^1/3

En r = (50/π) ^1/3 , A”(r) = 4π+ (200/((50/π) ^1/3 ) ³ ) = 12π es positivo. 

Entonces, el área es mínima cuando r = (50/π) ^1/3 .

Por lo tanto, la altura es (h) = 100/π((50/π) ^1/3 ) ² = 2.(50/π) ^1/3 = 2r

Pregunta 22. Un alambre de 28 m de largo debe cortarse en dos pedazos. Una de las piezas se va a convertir en un cuadrado y la otra en un círculo. ¿Cuál debe ser la longitud de las dos piezas para que el área combinada del cuadrado y el círculo sea mínima?

Solución:

Dado que la longitud del alambre es de 8 y se corta en dos pedazos. De uno 

De una pieza se forma un cuadrado y de otra pieza se forma un círculo. Entonces deja 

Supongamos que x es el lado del cuadrado y y el radio del círculo. 

Entonces, Longitud del cable = Perímetro (del cuadrado) + circunferencia (del círculo)

28 = 4x + 2πy

y = (14 – 2x)/π

Como sabemos que el área del círculo es πy ² y el área del cuadrado es x ²

Entonces, área total (A) = πy ² + x ²

Ahora ponemos el valor de y obtenemos

A = π((14 – 2x)/π) ² + x ²

A'(x) = 2x – 8/π(7 – x)

y 

A”(x) = 2 + 8/π

Ahora pon A'(x) = 0

2x – 8/π(7 – x) = 0

x = 28/π + 4

Entonces, en el punto x = 28/π + 4, el área es mínima porque A”(x) es positiva. 

Por lo tanto, el alambre cortado a la distancia 28/π + 4 

Pregunta 23. Demostrar que el volumen del cono más grande que se puede inscribir en una esfera de radio R es 8/27 del volumen de la esfera.

Solución:

Según la pregunta se da que la esfera contiene un cono. 

Así que supongamos que el centro de la esfera es O, el radio de la esfera es R y UV = x y SV = y.

Entonces en el triangulo OVU

OV ² + VU ² = OU ²

(y – R) ² + x ² = R ²

x2 = 2Ry – y2 ^… (1 ⁾

Entonces, el volumen del cono(V) = 1/3πx ² y

Ahora pon el valor de x de eq(1)

= 1/3π(2Ry – y ² )y

V = 1/3π(2Ry ² – y ³ )

V'(y) = 1/3π(4Ry – 3y ² )

y 

V”(y) = 1/3π(4R – 6y)

Ahora pon V'(y) = 0

1/3π(4Ry – 3y ² ) = 0

y = 4R/3

Entonces, en y = 4R/3, V”(y) = 1/3π(4R – 6y) = 1/3π(4R – 6(4R/3)) = -4R/3 es negativo. 

Entonces, el volumen es máximo en y = 4R/3.

Ahora pon el valor de y en la ecuación (1), obtenemos

x2 ⁼ 2R(4R/3) – (4R/3) ² 

x = 8R ² /9

Entonces el volumen máximo del cono es 

V = 1/3πx ² y

V = 1/3π(8R ² /9) ² (4R/3) = 8/27

Pregunta 24. Muestre que el cono circular recto de superficie menos curva y volumen dado tiene una altura igual a √2 veces el radio de la base.

Solución:

Consideremos r el radio del cono y h la altura del cono.

Entonces, el volumen del cono(V) = 1/3πr ² h

r ² h = 3V/π

r2 ⁼ M/h [3V/π = M] ….(1)

Como sabemos que el área de la superficie del cono:

(A) = 

(A) ² = π ² r ² (r ² + h ² )

Ahora pon el valor de r ² desde arriba

(A) ² = S = π ² M/h (M/h + h ² )

= π ² M(M/h ² + h)

Entonces, S'(h) = π ² M(-2Mh ^-3 + 1) y

S”(h) = π ² M(6Mh ^-4 ) 

Ahora pon S'(h) = 0

π ² M(-2Mh ^-3 + 1) = 0

h = (2M) ^1/3

Entonces en h = (2M) ^1/3 , S”(h) = π ² M(6Mh ^-4 ) = 6π ² M ² /(2M) ^4/3 es positivo. 

Entonces, el área es mínima en h = (2M) ^1/3

Entonces, r = M/(2M) ^1/3

De la ecuación (1), obtenemos

h = √2r

Pregunta 25. Demuestre que el ángulo semivertical del cono de volumen máximo y de altura inclinada dada es tan ^-1 √2.

Solución:

Supongamos que r es el radio, h la altura, l la altura inclinada y θ el ángulo semivertical del cono. 

Asi que, 

l ² = r ² + h ²

r ² = l ² – h ²  ….(1)

Como sabemos que el volumen del cono es 

V = 1/3πr ² h

Ahora ponga el valor de r ² de eq(1)

V = 1/3π(l ² – h ² )h

V = 1/3π(hl ² – h ³ )

Entonces, V'(h) = 1/3π(l ² – 3h ² ) y 

V”(h) = 1/3π(- 6h) = -2πh

Ahora pon V'(h) = 0

1/3π(l ² – 3h ² ) = 0

h = l/√3

Entonces, en h = l/√3, V”(h) = -2πh = -2π(l/√3) es negativo, entonces, V es máximo en h = l/√3

Entonces de la ecuación (1), obtenemos

r2 = l2 ^{– (l /} √3) ²

r= √2(l/√3)

Como sabemos que el ángulo semivertical es tan θ = r/h = √2(l/√3)/l/√3 = √2. Entonces el valor de θ = tan ^-1 √2

Pregunta 26. Muestre que el ángulo semi-vertical del cono circular recto de área de superficie dada y volumen máximo es sen ^-1 (1/3).

Solución:

Supongamos que r es el radio, h la altura y θ el ángulo semivertical del cono. 

Entonces, el área de superficie total (A) = 

= A/π

= S

 = S – r ²

Al cuadrar en ambos lados obtenemos

r ² (r ² + h ² ) = (S – r ² ) ²

r ² = S ² /h ² + 2S ² ….(1)

Como sabemos que el volumen del cono es 

V = 1/3πr ² h

Ahora pon el valor de r, obtenemos

V = 1/3π(S ² /h ² + 2S ² )h

V = 1/3πS ² (h/h ² + 2S)

Ahora 

V'(h) = 1/3πS ² (2S – h ² )/(h + 2S) ²

Ahora pon V'(h) = 0

 1/3πS ² (2S – h ² )/(h + 2S) ² = 0

h = +-√2S

Aquí, h = √2S es un valor válido y h = -√2S no es válido porque la altura no puede ser negativa. Entonces, h = √2S es el punto de inflexión. 

V'(h) > 0, por lo que el volumen es máximo en h = √2S. 

Así que pon el valor de h = √2S en la ecuación (1), obtenemos

r = √S/2

y como sabemos que el ángulo semivertical es sen θ = r/√r ² + h ² . Entonces el valor de θ = tan ^-1 1/3

Pregunta 27. El punto de la curva x ² = 2y que está más cerca del punto (0,5) es 

(A)(2, √2, 4) (B) (2, √2, 0) (C) (0, 0) (D) (2, 2)

Solución:

Dado que, x ² = 2y

Sea cualquier punto aleatorio en esta curva (h, k)

Entonces, h ² = 2k; k = hora ² /2

El punto aleatorio es (h, h ² /2)

Minimizando la distancia

re ² = (h – 0) ² + ( ) 

re ² = f(x) = h ² + 

f'(x) = 2h + 2 .h

Ahora pon f'(h) = 0

2h[1+ ] = 0

h = 0 o 

h = 0  o  h = 2√2​,  h =−2√2

Si h = 0, d=

Si h = ±2√2,

Entonces, h = ±2√2 [dando la distancia mínima]

k = h2/2 = 8/2 = 4

Los puntos son (±2√2, 4)

Entonces la opción correcta es A

Pregunta 28. Para todos los valores reales de x, el valor mínimo de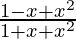

(A) 0 (B)1 (C)3 (D)1/3

Solución:

Dado que, 

 Ahora pon f'(x) = 0

1 + x + x ² – 2x ² – x = 0

× ² = 1

x = ±1 

Entonces, x = -1, x = 1 son los puntos de inflexión

Ahora encontremos el valor de f(x) en los puntos x = -1, x = 1

Pon x = 1

f(1) = 1/3

Pon x = -1

f(-1) = 3

Por lo tanto, el valor máximo de   es 1/3

Entonces la opción correcta es D

Pregunta 29. El valor máximo de [x(x – 1) + 1] ^1/3 , 0 ≤ x ≤ 1 es 

(A) (1/3) ^1/3                    (B) 1/2 (C) 1 (D) 0

Solución:

Dado que,

f(x) = [x(x – 1) + 1] ^1/3 = (x ² – x + 1) ^1/3 , x ϵ [0, 1]

f ′( x ) = 1/3​( x ² − x + 1) ^-2/3 ​.(2 x −1)

o podemos escribir como

 

Ahora pon f'(x) = 0

2x – 1 = 0

Entonces, x = 1/2 es el punto de inflexión que pertenece al intervalo cerrado dado 0 ≤ x ≤ 1. 

Ahora busquemos el valor de f(x) en los puntos x = 1/2, x = 0, x = 1

Pon x = 1/2

f(1/2) = (1/4 – 1/2 + 1) ^1/3

f(1/2) = (3/4) ^1/3 < 1

Pon x = 1

f(1) = (1 – 1 + 1) ^1/3

f(1) = 1

Pon x = 0

f(0) = (0 – 0 + 1) ^1/3

f(0) = 1

Por lo tanto, el valor máximo de [x(x – 1) + 1] ^1/3 es 1

Entonces la opción correcta es C